神经网络自适应PID控制及其应用

神经网络自适应PID控制及其应用

总结来自重庆大学宋永瑞教授2022暑期校园行学术会议

1. 研究背景

  目前人工智能的发展为很多领域里的研究提供了可延展性，提供了新的研究问题的思路，无人系统和人工智能正走向深度融合，无人系统里具有核心驱动作用的智能控制算法的研究成为了热点问题。
人工智能的理论深度依赖人工神经网络，而人工神经网络又是人工智能的核心支撑，先进的控制系统实现了可靠的无人系统的底层支撑，当人工智能与无人系统深度融合时，可以使得实现一个可信、可靠、通用、普适的神经网络驱动的控制系统变得具有很强的可行性，所以，智能无人系统的一个热点就是聚焦于神经网络驱动的控制系统功效性及可靠性的研究。

2. PID

2.1 PID控制器系统简介

  PID算法是控制工程中的一种经典控制理论，其在控制系统中作用效果明显，适用范围广，在目前的实际工程应用中仍然是一种影响力最大适用最多的控制系统。

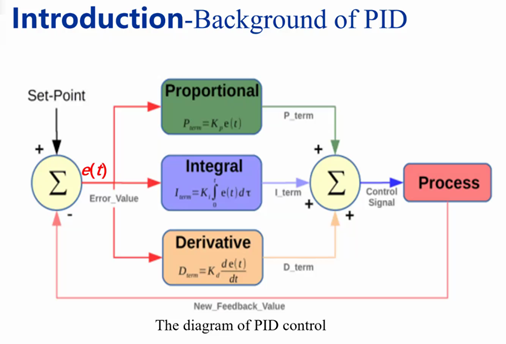
  PID控制器中的P指的是Proportional，即比例，反映参数为比例因子，是对输入到目标趋近速度影响最大的因子，其线性控制系统的驱动；I指的是Integral，即积分，反映参数为积分因子，是对于误差的累计，从而根据之前的误差来修正本次误差的修正；D指的是Derivative，即微分，反映参数为微分系数，是对于抑制误差的修正，防止过度修正和稳态误差的形成。

2.2 PID对于人类智慧的类比

  PID控制器的系统中其实蕴含了“人类智能”，实际表现为人类社会的行事纠正约束准则在系统调节中的适用，$P_{term}=K_{p}e(t)$为比例部分的调节描述，$K_p$为比例系数，确定参数后，系统将会根据输入与目标差值相关的误差，进行按照比例系数线性调节系统，使得系统能够快速的接近目标值，这部分的调节类似于人类的奖惩机制，当误差大时，比例参数的作用就会大，系统变动大，当误差小时，比例参数的作用相对会小，对系统的调整输入量就会变小一些，当误差为正值的时候，其修正量为正继续修正，当误差为负值时，系统的修正量就要为负值，适当拉回过度修正的表现值，当系统误差为0时则比例部分不会做修正；当$I_{term}=K_i{\int }_0^{t}e(t)dt$为积分部分的调节描述，$K_i$为积分系数，此部分将每次的误差进行累计，在积分部分，此前系统的每一次误差都对系统有贡献，积分项蕴含了人类的记忆、经验、总结的机制，对之前所修正的每一次输入的误差都进行了考量，从而防止了稳态误差的出现，累加误差的过程就是吸取经验和教训的过程；$D_{term}=K_d\frac{d_{e(t)}}{d_t}$为微分项部分的调节描述，$K_d$为微分系数，此部分将对误差进行微分，以此来根据误差的变化趋势进行适当的修正，微分部分的蕴含了未来信息、预测机制，一定程度上可以防止过度修正情况的发生。
综上所述，一个PID控制器就是一个人类奖惩+记忆（经验）+预测（预判）运用在控制系统中的典范。

2.3 PID的当前存在的局限

1. PID参数总是常量，从一开始设置之后就不会变动，在整个系统的运行过程中都会保持不变，这在应付复杂多变的工业系统环境时略显局限。
2. PID的参数的设置往往是在大量的实验过程中确定的，效果表现良好达到要求时才会确定，这个确定参数的过程是很痛苦且耗费时间的。
3. PID在非线性系统中的应用效果不明显，具有模糊性。
4. 对于闭环系统缺乏理论上的保证。
   这几点体现在了灵活性、鲁棒性、适应性和其他的表现上。

3. 基于神经网络的自适应PID的设计

3.1 可信、可靠、可解释的PID

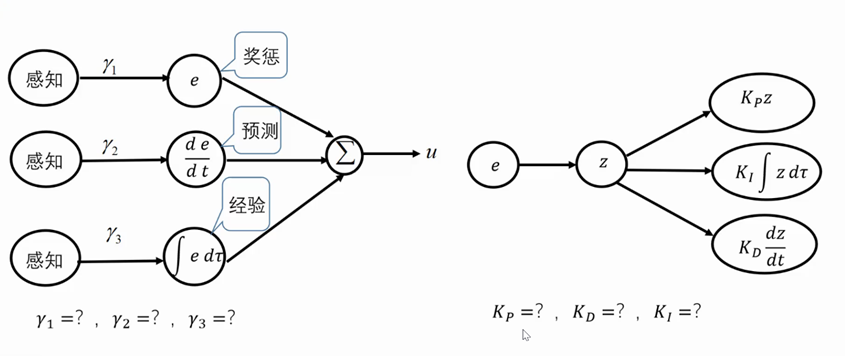
  一个PID的作用描述架构图如下所示。系统通过外部的感知得到输入数据，通过确定系数${\gamma }_1$、${\gamma }_2$、${\gamma }_3$来得到奖惩、预测、经验的分量，加权求和后形成输出$u$，而误差$e$的运作机制往往不是单纯的计算输入与目标的差值，而是使用一种加权的形式进行重映射，这样做也更合理一些，将误差$e$映射输出为z之后，利用确定好的比例系数、积分系数、微分系数，来对系统进行调节。

3.2 稳定性分析

  在控制原理中对于系统出错的处理有个经典的理论，$u_a\left(t\right)=\rho \left(t\right)u+\epsilon (t)$，其中$u=[u_1,\dots ,u_l]\in Rl$为设计的输入，$\epsilon =[{\epsilon }_1,\dots ,{\epsilon }_l]\in Rl$为不可控部分， ρ = d i a g { ρ j } ϵ R l × l , j = 1 , … , l \rho=diag\left\{\rho_j\right\}\epsilon R^{l\times l},j=1,\ldots,l ρ=diag{ ρj​}ϵRl×l,j=1,…,l，为健康指示，当${\rho }_i(t)$为1且$\epsilon (t)$为0时，系统处于正常的执行器；当${\rho }_i(t)$小于1且$\epsilon (t)$为0时，系统会损失一些有效性；当${\rho }_i(t)$小于1且$\epsilon (t)$为常量时，系统能够在突发情况发生时进行适当的修正；当${\rho }_i(t)$小于1且$\epsilon (t)$为随时间变化的量时，系统在突发故障发生时将会失去有效性。

  一般$\rho$不为1的情况反应如下

  一般$\epsilon$不为0的信号反应如下

3.3 误差滤波处理

  系统的实际误差定义为$e_i={x_l}^{(i-1)}-y^{\ast \left(i-1\right)},i=1,\dots ,n$，对误差进行加权求和，即引入滤波误差$z(t)$，$z\left(t\right)={\lambda }_{n-2}{e}_1+\dots +{\lambda }_1{e}_{n-2}+e_{n-1}\Leftarrow (x,\dots ,x^{(n-2)})，\dot{z}\left(t\right)={\lambda }_{n-2}{e}_2+\dots +{\lambda }_1{e}_{n-1}+e_n\Leftarrow (x,\dot{x},\dots ,x^{(n-1)})$，两者为导数关系，经过1991年Slotine和Li的论文验证，当$z\left(t\right)，z(t)\in l\infty$时，$e_1,\dots .,e_n\in {\ell }_{\infty }$，也即滤波后的$z(t)$最小时$e(t)$也最小，所以误差的问题研究滤波后的误差更具有代表性和可行性。
由于我们的目标是设计一个自适应的容错的PID控制器来获得$z(t)$和$\dot{z}(t)$，使其确保所有的闭环系统的信号达到边界，生成最小的残差集。将系统中所有的不可控因素都添加进来，得到了$\ddot{z}(t)$，如下所示

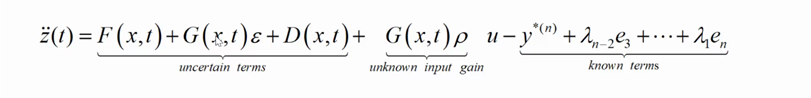
  其第一部分为不确定项，第二部分为未知的生成输入，第三部分为已知项，通过标准化误差z函数，获得以下公式如下

  所讨论的系统应当分为两类，一类是方系统，一类是非线性的非方系统，方系统指的是输入个数与输出个数相同的系统，反之，非方系统指的就是输入与输出不同的系统，一般方系统的分析较为标准，解决方法灵活，对于控制系数矩阵，其正定性决定了控制系统的走向，正定矩阵代表着系统要朝增强的方向输出信号，负定则代表着系统要朝着反向进行输出信号。
引入一般化的误差$e(t)$，即$z\left(t\right)={\lambda }_{n-2}{e}_1+\dots +{\lambda }_1{e}_{n-2}+e_{n-1}\Leftarrow (x,\dots ,x^{(n-2)})$，对其进行再次滤波，可得到

$$E=2\gamma z+{\gamma }^2{\int }_0^{t}z\left(\bullet \right)d\tau +\frac{dz}{dt}$$
  那么整个建模的设计思路就是通过$E$反映了$z$，而$z$反映了$e$，将E最小化是我们的目标。
设$L$为所有不确定因素的综合，不确定因素包括系统的抖动、故障、人为因素、环境因素等等，而对于不确定因素的处理是整个系统设计最困难的部分，目前的处理方法有三种：

1. 参数分解法：$L\left(x\right)=\psi p$，其中$p$为未知参数向量，$\psi$为已知的矩阵函数（回归算子），这种处理方式的解是理想的解，但是处理过程和执行难度复杂，且通常不可分解。
2. 提取核函数$\left|\left|L\left(x\right)\right|\right|\le \psi ,p\ge 0$为未知参数向量，$\psi \ge 0$为已知的光滑函数，此方式基于本质信息且易于实现，缺点是效果不明显容易受扰动。
3. 采用神经网络（NN）逼近，此种方式为与人工智能神经网络结合解决问题的典型思路，思路来源为万能逼近定理，但是运用此定理解决问题的数据集是有条件的，要求数据必须是同一紧集，处理数据时可以采用引入约束的方式规范数据为同一紧集，第二个就是被逼近的函数本身是要连续光滑的，第三个点就是神经元的数目，神经元的数目决定了网络的复杂性，对于神经元的数据和网络的复杂程度的问题，只能在实验中去迭代发现，具体可以在一开始设置一个合理的数目，然后引入神经元数目的增减机制，这个增减机制在生物学上是有理可据的，其与生物的细胞凋亡与生长是完全吻合的。

3.4 控制器的设计

  经过引入滤波后的误差，可以进行PID控制器的设计，PID的建模设计如下：
$$u=\left(k_p+\Delta k_p\left(\bullet \right)\right)z+\left(k_l+\Delta k_l\left(\bullet \right)\right){\int }_0^{t}zd\tau +{(k}_D+\Delta k_D\left(\bullet \right))\frac{dz}{dt}$$
  这样设计之后，原本的PID的参数由Kp（比例系数）、Ki（积分系数）、Kd（微分系数）三个变为了$k_p$、$\Delta kp$∙、$kl$、$\Delta kl$∙、$kD$、$\Delta kD$∙六个参数，三个常量参数$k_p$、$kl$、$kD$以及三个随时间变化的参数$\Delta k_p\left(\bullet \right)$、$\Delta kl$∙、$\Delta kD$∙，但是经过实际的推演，其约束如下：
$$k_p=\left(\alpha +\beta \right)k_D{k}_l=\alpha \beta k_D{k}_D=?\Delta k_p\left(\bullet \right)=(\alpha +\beta )\Delta k_D\left(\bullet \right)\Delta k_l\left(\bullet \right)=\alpha \beta \Delta k_D\left(\bullet \right)\Delta k_D\left(\bullet \right)=\hat{a}{\phi }^2(\bullet )$$
  上面约束中的$alpha>0$和$\beta >0$和自适应的参数a的更新准则在后面会给出，$\phi$是与神经网络中的激活函数有关的函数量，且将这几个参数作为已知量看待，通过对于上面的约束的观察，发现其实只要确定了$k_D$，其他参数全部可以通过约束关系确定下来，所以，通过引入误差的滤波函数，控制器的建模参数其实简化了很多，控制系统变得更加的可靠。
对于一般化误差$E=2\gamma z+{\gamma }^2{\int }_0^{t}z\left(\bullet \right)d\tau +\frac{dz}{dt}$的可解释性问题，考虑设$y\left(t\right)={\int }_0^{t}zdt$，那么$E$可以转换为$E=\left(\alpha +\beta \right)\dot{y}+\alpha \beta y+\ddot{y}$，将$E$通过拉普拉斯变换，转换成$E\left(s\right)=\left(s+\alpha \right)\left(s+\beta \right)Y\left(s\right)$，便于进行因式分解，将本式进行等价转换，得到$Y\left(s\right)=\frac{1}{\left(s+\alpha \right)\left(s+\beta \right)}E\left(s\right)$，这在控制系统中属于非常稳定的滤波器，其有两个极点，位于实轴的两侧，一个$\alpha$一个$\beta$，这样得到极值保证了$E$最小，就可以保证$z$最小，从而保证了$e$（误差）最小。

3.5 对于方系统与非方系统的应用

  对于方系统的PID控制数学建模考虑加入可控的参数在神经网络中，根据上面章节的推论，可以得到方系统PID控制的数学模型：
$$u=\left(k_p+\Delta k_p\left(\bullet \right)\right)\Lambda z+\left(k_l+\Delta k_l\right)\Lambda {\int }_0^{t}z\left(\bullet \right)d\tau +\left(k_D+\Delta k_D\right)\Delta \frac{dz}{dt}$$
  可见此处模型只是将上节推论的公式的各项添加了一个参数矩阵$\Lambda$，在方系统中，$\Lambda$是一个单位矩阵，其约束与上节相同：
$$k_p=\left(\alpha +\beta \right)k_D{k}_l=\alpha \beta k_D{k}_D=?\Delta k_p\left(\bullet \right)=(\alpha +\beta )\Delta k_D\left(\bullet \right)\Delta k_l\left(\bullet \right)=\alpha \beta \Delta k_D\left(\bullet \right)\Delta k_D\left(\bullet \right)=\hat{a}{\phi }^2(\bullet )$$
  在对自适应参数$\hat{a}$在神经网络的更新策略中，遵循以下原则：
$$\dot{\hat{a}}=-{\sigma }_0\hat{a}+{\sigma }_1{\phi }^2(\bullet ){||E||}^2$$
  其中，${\sigma }_0$与${\sigma }_1$为正数参数。经过下列引理证明，其具有可行性。

  对于非方系统的PID控制器设计模型，由于其输入信号与输出信号不同，所以其矩阵并非方阵，非方系统的矩阵设为$B\left(\bullet \right)=B_0(\bullet )M(\bullet )$，其中$B_0(\bullet )\in R^{m\times l}$为行满秩的有界矩阵，$M(\bullet )\in R^{l\times l}$为严格正定或者负定的矩阵，关于非方系统的PID设计数学模型基本与方系统相同。
$$u=\left(k_p+\Delta k_p\left(\bullet \right)\right)\Lambda z+\left(k_l+\Delta k_l\right)\Lambda {\int }_0^{t}z\left(\bullet \right)d\tau +\left(k_D+\Delta k_D\right)\Delta \frac{dz}{dt}$$
  对于$\Lambda$，其与方系统中的单位阵不同，在非方系统的数学模型中，$\Lambda =\frac{B_0^T}{||B_0||}$，其余约束与方系统相同，分别为：
$$k_p=\left(\alpha +\beta \right)k_D{k}_l=\alpha \beta k_D{k}_D=?\Delta k_p\left(\bullet \right)=(\alpha +\beta )\Delta k_D\left(\bullet \right)\Delta k_l\left(\bullet \right)=\alpha \beta \Delta k_D\left(\bullet \right)\Delta k_D\left(\bullet \right)=\hat{a}{\phi }^2(\bullet )$$
  自适应参数的更新过程仍然遵循$\dot{\hat{a}}=-{\sigma }_0\hat{a}+{\sigma }_1{\phi }^2(\bullet ){||E||}^2$，经过以下图示引理可以证明其在MIMO系统中的可行性：

4. 总体设计

4.1 参数更新总体设计

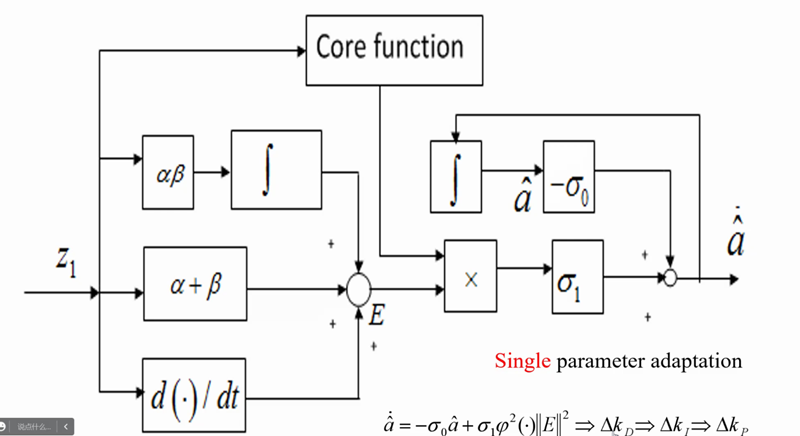
  神经网络自适应的PID控制器的参数更新设计框图如下图所示，将滤波后的误差$e$映射成为$z_1$，通过乘积形式的${\gamma }^2$参数$\alpha \beta$（$\alpha$与$\beta$为拉普拉斯变换再因式分解后的极点）和和形式的$\gamma$参数$\alpha +\beta$以及随时间变化的$d(\bullet )$，将PID的比例部分、积分部分、微分部分进行等价变换、因式分解和加权求和的形式得到一般化的误差$E$，将$E$与神经网络中的激活函数的运算乘参数${\sigma }_1$，将累积的旧的$\hat{a}$乘$-{\sigma }_0$，将两部分求和去更新自适应参数$\hat{a}$，最终的更新学习训练的过程并不是通过设置比例系数、积分系数、微分系数来逼近良好的结果，而是有单一的自适应参数$\hat{a}$。

4.2 系统总体设计

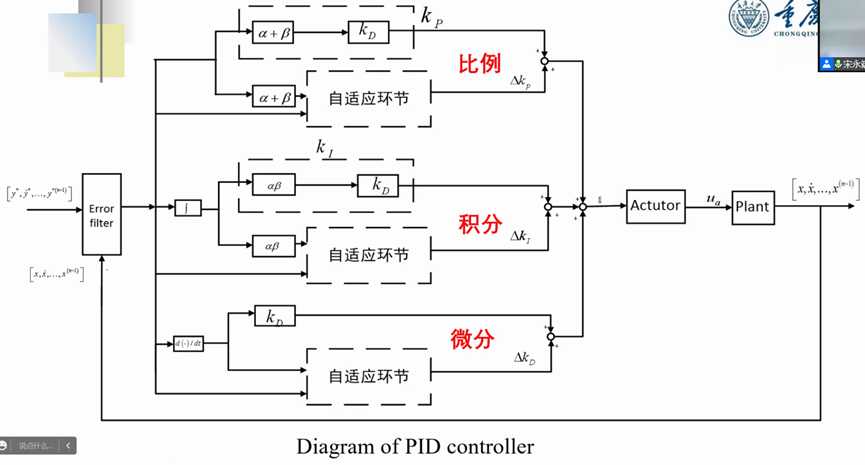
  从参数更新的角度去分析系统设计的框图，这一部分也是设计最核心、最重要的，本节是从总体设计的角度来分析总体设计的框图，总体设计框图如下图所示，系统输入通过误差滤波生成滤波后的误差，通过恒定的比例系数部分$k_p$和随时间变化的比例系数$\Delta k_p$进行加权求和，从而生成比例部分的设计，恒定比例系数部分$k_p$包括了$\alpha +\beta$决定的$k_D$，随时间变化部分的部分包含了$\alpha +\beta$决定的自适应的环节，细节已经在上面的系统设计中阐释，不再赘述；通过恒定的积分系数部分$k_l$和随时间变化的积分系数$\Delta k_l$进行加权求和，从而生成积分部分的设计，恒定积分系数部分$k_l$包括了$\alpha \beta$决定的$k_D$，随时间变化部分的部分包含了$\alpha \beta$决定的自适应的环节；通过恒定的微分系数部分$k_D$和随时间变化的比例系数$\Delta k_D$进行加权求和，从而生成微分部分的设计，恒定微分系数部分$k_D$，随时间变化部分的部分属于自适应的环节；综上三个部分的设计，将输出信号给予执行器，在实际的闭环系统工作中得到反馈信号，将反馈信号再次作为输入计算误差输入误差滤波器，反复迭代，直到结果收敛到满意的程度。

5. 应用与扩展

5.1 机器人机械臂方面的应用

  在机器人的关节空间当中，关节空间是典型的方系统，而末端执行结构（抓取结构）的任务空间是非方系统，其n关节严格物理连接的机器人操作器的数学建模如下图所示：

  在方系统的关节空间轨迹中，执行器的建模如下图所示：

  设定$y=x_1=q\in R^n,z=e_1=x_1-y^{\ast }=q-q^{\ast }$用于表征关节空间的角度误差，那么多关节机器人PID控制器的数学建模如下：
$$u=\left(k_p+\Delta k_p\left(\bullet \right)\right)\Lambda z+\left(k_l+\Delta k_l\right)\Lambda {\int }_0^{t}z\left(\bullet \right)d\tau +\left(k_D+\Delta k_D\right)\Delta \frac{dz}{dt}$$
  约束与第三章的设计中所述一致，由于关节空间中是方系统，所以$\Lambda$为单位阵，在自适应参数的更新原则$\dot{\hat{a}}=-{\sigma }_0\hat{a}+{\sigma }_1{\phi }^2(\bullet ){||E||}^2$ 中，${\phi }^2(\bullet )$是NN逼近或者说重构的核心函数。
  在任务空间的非方系统中，设定三维笛卡尔坐标系空间下的$X\in R^3$，动态映射$X^{\ast }=\epsilon (q)$，设定$y^{\ast }=X^{\ast }\in R^3,y=x_1=X,z=e=X-X^{\ast }$（也即末端操作空间的位置误差），误差滤波函数如下：
$$\ddot{z_1}=J\left(\bullet \right)\ddot{q}-\ddot{y^{\ast }}=B\left(\bullet \right)u+F(\bullet )$$
  其约束$J\left(\bullet \right)=\frac{\partial \epsilon (q)}{\partial q}\in R^{3\times n}$为雅可比矩阵，同时F与B满足下图的要求：

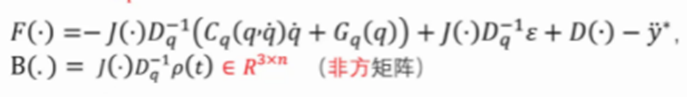
  多关节机器人任务空间PID控制器的数学建模如下：
$$u=\left(k_p+\Delta k_p\left(\bullet \right)\right)\Lambda z+\left(k_l+\Delta k_l\right)\Lambda {\int }_0^{t}z\left(\bullet \right)d\tau +\left(k_D+\delta k_D\right)\Delta \frac{dz}{dt}$$
  其约束不再赘述，其误差$z=e=X-X^{\ast }$（末端操作空间位置误差），由于是非方系统，那么$\Lambda =\frac{J^T}{||J||}$，在自适应参数的更新原则$\dot{\hat{a}}=-{\sigma }_0\hat{a}+{\sigma }_1{\phi }^2(\bullet ){||E||}^2$中，${\phi }^2(\bullet )$是NN逼近或者说重构的核心函数。

6. 总结

  神经网络自适应的PID具有极强的现实意义，因为PID作为影响力和应用面极大的经典控制算法，对于其优化能够带来工业界、控制工程领域的极大便利，在实际的应用场景中，对于PID的使用，往往通过手动调参的方式去实验，在一些损失影响不大的系统中，往往耗费时间，在损失影响较大的系统中，往往会造成一些不可估量的成本耗费，而引入神经网络自适应的PID能够完成无需人工试错的环节，节省大量的人力和资源成本；同时，经典控制理论与人工智能神经网络的结合，将会给控制工程带来很强扩展性，能够实现PID控制算法的参数关联自动调整-解析算法，通过自动编程的方式实现实时自适应调整；由于PID控制系统有了自适应的参数，其容错率将大大提高，鲁棒性也大大提高；通过学术前辈的工作，将神经网络自适应的PID的数学建模建立出来，优化参数量，通过神经网络的方式去逼近，易于实现且使得成本可控，当然在神经网络的调优上，仍然需要做一些工作，目前关于PID的学术论文在LTI系统和UNS系统两个领域里近年来出现了很多可行性高的新思维的碰撞，在可解释性、自适应性和容错性上也各不相同，足以证明PID在控制领域的重要地位，也足以证明PID和神经网络结合的必要性和可扩展性。