三维曲线的表示方式有几种方式：包括参数多项式曲线，艾特肯多项式算法，拉格朗日基多项式，埃尔米特形式曲线，贝塞尔曲线等。最后我们会讨论样条曲线的方式。

一：参数多项式曲线：

说道曲线，我们很自然的想到一种应用最广的曲线函数，就是圆的参数描述方式：

$x(t)=cos(2\pi t ); y(t)=sin(2\pi t)$

而多项式参数的表示形式是类似如下形式：

$p(t)=c_{0}+c_{1}t+c_{2}t^{2}+...+c_{n-1}t_{n-1}+c_{n}t_{n}$

其中n被称为多项式的次数。这也是一个单项式形式或叫幂形式。

二：艾特肯算法：

他是利用一种分而治之的方式实现的额曲线，也就是一条仅插入前n-1个点的曲线，忽略最后的点；另一条插入最后n-1个点的曲线，二不用担心第一个点。然后，将这两条曲线混合在一起即可。

艾特肯算法可以将二次曲线创建为两条线段的混合。

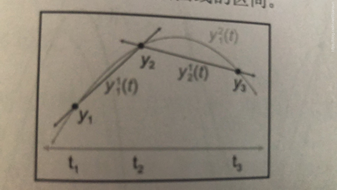
相应的两个控制点之间的额线性差值公式是：

$y_{1}^{1}(t)=\frac{(t_{2}-t)*y1+(t-t_{1})*y2)}{t_{2} - t_{1}}$ ,

$y_{2}^{1}(t)=\frac{(t_{3}-t)*y2+(t-t_{2})*y3)}{t_{3} - t_{2}}$

将连个线段再做一次差值运算得到二次曲线为：

$y_{1}^{2}(t)=\frac{(t_{3}-t)*[y_{1}^{1}(t)]+(t-t_{2}))*[y_{2}^{1}(t)]}{t_{3} - t_{1}}$

也就是根据你分的段先计算每段的结果，再结合每两端的结果，不断下去。相当于归并的思想。

艾特肯的算法是有限的，如下图左侧展示的是三条线段混合形成两个二次段。右图展示了两条二次曲线的混合产生了我们一直在寻找的最终结果：一个插值所有四个控制点的三次样条。

但是这个多项式插值病没有真正为我们提供集合设置中曲线设计所需的控制类型。

三：拉格朗日基多项式：

关于拉格朗日多项式的公式为：

$p(t)=\sum_{t=1}^{n}y_{i}\varrho _{i}(t)=y_{1}\varrho _{1}(t)+y_{2}\varrho _{2}(t)+...+y_{n-1}\varrho _{n-1}(t)+y_{n}\varrho _{n}(t)$

用于节点矢量t1，L，tn的拉格朗日基多项式看起来像：

$\varrho _{i}(t)=\prod_{1\leqslant j\leqslant n}\frac{t-t_{j}}{t_{i}-t{j}}=\frac{t-t_{0}}{t_{i}-t{0}}...\frac{t-t_{i-1}}{t_{i}-t{i-1}}\frac{t-t_{i+1}}{t_{i}-t{i+1}}\frac{t-t_{n}}{t_{i}-t{n}}$

如果我们带入均匀矢量（0,1/3,2/3,1）的话。相应对的值为：

具体计算为：

$\varrho _{1}(t)=\frac{(t - \frac{1}{3})*(t - \frac{2}{3})*(t - 1)}{(0-\frac{1}{3})*(0-\frac{2}{3})*(0-1)}$

$\varrho _{2}(t)=\frac{(t - 0)*(t - \frac{2}{3})*(t - 1)}{(\frac{1}{3}-0)*(\frac{1}{3}-\frac{2}{3})*(\frac{1}{3}-1)}$

$\varrho _{3}(t)=\frac{(t - 0)*(t - \frac{1}{3})*(t - 1)}{(\frac{2}{3}-0)*(\frac{2}{3}-\frac{1}{3})*(\frac{2}{3}-1)}$

$\varrho _{4}(t)=\frac{(t - 0)*(t - \frac{1}{3})*(t - \frac{2}{3})}{(1-0)*(1-\frac{1}{3})*(1-\frac{2}{3})}$

通过上式可以看出，拉格朗日基多项式是根据当前计算的i来确定其他项对自己的差值。比如 $\varrho _{1}(t)$ 就是把第一项0作为基础，跟其他项（除了自己）相减。分号上方是t跟除了0之外的相减，下方是0减去除了自己外的值。最终得到下式。

$\varrho _{1}(t)=-(9/2)t^{3}+9t^{2}-(11/2)t+1,$

$\varrho _{2}(t)=(27/2)t^{3}+(45/2)t^{2}-(9)t,$

$\varrho _{3}(t)=-(27/2)t^{3}+(18)t^{2}-(9/2)t,$

$\varrho _{4}(t)=(9/2)t^{3}-(9/2)t^{2}+t,$

所以p(t)为：

$p(t)=y_{1}\varrho _{1}(t)+y_{2}\varrho _{2}(t)+y_{3}\varrho _{3}(t)+y_{4}\varrho _{4}(t)$

下面展示了多项式分解的曲线：

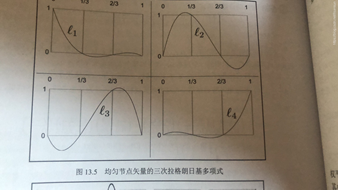
$p(t)=y_{1}\varrho _{1}(t)+y_{2}\varrho _{2}(t)+y_{3}\varrho _{3}(t)+y_{4}\varrho _{4}(t)$

总和得到一条我们最终的曲线

四：多项式插值的汇总

艾特肯的算法是一种基于重复线性插值的几何方法，通过它可以在不知道曲线的多项式的情况下计算给定t的曲线上的点。拉格朗日插值通过创建仅依赖于节点矢量的基函数来工作。但是多项式插值不理想在于不能控制越线（指超过了两个中间控制点的y值）的情况。

五：埃尔米特曲线：

它是通过端点处的切线控制曲线的形状，它通过列出起始位置和结束位置以及导数来制定曲线。三次曲线只有四个系数，这允许仅指定一阶导数，即端点处的速度。因此，描述埃尔米特形式的三次曲线可归结为以下4条信息：

t=0时的起始位置。

t=0时的一阶导数（初始速度）

t=1时的结束位置。

t=1时的一阶导数（最终速度）

y以下是一些三次埃尔米特曲线的例子：

假设三次多项式函数为P(t) = c0 + c1*x + c2*x² + c3*x³。

然后我们知道p(t)的导数是： ${P(t)}'=c1+2*c2x+3*c3x^{2}$ 。而导数就是他的速度

可得埃尔米特条件的方程组是：

p(0)=p0=>c0=p0 (这里是相当于把0带入P(t))

v(0)=v0=>c1=v0 (这里是相当于把0带入 ${P(t)}'$ )

v(1)=v1=>c1+2c2+3c3=v1 (这里是相当于把1带入 ${P(t)}'$ )

p(1)=p1=>c0+c1+c2+c3=p1 (这里是相当于把1带入P(t))

前后两个公式指定端点，中间两个指定速度。

然后求解上面的方程组，产生一种通过埃尔米特位置和导数来计算单项式系数的方法：

$c_{0}=p_{0}$

$c_{1}=v_{0}$

$c_{2}=-3p_{0}-2v_{0}-v_{1}+3p_{1}$

$c_{3}=2p_{0}+v_{0}+v_{1}-2p_{1}$

上面解出了四个未知项。

使用矩阵的方式表示为：

$p(t)=Ct=PHt=\begin{bmatrix} |& |& |& | \\ p_{0}& v_{0}& v_{1}& p_{1}\\ |& |& |& | \end{bmatrix}\begin{bmatrix} 1& 0& -3& 2\\ 0& 1& -2& 1\\ 0& 0& -1& 1\\ 0& 0& 3& -2 \end{bmatrix}\begin{bmatrix} 1\\ t\\ t^{2}\\ t^{3} \end{bmatrix}$

然后我们合并后两个矩阵得：

$p(t)=Ct=PHt=\begin{bmatrix} |& |& |& | \\ p_{0}& v_{0}& v_{1}& p_{1}\\ |& |& |& | \end{bmatrix}\begin{bmatrix} 1-3t^{2}+2t^{3}\\ t-2t^{2}+t^{3}\\ -t^{2}+t^{3}\\ 3t^{2}-2t^{3} \end{bmatrix}$

也就得到三次埃尔米特基函数：

$H_{0}(t)=1-3t^{2}+2t^{3}$

$H_{1}(t)=t-2t^{2}+t^{3}$

$H_{2}(t)=-t^{2}+t^{3}$

$H_{3}(t)=3t^{2}-2t^{3}$

这个是三次埃尔米特曲线的设计，当然也可以得到更高次数的埃尔米曲线设计。在使用三次样条的情况下，可以指定终点的位置（“0阶”导数）和速度（一阶导数）。当同时还指定了加速度（二阶导数）时，会出现5次埃尔米特曲线。

六：贝塞尔曲线：

贝塞尔曲线采用的是近似方法而不是插值：虽然他们确实通过了第一个和最后一个控制点，但他们只能通过内部点附近。所以贝塞尔控制点被称为“控制点”而不是“节点”。

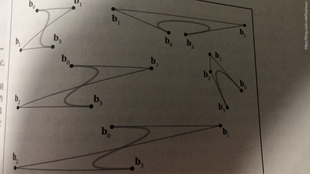
艾特肯的算法在贝塞尔曲线算法中的对应物是de Casteljau算法，他是一种通过重复线性插值构造贝塞尔曲线的递归几何级数。

6.1关于de Casteljau算法：

他可以通过原来的4个控制点 $b_{0}^{0},...,b_{3}^{0}$ 开始，可以推导出3个新点 $b_{0}^{1}$ ， $b_{1}^{1}$ 和 $b_{2}^{1}$ ，然后这三个点的每一对之间的另一轮插值将给出两个点 $b_{0}^{2}$ 和 $b_{1}^{2}$ ，最终的插值将产生点 $b_{0}^{3}=p(t)$ ，这个点就是我们想要的曲线的点。

得到de Casteljau的递归关系：

$b_{t}^{0}(t)=b_{i}$

$b_{i}^{n}(t)=(1-t)[b_{i}^{n-1}(t)]+t[b_{i+1}^{n-1}(t)]$

下面这张图展示了t在0.25,0.5,0.75时的点。

下面是de Casteljau算法中的三次曲线的层级关系

Vector3 deCasteljau(
    int n,                //曲线的阶，点的数量
    Vector3 points[],     //点的数组，将被覆盖
                          //因为该算法是在原地执行的
    float t               //要评估的参数值
){
    //原地执行转换
    while (n > 1)
    {
        --n;
        //执行下一轮的插值
        //曲线的次数减1
        for (int i = 0; i < n; ++i)
        {
            points[i]=points[i] * (1.0f - t) + points[i+1] * t;
        }
    }
    //最后剩下的一个就是结果
    return points[0];
    
}

线性情况直接来自递归关系，无需任何实际操作，具体如下：

$b_{i}^{1}(t)=(1-t)[b_{i}^{0}(t)]+t[b_{i+1}^{0}(t)]=b_{i}+t(b_{i+1}-b_{i})$

二次多项式为：

$b_{i}^{2}(t)=(1-t)[b_{i}^{1}(t)]+t[b_{i+1}^{1}(t)]=b_{i}+t(2b_{i+1}-2b_{i})+t^{2}(b_{i}-2b_{i+1}+b_{i+2})$

使用矩阵表示法的二次贝塞尔曲线

$p(t)=Ct=BMt=\begin{bmatrix} |& |& | \\ b_{0}& b_{1}& b_{2}\\ |& |& |\end{bmatrix}\begin{bmatrix} 1& -2& 1\\ 0& 2& -2\\ 0& 0& 1\end{bmatrix}\begin{bmatrix} 1\\ t\\ t^{2} \end{bmatrix}$

单项式形式的三次贝塞尔曲线：

$p(t)=b_{0}^{3}(t)=b_{i}+t(3b_{i+1}-3b_{i})+t^{2}(3b_{i}-6b_{i+1}+3b_{i+2})+t^{3}(-b_{i}+3b_{i+1}-3b_{i+2}+b_{i+3})$

通过单项式的三次贝塞尔曲线可以得到：

$c_{0}=b_{0}$

$c_{1}=-3b_{0}+3b_{1}$

$c_{2}=3b_{0}-6b_{1}+3b_{2}$

$c_{3}=-b_{0}+3b_{1}-3b_{2}+b_{3}$

单项式形式的三次贝塞尔曲线矩阵：

$p(t)=Ct=BMt=\begin{bmatrix} |& |& |& | \\ b_{0}& b_{1}& b_{2}& b_{3}\\ |& |& |& | \end{bmatrix}\begin{bmatrix} 1& -3& 3& -1\\ 0& 3& 6& 3\\ 0& 0& 3& -3\\ 0& 0& 0& 1 \end{bmatrix}\begin{bmatrix} 1\\ t\\ t^{2}\\ t^{3} \end{bmatrix}$

6.2：伯恩斯坦基多项式

de Casteljau是基于系数t的幂实现的多项式，我们还可以通过收集控制点上的项而不是t的幂来写出贝塞尔形式的多项式。

一次多项式：

$b_{i}^{1}(t)=(1-t)[b_{i}^{0}(t)]+t[b_{i+1}^{0}(t)]=(1-t)b_{i}+tb_{i+1}$

二次多项式：

$b_{i}^{2}(t)=(1-t)[b_{i}^{1}(t)]+t[b_{i+1}^{1}(t)]=(1-t)[(1-t)b_{i}+tb_{i+1}]+t[(1-t)b_{i+1}+tb_{i+2}]=(1-t)^{2}b_{i}+2t(1-t)b_{i+2}+t^{2}b_{i+2}$

三次多项式：

$b_{i}^{3}(t)=(1-t)[b_{i}^{2}(t)]+t[b_{i+1}^{2}(t)]=(1-t)[(1-t)^{2}b_{i}+2t(1-t)b_{i+1}+t^{2}b_{i+2}]+t[(1-t)^{2}b_{i+1}+2t(1-t)b_{i+2}+t^{2}b_{i+3}]=(1-t)^{3}b_{i}+3t(1-t)^{2}b_{i+1}+3t^{2}(1-t)b_{i+2}+t^{3}b_{i+3}$