分治算法基本概念
在计算机科学中,分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小,越容易直接求解,解题所需的计算时间也越少。例如,对于n个元素的排序问题,当n=1时,不需任何计算。n=2时,只要作一次比较即可排好序。n=3时只要作3次比较即可,…。而当n较大时,问题就不那么容易处理了。要想直接解决一个规模较大的问题,有时是相当困难的。
分治算法应用情况:
1) 问题的规模越小越容易解决
2) 问题可以分解为若干个规模较小的相同问题
3) 子问题的解可以合并为该问题的解;
4) 各个子问题是相互独立的
下面给一个例子,棋盘覆盖问题:
问题描述:在一个2^k×2^k (k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为特殊方格。显然,特殊方格在棋盘中可能出现的位置有4^k种,因而有4^k种不同的棋盘。棋盘覆盖问题(chess cover problem)要求用如图所示的4种不同形状的L型骨牌覆盖给定棋盘(4×4棋盘)上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
解决思路:
k>0时,可将2^k×2^k的棋盘划分为4个2^(k-1)×2^(k-1)的子棋盘。这样划分后,由于原棋盘只有一个特殊方格,所以,这4个子棋盘中只有一个子棋盘包含该特殊方格,其余3个子棋盘中没有特殊方格。为了将这3个没有特殊方格的子棋盘转化为特殊棋盘,以便采用递归方法求解,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种划分策略,直至将棋盘分割为1×1的子棋盘。
具体步骤:
1、我们首先吧整个棋盘划分为左上、右上、左下、右下四块,然后判断特殊的方块在哪一块里面。
2、假如在左上这一块区域里面,我们就再把这块区域划分四块,直到找到为止。
3、其他没有特殊方块的区域,我们需要开始填充L形的牌。
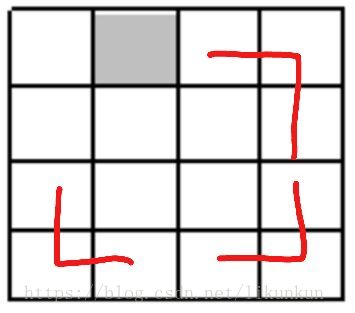
4、我们采取,先把最周围的填上L形牌。如下图所示:
5、我们发现,分割成4块之后,没有特殊方块的那3块区域只要如上图填充完后,中间正好剩下一块L形区域,所以我们设置每块区域里的靠近中间的方块 为 当前子矩阵里的 特殊方块,这样做的目的是,让每次分割正好会多出3块其他的就也正好可以放下L形区域。
6、对于之前存在特殊方块的区域,我们通过直接递归进行下一次分割(如图为左上)区域,就会吧接下来的填充完成。
具体的实现请看代码(java实现):
public class ChessProblem {
int size;//容量
int[][] board;//棋盘
int specialROW;//特殊点横坐标
int specialCOL;//特殊点纵坐标
int number = 0;//L形编号
public ChessProblem(int specialRow, int specialCol, int size) {
this.size = size;
this.specialCOL = specialCOL;
this.specialROW = specialROW;
board = new int[size][size];
}
//specialROW 特殊点的行下标
//specialCOL 特殊点的列下标
//leftRow 矩阵的左边起点行下标
//leftCol 矩阵左边起点的列下标
//size 矩阵的宽或者高
public void setBoard(int specialROW, int specialCOL, int leftROW, int leftCOL, int size) {
if (1 == size) {
return;
}
int subSize = size / 2;
number++;
int n = number;//注意这里一定要吧number存在当前的递归层次里,否则进入下一层递归全局变量会发生改变
//假设特殊点在左上角区域
if (specialROW < leftROW + subSize && specialCOL < leftCOL + subSize) {
setBoard(specialROW, specialCOL, leftROW, leftCOL, subSize);
}
else {
//不在左上角,设左上角矩阵的右下角就是特殊点(和别的一起放置L形)
board[leftROW + subSize - 1][leftCOL + subSize - 1] = n;
setBoard(leftROW + subSize - 1, leftCOL + subSize - 1, leftROW, leftCOL, subSize);
}
//假设特殊点在右上方
if (specialROW < leftROW + subSize && specialCOL >= leftCOL + subSize) {
setBoard(specialROW, specialCOL, leftROW, leftCOL + subSize, subSize);
}
else {
//不在右上方,设右上方矩阵的左下角就是特殊点(和别的一起放置L形)
board[leftROW + subSize -1][leftCOL + subSize] = n;
setBoard(leftROW + subSize -1, leftCOL + subSize, leftROW, leftCOL + subSize, subSize);
}
//特殊点在左下方
if (specialROW >= leftROW + subSize && specialCOL < leftCOL + subSize) {
setBoard(specialROW, specialCOL, leftROW + subSize, leftCOL, subSize);
}
else {
//不在左下方,设左下方矩阵的右上角就是特殊点(和别的一起放置L形)
board[leftROW + subSize][leftCOL + subSize - 1] = n;
setBoard(leftROW + subSize, leftCOL + subSize - 1, leftROW + subSize, leftCOL, subSize);
}
//特殊点在右下角
if (specialROW >= leftROW + subSize && specialCOL >= leftCOL + subSize) {
setBoard(specialROW, specialCOL, leftROW + subSize, leftCOL + subSize, subSize);
}
else {
//不在右下角,设右下角矩阵的左上就是特殊点(和别的一起放置L形)
board[leftROW + subSize][leftCOL + subSize] = n;
setBoard(leftROW + subSize, leftCOL + subSize, leftROW + subSize, leftCOL + subSize, subSize);
}
}
public void printBoard(int specialRow,int specialCol,int size) {
setBoard(specialRow, specialCol, 0, 0, size);
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board.length; j++) {
System.out.print(board[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int N = 4;
int specialRow = 0;
int specialCol = 1;
ChessProblem chessProblem = new ChessProblem(specialRow , specialCol , N);
chessProblem.printBoard(specialRow, specialCol, N);
}
}
这只是分治算法中的一个比较典型的问题,包括二分法查找、合并排序,快速排序等,都是运用了分治法的思想。
这次主要是通过棋盘覆盖问题看分治法的内容。