机器学习笔记 - 特殊类型的矩阵和向量

1、对角矩阵

对角矩阵，除了对角线之外全都是0。

（1）例1：方阵对角矩阵

（2）例2：非方阵对角矩阵

（3）例3：对角矩阵表示为diag(v)

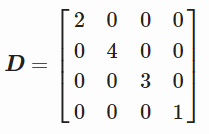
可以使用如下表示

python代码参考

v = np.array([2, 4, 3, 1])
print(np.diag(v))

输出如下

[[2 0 0 0]
 [0 4 0 0]
 [0 0 3 0]
 [0 0 0 1]]

（4）对角矩阵和向量相乘

有如下矩阵D和向量x

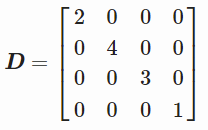
矩阵和向量相乘只是将向量的每个元素乘以 v(上一个例子的向量v)

（5）非方阵具有相同的性质

有如下矩阵D和向量x

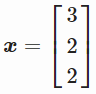
则矩阵D和向量x相乘如下

（6）方阵对角矩阵存在逆矩阵

如果对角线的所有条目都非零，则存在方对角矩阵的逆矩阵。如果是这种情况，倒数很容易找到。此外，如果矩阵是非正方形的，则不存在逆矩阵。

python代码参考

A = np.array([[2, 0, 0, 0], [0, 4, 0, 0], [0, 0, 3, 0], [0, 0, 0, 1]])
A_inv = np.array([[1/2., 0, 0, 0], [0, 1/4., 0, 0], [0, 0, 1/3., 0], [0, 0, 0, 1/1.]])
print(A.dot(A_inv))

输出了单位矩阵

[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]

2、对称矩阵

如果矩阵是对称的，则有矩阵等于它的转置矩阵，前提是需要是方阵。

设有如下矩阵

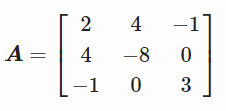
python参考代码，求矩阵的转置

A = np.array([[2, 4, -1], [4, -8, 0], [-1, 0, 3]])
print(A.T)

输出如下，等于原矩阵

[[ 2  4 -1]
 [ 4 -8  0]
 [-1  0  3]]

3、单位向量

单位向量是长度（范数）等于 1 的向量。它可以用带帽子的字母表示：。在很多地方也可以称之为归一化。

归一化向量的方法有很多……机器学习中的一个常见预处理步骤是在将向量传递给某些机器学习算法之前对向量进行归一化，例如，在训练支持向量机 (SVM) 之前。

对向量进行归一化的一种方法是缩放向量以使其长度为 1，即单位范数。有不同的方法来定义“长度”，例如 L1 或 L2 归一化。如果你使用 L2 归一化，“单位范数”本质上意味着如果我们对向量中的每个元素进行平方，并将它们相加，它将等于1。

（请注意，这种归一化通常也称为、单位范数或向量长度等于1、单位向量）不要被绕晕。

（1）例1：将向量 L2 归一化为单位向量

import numpy as np
from sklearn import preprocessing
 
# 2 samples, with 3 dimensions.
# The 2 rows indicate 2 samples.
# The 3 columns indicate 3 features for each sample.
X = np.asarray([[-1,0,1],
                [0,1,2]], dtype=np.float) # Float is needed.
 
# Before-normalization.
print(X)
# Output,
# [[-1.  0.  1.]
#  [ 0.  1.  2.]]
 
# l2-normalize the samples (rows). 
X_normalized = preprocessing.normalize(X, norm='l2')
 
# After normalization.
print(X_normalized)
# Output,
# [[-0.70710678  0.          0.70710678]
#  [ 0.          0.4472136   0.89442719]]

检查得到的向量的范数是否为1

# Square all the elements/features.
X_squared = X_normalized ** 2
print(X_squared)
# Output,
# [[ 0.5  0.   0.5]
#  [ 0.   0.2  0.8]]
 
# Sum over the rows.
X_sum_squared = np.sum(X_squared, axis=1)
print(X_sum_squared)
# Output,
# [ 1.  1.]

（2）例2：将向量 L1 归一化为单位向量

X_normalized_l1 = preprocessing.normalize(X, norm='l1')
print(X_normalized_l1)
# [[-0.5   0.   0.5]
#  [  0.   0.3  0.67]]

检查得到的向量的范数是否为1

# Absolute value of all elements/features.
X_abs = np.abs(X_normalized_l1)
print(X_abs)
# [[0.5   0.   0.5]
#  [0     0.3  0.67]]
 
# Sum over the rows.
X_sum_abs = np.sum(X_abs, axis=1)
print(X_sum_abs)
# Output,
# [ 1.  1.]

（3）例3：手动计算单位向量

给定向量，v =(1,5,-2)

计算L2范数

则单位向量为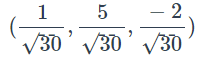，范数 = 1，即单位范数

4、正交向量

两个正交向量相隔 90° 角。两个正交向量的点积为 0。

让我们查看如下两个向量的可视化。

python代码

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

x = [0,0,2,2]
y = [0,0,2,-2]

plt.quiver([x[0], y[0]],
           [x[1], y[1]],
           [x[2], y[2]],
           [x[3], y[3]],
           angles='xy', scale_units='xy', scale=1)

plt.xlim(-2, 4)
plt.ylim(-3, 3)
plt.axvline(x=0, color='grey')
plt.axhline(y=0, color='grey')

plt.text(1, 1.5, r'$\vec{u}$', size=18)
plt.text(1.5, -1, r'$\vec{v}$', size=18)

plt.show()
plt.close()

可视化效果

矩阵和矩阵为正交矩阵。

它们的点积为0。

python代码参考

x = np.array([2, 2])
y = np.array([2, -2])
print(x.dot(y))

打印结果为

4、正交矩阵

（1）定义

正交矩阵很重要，如果列是相互正交的并且具有单位范数；并且行是相互正交的并且具有单位范数，则矩阵是正交的。

上面那一大段绕口的意思是有如下一个矩阵

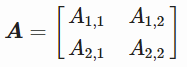
其中是正交向量。

并且也是正交向量。

那么矩阵就叫正交矩阵。

（2）性质1

正交矩阵具有以下性质：

假设有矩阵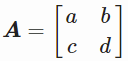并且有转置矩阵

则计算

我们可以看到向量[a c]的平方L2范数为，另因为A是正交的，所以行向量的范数为1，即单位范数。则有

即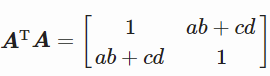

然后因为，并且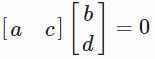

即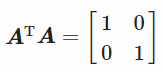

（3）性质2

如果则

证明如下

如果将等式两边都乘以则有

即

又因为

则即

（4）示例

使用正弦函数和余弦函数便于创建正交矩阵，我们有如下一个矩阵

使用如下代码依次测试行列是否正交、性质1、性质2。

A = np.array([[np.cos(50), -np.sin(50)], [np.sin(50), np.cos(50)]])

col0 = A[:, 0].reshape(A[:, 0].shape[0], 1)
col1 = A[:, 1].reshape(A[:, 1].shape[0], 1)
row0 = A[0, :].reshape(A[0, :].shape[0], 1)
row1 = A[1, :].reshape(A[1, :].shape[0], 1)

# 让我们检查行和列是否正交
print(col0.T.dot(col1))

print(row0.T.dot(row1))

# ATA=AAT=I
print(A.T.dot(A))

# 查看AT是否等于A-1
print(A.T)

print(numpy.linalg.inv(A))