机器学习笔记：支持向量机

— 抓住主线，全神贯注，决胜于速

1.SVM意义

支持向量机是一种二分类模型，基本模型是定义在特征空间的间隔最大的线性分类器。

间隔最大使它不同于感知机，感知机利用误分类最小的策略，得到分离超平面有无数个，而SVM加上间隔最大后，只有一个；

包括核技巧将其扩展为非线性分类器；

学习策略是间隔最大化，其可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。

支持向量机的学习算法就是求解凸二次规划的最优算法。

模型包含：线性可分支持向量机（硬间隔支持向量机），软间隔支持向量机，非线性支持向量机。

2.SVM模型

2.1 线性可分支持向量机

从二分类问题开始，给定一个特征空间上的训练数据集 $T=\{(x_1,y_1),\dots,(x_N,y_N)\}$ ，其中 $，x_i\in R^N，y_i\in\{+1,-1\}$ ，对于 $y$ 取值的限制是一个 trick，用函数间隔正负来判别分类正确性。一个重要的假设是，数据集线性可分。

学习的目标是找到的特征空间的分离超平面，用 $w\cdot x+b=0$ 表示，参数是法向量 $w$ 和截距 $b$ ，空间被划分为两个部分，正类和负类，法向量指向的一侧是正类。

使用公式
$d=\frac{w\cdot x+b}{|w|}$
求解点到面的距离是，法向量和 $x$ 内积运算有个夹角，这个夹角决定了距离的正负，而我们定义距离为正的是正样本，因而，可以说法向量指向的一侧是正类。

这里的 $w\cdot x$ 代表的是点积运算，就是 $w^T x$ 。

样本点到分离超平面的间隔分为函数间隔和几何间隔，SVM分类时， $w\cdot x+b$ 为正时，代表是正类，为负时，代表是负类。乘以标签值 $y$ 之后， $y(w\cdot x+b)$ 用来表示分类的正确与否，为正则代表分类正确，为负代表分类错误。 $|w\cdot x+b|$ 的值大小代表分类的置信度。

函数间隔： $\tilde{\gamma}=y_i(w\cdot x+b)$ ，进一步，定义超平面关于训练集T的函数间隔为所有点函数间隔的最小值，即 $\tilde{\gamma}=\min \tilde{\gamma}_i$ 。

几何间隔：很明显，当成比例的改变w和b时，函数间隔可以任意大小，所以定义几何间隔，表示空间中点到超平面的真实距离。即 $\tilde{\gamma}=\frac{y_i(w\cdot x+b)}{|w|}$ ，SVM学习的目标就是正确划分训练数据集并且几何间隔最大化的。

考虑如何求一个几何间隔最大的分离超平面，问题可以表述为约束最优化问题：
$\max\limits_{w,b} \quad \gamma \\ s.t.\quad y_i(\frac{w}{||w||}\cdot x_i+\frac{b}{||w||})\geq\gamma,\ i=1,\ldots N.$
可以改写为
$\max\limits_{w,b} \quad \frac{\tilde{\gamma}}{||w||} \\ s.t.\quad y_i(w\cdot x_i+b)\geq \tilde{\gamma},\ i=1,\ldots N.$
函数间隔 $\tilde{\gamma}$ 并不会影响问题的解，我们可以将 $w,b$ 重写为变量 $w/\tilde{\gamma},b/\tilde{\gamma}$ ，可以看出问题没有发生变化，而函数间隔变量没有了。因此，我们不妨直接令 $\tilde{\gamma}=1$ 。

这时，几何间隔变为 $\frac{1}{||w||}$ ，结合之前所述，函数间隔为1的点称为支持向量，而这些点的几何间隔则和 $w$ 有关系，需要具体的求解。

这时优化问题转化为
$KaTeX parse error: Expected 'EOF', got '\label' at position 99: …\ i=1,\ldots N.\̲l̲a̲b̲e̲l̲{raw}$
这是一个典型的凸二次规划问题。

可以求得最优解为 $w^*,b^*$ ，得到分离超平面： $w^*\cdot x+b^*=0$ ，分类决策函数为 $f(x)=sign(w^*\cdot x+b^*)$ 。

支持向量就是指的那些使约束条件成立的点，函数间隔为1.

我们使用对偶算法来对上述凸二次规划问题求解，首先写出拉格朗日函数，引入拉格朗日乘子 $\alpha_i\geq0,i=1,\dots,N$
$L(w,b,\alpha)=\frac{1}{2}||w||^2-\sum\limits_{i=1}^N\alpha_iy_i(w\cdot x_i+b)+\sum\limits_{i=1}^N \alpha_i$

求解 $\min\limits_{w,b}L(w,b,\alpha)$ ，使用偏导数为0
$\nabla_w L(w,b,\alpha)=w-\sum\limits_{i=1}^N\alpha_iy_ix_i=0\\ \nabla_b L(w,b,\alpha)=\sum\limits_{i=1}^N\alpha_iy_i=0$
得到
$w=\sum\limits_{i=1}^N\alpha_iy_ix_i\\ \sum\limits_{i=1}^N\alpha_iy_i=0$
代入可得
$L(w,b,\alpha)=\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jx_i\cdot x_j -\sum\limits_{i=1}^N\alpha_iy_i((\sum\limits_{j=1}^N\alpha_jy_jx_j)\cdot x_i+b)\\ +\sum\limits_{i=1}^N\alpha_i =-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jx_i\cdot x_j+\sum\limits_{i=1}^N\alpha_i$

求解时候注意， $\alpha_i$ 和 $y$ 是值，只有 $x_i$ 是向量，值是可以随意调换位置的，另外，求和符号相乘的处理规则要记住，很简单。

2.对偶问题为
$\min\limits_{\alpha} \quad \frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jx_i\cdot x_j-\sum\limits_{i=1}^N\alpha_i\\ s.t. \quad \sum\limits_{i=1}^N\alpha_iy_i=0 \\ \alpha_i\geq0$
解出 $\alpha_i^*$ 之后，求出w和b即可得到模型，其中可以得到至少有一个 $\alpha_j>0$ ，
$w^*=\sum\limits_{i=1}^N\alpha_i^*y_ix_i\\ b^*=y_j-\sum\limits_{i=1}^N\alpha_i^*y_ix_i\cdot x_j\\f(x)=w^*\cdot x+b^*\\$
可以看出，分类决策函数只依赖与输入 $x$ 和训练样本的内积。

从对偶问题解出的 $\alpha_i$ 对应着每一个训练样本，注意到式 $KaTeX parse error: Expected 'EOF', got '\ref' at position 1: \̲r̲e̲f̲{raw}$ 中有不等式约束，因此上述过程要满足KKT条件，即要求：
$\begin{cases} \alpha_i\geq0;\\y_if(x_i)-1\geq0;\\ \alpha_i(y_if(x_i)-1)=0. \end{cases}$
可以看出，对任意的训练样本 $(x_i,y_i)$ ，总有 $\alpha_i=0$ 或 $y_if(x_i)-1=0$ ，若前者，则该样本不会出现在 $w^*$ 的解中，若是后者，则必有 $，\alpha>0，y_if(x_i)=1$ ，所对应的样本点位于最大间隔边界上，是一个支持向量。这显示处支持向量一个重要的性质：训练完成后，大部分的训练样本都不会出现在判别函数中，最终模型只与支持向量有关。

2.2 软间隔最大化

当训练数据线性不可分时，不是所有的数据都能够划分正确，我们修改硬间隔最大化，使其成为软间隔最大化。通常情况下，训练数据线性不可分，我们把那些不可分的特异点去掉，剩下的样本点组成的集合是线性可分的。

线性不可分这里意味着，某些样本点不能满足函数间隔大于等于 1的约束条件，为了解决这个问题，对每个样本点引入一个松弛变量 $\xi_i\geq0$ 。使函数间隔加上松弛变量后大于等于1，这样约束条件变为
$y_i(w\cdot x_i+b)\geq 1-\xi_i$
相应的，每个松弛变量要在目标函数中加上“代价”，目标函数变为
$\frac{1}{2}||w||^2+C\sum\limits_{i=1}^N\xi_i$

这里的C称为惩罚参数，最小目标函数包含两层含义：使几何间隔尽可能小，同时使误分类点的个数尽可能小，C是调和二者的系数。

软间隔支持向量机的学习问题变为
$\min\limits_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum\limits_{i=1}^N\xi_i\\ s.t.\quad y_i(w\cdot x_i+b)\geq 1-\xi_i,\quad\ i=1,\ldots N\\ \xi_i\geq0,\quad\ i=1,\ldots N.$
该问题仍是一个凸二次规划问题，因为 $(w,b,\xi)$ 的解是存在的，可以证明 $w$ 的解是唯一的，但是 $b$ 的解不唯一，存在于一个区间内。

原始问题的对偶问题为
$\min\limits_{\alpha} \quad \frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jx_i\cdot x_j-\sum\limits_{i=1}^N\alpha_i\\ s.t. \quad \sum\limits_{i=1}^N\alpha_iy_i=0 \\ 0\leq\alpha_i\leq C$

求解对偶问题时，由于原问题由两项约束条件，因此有两组拉格朗日乘子（两组，不是两个），分别是 $，\alpha_i,\ \mu_i，i=1,\ldots N$ ，求解过程中得到约束条件 $C=\alpha_i+\mu_i,\mu_i\geq0$ ，这里把 $\mu_i$ 消去了，变为 $\alpha_i\leq C$ 。

前面说了，支持向量到超平面的函数距离为1，几何距离为 $\frac{1}{||w||}$ ，软间隔加入松弛变量后，由于 $y_i(w\cdot x_i+b)+\xi_i= 1$ ，可以看出样本点到支持向量的边界的几何距离就是 $\frac{\xi_i}{||w||}$ 。

类似的，上述过程要求满足KKT条件
$\begin{cases}\alpha_i\geq0,\quad \mu_i\geq0;\\y_if(x_i)+\xi_i-1\geq0;\\ \alpha_i(y_if(x_i)+\xi_i-1)=0.\\ \xi_i\geq0,\quad \mu_i\xi_i=0\end{cases}$
可以看出，对任意的训练样本 $(x_i,y_i)$ ，总有 $\alpha_i=0$ 或 $y_if(x_i)=1-\xi_i$ 。若前者，则该样本不会出现在 $w^*$ 的解中，若是后者，则必有 $，\alpha_i>0，y_if(x_i)=1-\xi_i$ ，是一个支持向量（不一定在最大间隔上）。若 $\alpha_i<C$ ，由于 $C=\alpha_i+\mu_i$ ，则 $\mu_i>0$ ，进而 $\xi_i=0$ ，该样本落在最大间隔边界上。否则，当 $\alpha_i=C$ ，有 $\mu_i=0$ ，此时若 $\xi_i\leq1$ ，则该样本落在分离超平面和最大间隔之间，若 $\xi_i>1$ ，则 $y_if(x_i)=1-\xi_i<0$ ，该样本点被分类错误。

2.3 合页损失函数

线性支持向量机学习，其模型为分离超平面和决策函数，学习策略是软间隔最大化，学习算法是凸二次规划。其还有另外一种解释，就是最小化目标函数
$\sum\limits_{i=1}^N[1-y_i(w\cdot x_i+b)]_++\lambda||w||^2$

合页损失函数为:
$[z]_+=\begin{cases}z, &z>0\\0, &z\leq0\end{cases}$

目标第一项表示，当样本点的函数间隔大于1时，损失为0，这是符合前面的思想的，否则损失就是 $1-y_i(w\cdot x_i+b)$ 。目标函数第二项是正则化项。

可以证明，软间隔线性支持向量机学习问题：
$\min\limits_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum\limits_{i=1}^N\xi_i\\s.t.\quad y_i(w\cdot x_i+b)\geq 1-\xi_i,\quad\ i=1,\ldots N\\\xi_i\geq0,\quad\ i=1,\ldots N.$
等价于最优化问题：
$\min_{w,b}\quad \sum\limits_{i=1}^N[1-y_i(w\cdot x_i+b)]_++\lambda||w||^2$

软间隔支持向量机原本的思想是，不满足最小间隔约束的点尽可能少，目标函数应该是
$\min\limits_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum\limits_{i=1}^N l_{0/1}(y_i(w\cdot x_i+b)-1)$
其中， $l_{0/1}$ 是0/1损失函数，
$l_{0/1}(z)=\begin{cases}1, &z>0\\0, &z\leq0\end{cases}$
但是，该损失函数非凸函数，不连续，不易求解，所以，通常用一些函数替代，比如

合页损失： $l_{hinge}(z)=\max(0,1-z)$
指数损失： $l_{exp}(z)=\exp(-z)$
对率损失： $l_{log}=\log(1+\exp(-z))$

è¿™é‡Œå†™å›¾ç‰‡æè¿°

2.4 支持向量回归(SVR)

è¿™é‡Œå†™å›¾ç‰‡æè¿°

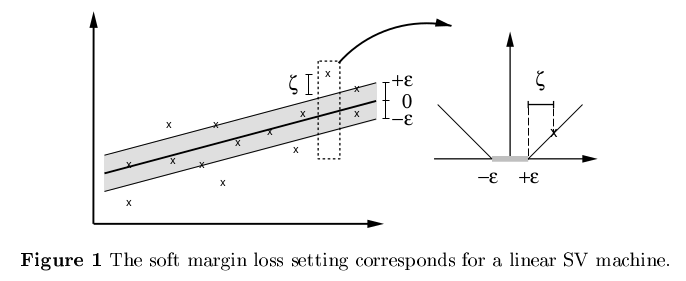
传统的回归模型基于模型输出和真实输出之间的差别来计算损失，当且仅当 $f(x)=y$ 时，损失才为0，支持向量回归模型中，假设我们能够容忍的偏差为 $\epsilon$ ，即当 $|f(x)-y|>\epsilon$ 时才计算损失，这相当于以 $f(x)$ 为中心，构建了一个宽度为 $2\epsilon$ 的间隔带，若训练样本落入此间隔带内，则被认为是预测正确的，不包含在损失计算中。

支持向量回归的目标函数为
$\min\limits_{\alpha} \quad \frac{1}{2}||w||^2+C\sum\limits_{i=1}^Nl_{\epsilon}(w\cdot x_i+b-y_i)$
其中，C为正则化常数， $l_{\epsilon}$ 是形如上面右图的损失函数
$l_{\epsilon}(z)=\begin{cases}0,& if|z|\le \epsilon\\ |z|-\epsilon,& otherwise.\end{cases}$

这里没有什么函数间隔与几何间隔，只有预测偏差 $f(x)-z$ 。

引入松弛变量 $\xi_i,\tilde{\xi_i}$ ，将优化问题重写为
$\min\limits_{w,b,\xi,\tilde{\xi_i}}\quad \frac{1}{2}||w||^2+C\sum\limits_{i=1}^N(\xi+\tilde{\xi_i})\\ s.t.\quad w\cdot x_i+b-y_i\leq \epsilon+\xi_i\\ \quad y_i-(w\cdot x_i+b)\leq \epsilon+\tilde{\xi_i}\\ \quad \xi_i\geq 0,\ \tilde{\xi_i}\geq0,\ i=1,\ldots N$
求解对偶问题，首先引入拉格朗日乘子 $\mu_i\geq0,\tilde{\mu_i}\geq0,\alpha_i\geq0,\tilde{\alpha}_i\ge0$ ，令拉格朗日函数对于变量的偏导数为零可以求得
$w=\sum\limits_{i=1}^N(\tilde{\alpha_i}-\alpha_i)x_i\\ \sum\limits_{i=1}^N(\tilde{\alpha_i}-\alpha_i)=0\\ \alpha_i+\mu_i=C\\ \tilde{\alpha_i}+\tilde{\mu_i}=C$
代入之后可以求得对偶问题为
$\max\limits_{\alpha,\tilde{\alpha_i}} \quad -\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N(\tilde{\alpha_i}-\alpha_i)(\tilde{\alpha_j}-\alpha_j)\alpha_jx_i\cdot x_j+\sum\limits_{i=1}^Ny_i(\tilde{\alpha_i}-\alpha_i)-\epsilon(\tilde{\alpha_i}-\alpha_i)\\ s.t. \quad \sum\limits_{i=1}^N (\tilde{\alpha_i}-\alpha_i)=0\\ \quad 0\leq\alpha,\tilde{\alpha_i}\leq C$
上述求解要满足KKT条件要求，
$\begin{cases} \alpha_i(f(x_i)-y_i-\epsilon-\xi_i)=0\\ \tilde{\alpha}_i(y_i-f(x_i)-\epsilon-\tilde{\xi_i})=0\\ \tilde{\alpha_i}\alpha_i=0,\ \tilde{\xi_i}\xi_i=0\\ (C-\alpha_i)\xi_i=0,\ (C-\tilde{\alpha_i})\tilde{\xi_i}=0 \end{cases}$
由原问题约束条件可以看出，当 $f(x_i)-y_i-\epsilon-\xi_i=0$ 时，由于 $\xi_i\geq0$ ，此时必定有 $f(x_i)-y_i-\epsilon\geq 0$ ，表明此时样本点一定落在了误差容许间隔外，而KKT第一个约束表明$f(x_i)-y_i-\epsilon-\xi_i=0 $或$ \alpha_i $必有一个成立，因而得出，只有当样本点在误差容许间隔外，即$ f(x_i)-y_i-\epsilon-\xi_i=0 $时，才可能有$ \alpha_i $取非零值。又因为$ f(x_i)-y_i-\epsilon-\xi_i=0 $和$ y_i-f(x_i)-\epsilon-\tilde{\xi_i}=0 $不可能同时成立（正负问题），所以$ \alpha_i $和$ \tilde{\alpha_i}$必有一个为0。

若是落在误差间隔内，由于 $|f(x_i)-y_i|<\epsilon$ ，且 $\xi_i\geq0$ ，因为必有 $f(x_i)-y_i-\epsilon-\xi_i<0$ ，所以必有 $\alpha_i,\tilde{\alpha_i}=0$ 。

SVR模型的解为
$f(x)=\sum\limits_{i=1}^N(\tilde{\alpha_i}-\alpha_i)x_i\cdot x+b$
显然，能使 $(\tilde{\alpha_i}-\alpha_i)=0$ 的样本点必定落在误差间隔线上或者误差间隔外。

另外，SVR也可以使用核技巧。

3. 非线性SVM与核函数

3.1核技巧

非线性问题是指通过非线性模型才能很好地进行分类的问题，如下图所示，无法用直线（超平面）将正负实例分开，但是可以用一条椭圆曲线（超曲面）分来。

1550540810192

这个问题的解决方法是进行一个非线性变换，将非线性问题转换为线性问题，通过变换后的线性问题的方法来求解原来的非线性问题。上面的问题，原空间和新空间都是 $R^2$ ，但是经过了非线性映射的处理。更一般的，往往将低维空间的特征映射到高维空间，从而使低维的线性不可分问题转换为高维线性可分问题。

设原空间为 $，X\in R^2，x=(x_1,x_2)^T\in X$ ，新空间为 $Z\in R^2,z=(z_1,z_2)\in Z$ ，非线性映射为
$z=\phi(x)=(x_1^2,x_2^2)^T$
经过映射，原空间X变为新空间Z，原空间中的点相应变换为新空间中的点，原空间的椭圆变为新空间的直线
$w_1x_1^2+w_2x_2^2+b=0 \rightarrow w_1z_1+w_2z_2+b=0$

核技巧本质即，通过一个非线性变换将输入空间对应于一个特征空间，使得在输入空间中的超曲面模型对应于特征空间中的超平面模型。

如何理解映射和空间：在非线性映射中用基的角度讨论空间变换没有任何意义，因为任何空间中的向量用基向量进行表示，是线性表示，非线性映射不满足 $f(ax+by)=af(x)+bf(y)$ 。这里，非线性映射前后的空间采用的都是自然坐标系，真正重要的是找到映射关系（函数）。

核函数：设X是输入空间（欧式空间 $R^n$ 子集或者离散集合），又设H为特征空间（希尔伯特空间），如果存在一个从X到H的映射：
$\phi(x):X\rightarrow H$
使得对于所有的 $x,z\in X$ ，函数 $K(x,z)$ 满足
$K(x,z)=\phi(x)\cdot\phi(z)$
则称K为核函数， $\phi$ 为映射函数，其中 $\phi(x)\cdot\phi(z)$ 为内积运算。

核技巧的根本目的在于，在学习和预测中只定义核函数，而不显示地定义映射函数。因为，通常直接计算 $K(x,z)$ 比较简单，而通过映射 $\phi(x)\cdot\phi(z)$ 计算则比较困难。这里的特征空间一般是高维的，甚至是无穷维的。而且，对于给定的核函数 $K(x,z)$ ，特征空间和映射函数的取法并不唯一，可以去不同的特征空间，即便是在同一特征空间，也可以取不同的映射。

一个理解核函数由特征空间和映射函数决定的非常好地例子：

1550542695539

3.2 核技巧在SVM的应用

线性支持向量机的对偶问题中，目标函数和决策函数都只涉及输入实例与实例之间的内积。自然想到，我们将样本点经过非线性映射投射到高维空间后，使用线性支持向量机求解后，使用核技巧 $K(x_i,x_j)=\phi(x_i)\cdot\phi(x_j)$ 。可以看出，确定新特征空间、非线性映射这两步可以直接省略，给定核函数即可，至于什么样的特征空间与非线性映射能够得出我们设定的核函数，不需要关心。

此时给定核函数，目标函数转换为
$W(\alpha)=\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i\cdot x_j)-\sum\limits_{i=1}^N\alpha_i$
分类函数用核函数替换为
$f(x)=\text{sign}(\sum\limits_{j=1}^N\alpha_i^*y_i\phi(x_i)\cdot \phi(x)+b^*)=\text{sign}(\sum\limits_{i=1}^N\alpha_i^*y_iK(x_i,x)+b^*)$

这等价于经过映射函数将原来的输入空间变换到一个新的特征空间，将输入空间的内积变换为特征空间中的内积 $\phi(x_i)\cdot\phi(x_j)$ ，在新的特征空间中从训练样本中学习非线性支持向量机。

通常所说的和核函数是正定核函数，一个函数是正定核函数的充要条件如下

1550543710346

3.3 常用的核函数

多项式核函数： $K(x_i,x_j)=(x_i\cdot x_j)^d$
高斯核函数： $K(x_i,x_j)=\exp(-\frac{||x_i-x_j||^2}{2\sigma^2})$
拉普拉斯核函数： $K(x_i,x_j)=\exp(-\frac{||x_i-x_j||^2}{\sigma})$
Sigmoid核函数： $K(x_i,x_j)=\tanh(\beta x_i\cdot x_j+\theta)$

几个性质：

若 $K_1$ 和 $K_2$ 是核函数，则对于任意的正数 $\gamma_1,\gamma_2$ ，其线性组合也是核函数；
若 $K_1$ 和 $K_2$ 是核函数，则核函数的直积 $K_1(x,z)K_2(x,z)$ 也是核函数；
若 $K_1$ 是核函数，则对于任意的函数 $g(x)$ ， $K(x,z)=g(x)K_1(x,z)g(z)$ 也是核函数。

3.4 算法总结

1550545709026

3.4 核方法

前面提到，SVM和SVR模型都可以表示成核函数的线性组合，更一般的结论成为“表示定理”

表示定理：令H为核函数K对应的再生核希尔伯特空间， $||h||_H$ 表示H空间中关于h的范数，对于任意单调递增函数 $\Omega:[0,\infin]\rightarrow R$ 和任意非负损失函数 $l:R^m\rightarrow [0,\infin]$ ，优化问题

$\min\limits_{h\in H} \quad F(h)=\Omega(||h||_H)+l(h(x_1),h(x_2),\dots,h(x_N))$

解总是可以写为
$h^*(x)=\sum\limits_{i=1}^N\alpha K(x,x_i)$

注意，表示定理对损失函数没有限制，不连续、不凸都行，对正则化项仅要求单调递增，甚至不要求是凸函数，这表明对于一般的损失函数和正则化项，优化问题的解都可以表示为核函数的线性组合。