翻译: 3.4. Softmax 回归 pytorch

在第 3.1 节中，我们介绍了线性回归，在第 3.2 节中从头开始实现， 并在第 3.3节中再次使用深度学习框架的高级 API来完成繁重的工作。

当我们想要回答多少时，回归是我们解决有多少的问题。如果您想预测出售房屋的美元数（价格），或者棒球队的获胜次数，或者患者在出院前住院的天数，那么您可能寻找回归模型。

在实践中，我们更经常对分类感兴趣：问的不是“多少”而是“哪个”：
*此电子邮件是否属于垃圾邮件文件夹或收件箱？
*该客户是否更有可能注册或不注册订阅服务？
*这张图片描绘的是驴、狗、猫还是公鸡？
*阿斯顿接下来最有可能看哪部电影？

通俗地说，机器学习从业者重载了词 分类来描述两个微妙不同的问题：

• （i）我们只对将示例硬分配到类别（类）感兴趣的问题；
• (ii) 我们希望进行软分配的那些，即评估每个类别适用的概率。

这种区别往往会变得模糊，部分原因是，即使我们只关心硬分配，我们仍然使用进行软分配的模型。

3.4.1。分类问题

为了让我们的脚湿透，让我们从一个简单的图像分类问题开始。在这里，每个输入由一个2 x 2灰度图像。我们可以用单个标量表示每个像素值，给我们四个特征x1, x2, x3, x4. 此外，让我们假设每个图像属于“猫”、“鸡”和“狗”类别中的一个。

接下来，我们必须选择如何表示标签。我们有两个明显的选择。也许最自然的冲动是选择 y ∈ {1, 2, 3}, 其中整数代表 {dog, cat, chicken} 类别。这是在计算机上存储此类信息的好方法。如果类别之间有某种自然顺序，假设我们试图预测{baby, toddler, adolescent, yound adult, adult, geriatric} ，那么将这个问题转换为回归并保持这种格式的标签甚至可能是有意义的。

但是一般的分类问题并不伴随类之间的自然排序。幸运的是，统计学家很久以前就发明了一种表示分类数据的简单方法：one-hot encoding。one-hot 编码是一个向量，其分量与我们的类别一样多。对应于特定实例类别的组件设置为 1，所有其他组件设置为 0。在我们的例子中，标签y 将是一个三维向量，其中(1,0,0) 对应于“猫”，(0,1,0)“鸡”，和(0,0,1) 对“狗”：

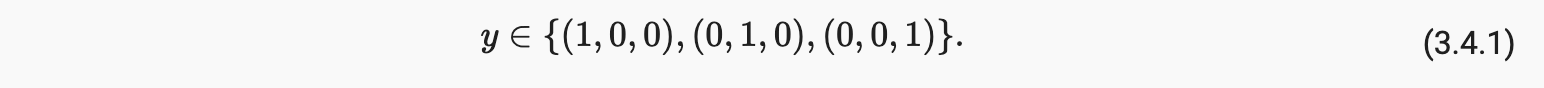
3.4.2. 网络架构

为了估计与所有可能的类别相关的条件概率，我们需要一个具有多个输出的模型，每个类别一个。为了使用线性模型进行分类，我们需要与输出一样多的仿射函数。每个输出将对应于它自己的仿射函数。在我们的例子中，由于我们有 4 个特征和 3 个可能的输出类别，我们将需要 12 个标量来表示权重（w带下标）和 3 个标量来表示偏差（b带下标）。我们计算这三个logits， o1,o2， 和o3, 对于每个输入：

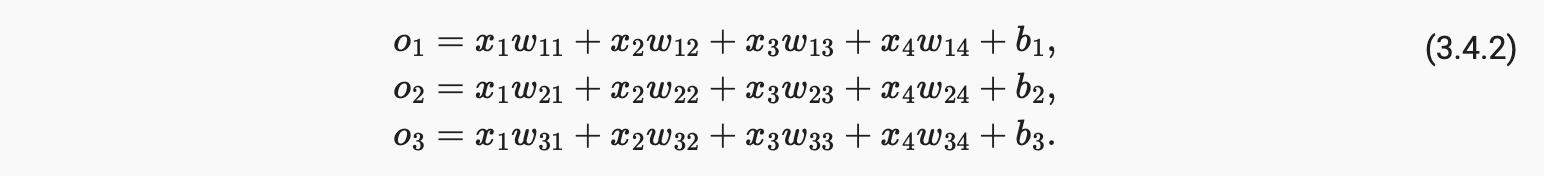
我们可以用图 3.4.1所示的神经网络图来描述这个计算 。就像在线性回归中一样，softmax 回归也是一个单层神经网络。并且由于每个输出的计算，o1，o2 和o3，取决于所有输入，x1,x2,x3， 和x4，softmax回归的输出层也可以描述为全连接层。

为了更紧凑地表达模型，我们可以使用线性代数符号。以向量形式，我们得到o = Wx + b ，一种更适合数学和编写代码的形式。请注意，我们已将所有权重收集到一个3 x 4矩阵和给定数据示例的特征x，我们的输出由我们的权重与我们的输入特征加上我们的偏差的矩阵向量乘积给出b.

3.4.3. 全连接层的参数化成本

3.4.4 Softmax 操作

我们将在这里采用的主要方法是将模型的输出解释为概率。我们将优化我们的参数以产生最大化观察数据的可能性的概率。然后，为了生成预测，我们将设置一个阈值，例如，选择具有最大预测概率的标签。

你可能会建议我们表示 logits o直接作为我们概率的输出。但是，将线性层的输出直接解释为概率存在一些问题。一方面，没有什么限制这些数字总和为 1。另一方面，根据输入，它们可以取负值。这些违反了 2.6 节中提出的基本概率公理

要将我们的输出表示为概率，我们必须保证（即使在新数据上）它们将是非负的并且总和为 1。此外，我们需要一个训练目标来鼓励模型忠实地估计概率。在分类器输出 0.5 的所有实例中，我们希望这些实例中有一半实际上属于预测类。这是一个称为校准的属性。

社会科学家 R. Duncan Luce 于 1959 年在选择模型的背景下发明的softmax 函数正是这样做的。为了将我们的 logit 转换为非负且总和为 1，同时要求模型保持可微分，我们首先对每个 logit 取幂（确保非负性），然后除以它们的总和（确保它们总和为 1）：

虽然 softmax 是非线性函数，但 softmax 回归的输出仍然是由输入特征的仿射变换决定的；因此，softmax 回归是一个线性模型。

3.4.5 小批量矢量化

3.4.6 损失函数

接下来，我们需要一个损失函数来衡量我们预测概率的质量。我们将依赖最大似然估计，这与我们在为线性回归中的均方误差目标提供概率证明时遇到的概念完全相同（第 3.1.3 节）。

3.4.6.1 似然函数

3.4.6.2 Softmax 和求导

由于 softmax 和相应的损失非常常见，因此值得更好地了解它是如何计算的。将 (3.4.3)代入 (3.4.8)中损失的定义，并使用我们得到的 softmax 的定义：

换句话说，导数是我们的模型分配的概率（由 softmax 操作表示）与实际发生的概率（由 one-hot 标签向量中的元素表示）之间的差异。从这个意义上说，它与我们在回归中看到的非常相似，其中梯度是观察值之间的差异y并估计y’
. 这不是巧合。在任何指数族（参见关于分布的在线附录）模型中，对数似然的梯度正是由该项给出。这一事实使计算梯度在实践中变得容易。

3.4.6.3 交叉熵损失

现在考虑这样一种情况，我们不仅观察到单个结果，而且观察到结果的整个分布。我们可以对标签使用与以前相同的表示y. 唯一的区别是，而不是只包含二进制条目的向量(0,0,1) ，我们现在有一个通用的概率向量，比如说(0.1,0.2,0.7) . 我们之前用来定义损失的变量l在（3.4.8）中仍然可以正常工作，只是解释稍微更笼统。它是标签分布的损失的期望值。这种损失称为交叉熵损失，它是分类问题中最常用的损失之一。我们可以通过介绍信息论的基础知识来揭开这个名字的神秘面纱。如果您想了解更多信息论的细节，您可以进一步参考信息论的在线附录。

3.4.7 信息论基础

信息论处理以尽可能简洁的形式编码、解码、传输和操作信息（也称为数据）的问题。

3.4.7.1 熵

信息论的中心思想是量化数据中的信息内容。这个数量限制了我们压缩数据的能力。在信息论中，这个量称为 分布的熵P, 它由以下等式捕获：

3.4.7.2 意外Surprisal

您可能想知道压缩与预测有什么关系。想象一下，我们有一个要压缩的数据流。如果我们总是很容易预测下一个令牌，那么这个数据很容易压缩！举一个极端的例子，流中的每个标记总是取相同的值。那是一个非常无聊的数据流！而且不仅无聊，而且还很容易预测。因为它们总是相同的，所以我们不必传输任何信息来传达流的内容。易于预测，易于压缩。

3.4.7.3 重新审视交叉熵

简而言之，我们可以从两个方面考虑交叉熵分类目标：

• （i）最大化观察数据的可能性；
• (ii) 尽量减少我们传达标签所需的意外Surprisal（以及比特数）。

3.4.8 模型预测与评估

在训练了 softmax 回归模型之后，给定任何示例特征，我们可以预测每个输出类的概率。通常，我们使用具有最高预测概率的类作为输出类。如果预测与实际类（标签）一致，则预测是正确的。在实验的下一部分，我们将使用准确率来评估模型的性能。这等于正确预测数与预测总数之间的比率。

3.4.9。概括

• softmax 操作采用一个向量并将其映射为概率。

• Softmax 回归适用于分类问题。它使用softmax操作中输出类的概率分布。

• 交叉熵可以很好地衡量两个概率分布之间的差异。它测量给定模型对数据进行编码所需的位数。

3.4.10 练习

参考

https://d2l.ai/chapter_linear-networks/softmax-regression.html