《机器学习》------实验一（回归）

企业开发 2022-03-29 09:13:29 阅读次数: 0

问题一：

对于线性回归问题，给定：

w 0 ∗ = ( 1 n ∑ i y i ) − w 1 ∗ ( 1 n ∑ i x i ) (1) \begin{aligned} w^*_0&=\left(\frac{1}{n}\sum_iy_i\right)-{w_1^*}\left(\frac{1}{n}\sum_ix_i\right) \\ \end{aligned}\tag{1} w0∗​​=(n1​i∑​yi​)−w1∗​(n1​i∑​xi​)​(1)
w 1 ∗ = − ∑ i x i ( w 0 ∗ − y i ) / ∑ i x i 2 (2) \begin{aligned} {w_1^*}&=-\sum_ix_i({w_0^*}-y_i)/ \sum_ix_i^2 \end{aligned}\tag{2} w1∗​​=−i∑​xi​(w0∗​−yi​)/i∑​xi2​​(2)

试推导：
w 1 ∗ = ∑ i y i ( x i − 1 n ∑ i x i ) ∑ i x i 2 − 1 n ( ∑ i x i ) 2 \begin{aligned} {w_1^*}=\frac{\sum_iy_i(x_i-\frac{1}{n}\sum_ix_i)}{\sum_ix_i^2-\frac{1}{n}(\sum_ix_i)^2} \end{aligned} w1∗​=∑i​xi2​−n1​(∑i​xi​)2∑i​yi​(xi​−n1​∑i​xi​)​​

解:
把（1）式代入（2）式为：

w 1 ∗ = − ∑ i x i ( 1 n ∑ i y i − w 1 ∗ 1 n ∑ i x i − y i ) ∑ i x i 2 w 1 ∗ ∑ i x i 2 = − ∑ i x i ( 1 n ∑ i y i − w 1 ∗ 1 n ∑ i x i − y i ) w 1 ∗ ∑ i x i 2 = − ∑ i x i ( 1 n ∑ i y i ) + w 1 ∗ ( ∑ i x i ) 2 + ∑ i x i ( y i ) w 1 ∗ ( ∑ i x i 2 − 1 n ∑ i x i ) = ∑ i y i ( x i − 1 n ∑ i x i ) w 1 ∗ = ∑ i y i ( x i − 1 n ∑ i x i ) ∑ i x i 2 − 1 n ( ∑ i x i ) 2 \begin{aligned} {w_1^*}&=\frac{-\sum_ix_i(\frac{1}{n}\sum_iy_i-{w_1^*}\frac{1}{n}\sum_ix_i-y_i)}{\sum_ix_i^2}\\ {w_1^*}\sum_ix_i^2 &=-\sum_ix_i(\frac{1}{n}\sum_iy_i-{w_1^*}\frac{1}{n}\sum_ix_i-y_i)\\ {w_1^*}\sum_ix_i^2 &=-\sum_ix_i(\frac{1}{n}\sum_iy_i)+{w_1^*}(\sum_ix_i)^2+\sum_ix_i(y_i)\\ {w_1^*}(\sum_ix_i^2-\frac{1}{n}\sum_ix_i) &=\sum_iy_i(x_i-\frac{1}{n}\sum_ix_i)\\ {w_1^*} &=\frac{\sum_iy_i(x_i-\frac{1}{n}\sum_ix_i)}{\sum_ix_i^2-\frac{1}{n}(\sum_ix_i)^2} \end{aligned} w1∗​w1∗​i∑​xi2​w1∗​i∑​xi2​w1∗​(i∑​xi2​−n1​i∑​xi​)w1∗​​=∑i​xi2​−∑i​xi​(n1​∑i​yi​−w1∗​n1​∑i​xi​−yi​)​=−i∑​xi​(n1​i∑​yi​−w1∗​n1​i∑​xi​−yi​)=−i∑​xi​(n1​i∑​yi​)+w1∗​(i∑​xi​)2+i∑​xi​(yi​)=i∑​yi​(xi​−n1​i∑​xi​)=∑i​xi2​−n1​(∑i​xi​)2∑i​yi​(xi​−n1​∑i​xi​)​​

问题二：

对于线性回归问题，给定：
arg min ⁡ w 0 , w 1 L ( w ^ ) = ∥ y − X w ^ ∥ 2 \begin{aligned} \argmin_{\mathbf{w_0,w_1}}\mathcal{L}(\mathbf{\hat{w}})=\|y-X\mathbf{\hat{w}}\|^2 \end{aligned} w0​,w1​argmin​L(w^)=∥y−Xw^∥2​

试推导：
w ^ = ( X T X ) − 1 X T y \mathbf{\hat{w}}=(X^TX)^{-1}X^Ty w^=(XTX)−1XTy

解：

∥ y − X w ^ ∥ 2 = ( X w ^ − y ) T ( X w ^ − y ) = ( w ^ T X T − y T ) ( X w ^ − y ) = w ^ T X T X w ^ − w ^ T X T y − y T X w ^ + y T y \begin{aligned}\|y-X\mathbf{\hat{w}}\|^2 &=(X\mathbf{\hat{w}}-y)^T(X\mathbf{\hat{w}}-y)\\ &=(\mathbf{\hat{w}}^TX^T-y^T)(X\mathbf{\hat{w}}-y)\\ &=\mathbf{\hat{w}}^TX^TX\mathbf{\hat{w}}-\mathbf{\hat{w}}^TX^Ty-y^TX\mathbf{\hat{w}}+y^Ty \end{aligned} ∥y−Xw^∥2​=(Xw^−y)T(Xw^−y)=(w^TXT−yT)(Xw^−y)=w^TXTXw^−w^TXTy−yTXw^+yTy​

令：

f ( w ^ ) = w ^ T X T X w ^ − w ^ T X T y − y T X w ^ + y T y \begin{aligned} f(\mathbf{\hat{w}})&=\mathbf{\hat{w}}^TX^TX\mathbf{\hat{w}}-\mathbf{\hat{w}}^TX^Ty-y^TX\mathbf{\hat{w}}+y^Ty \end{aligned} f(w^)​=w^TXTXw^−w^TXTy−yTXw^+yTy​

f ( w ^ ) f(\mathbf{\hat{w}}) f(w^) 对 w ^ \mathbf{\hat{w}} w^ 求偏导为：
d f d w ^ = X T X w ^ + ( w ^ T X T X ) T − X T y − X T y = X T X w ^ + X T X w ^ − X T y − X T y = 2 X T X w ^ − 2 X T y \begin{aligned} \frac{df}{d\mathbf{\hat{w}}}&=X^TX\mathbf{\hat{w}}+(\mathbf{\hat{w}}^TX^TX)^T-X^Ty-X^Ty\\ &=X^TX\mathbf{\hat{w}}+X^TX\mathbf{\hat{w}}-X^Ty-X^Ty\\ &=2X^TX\mathbf{\hat{w}}-2X^Ty \end{aligned} dw^df​​=XTXw^+(w^TXTX)T−XTy−XTy=XTXw^+XTXw^−XTy−XTy=2XTXw^−2XTy​

令 d f d w ^ = 0 \frac{df}{d\mathbf{\hat{w}}}=0 dw^df​=0：
w ^ = ( X T X ) − 1 X T y \mathbf{\hat{w}}=(X^TX)^{-1}X^Ty w^=(XTX)−1XTy

问题三：

  1. 构造人工数据。提示：（ x , y x,y x,y ）要呈线性分布。
  2. 利用公式1和公式2求出直线方程。
  3. 评价两种方法的优劣（运行时间、目标函数等）
  4. 画图。（画出原始数据点云、直线）

1、构造人工数据：

datMat = np.matrix(
       [[ 1.,],
        [ 2.,],
        [ 3.,],
        [ 3.,],
        [ 5.,],
        [ 6.,],
        ])

classLabels = [3.09, 5.06,.03, 9.12, 10.96,6.4,]

2、公式1函数：

# 公式1：一元回归
def Linear_Regression1(dataArr,classLabels):

    Denominator = 0.0 # 分母
    molecular = 0.0 # 分子
    w=0.0
    b=0.0

    for i in range(len(dataArr)):
        molecular += classLabels[i]* (dataArr[i] - average(dataArr))
        Denominator += (dataArr[i]-average(dataArr))**2

    w=molecular/Denominator
    b=average(classLabels)-w*average(dataArr)
    return w,b

公式2函数：

# 公式2：多元回归
def Linear_Regression2(dataArr,classLabels):

    # 建立一列为1的矩阵
    a=np.matrix(np.ones((len(classLabels),1)))
    # print(a)
    # 在原始数据矩阵上加一列1
    datMat=np.c_[dataArr,a]
    # print(datMat)
    classLabels = np.asmatrix(classLabels).reshape(-1, 1)# 把数组转化为1列矩阵

    # print(classLabels)
    # w=np.linalg.inv((dataArr.T*dataArr))*dataArr.T*classLabels
    w = (datMat.T * datMat).I * datMat.T * classLabels # .I 表示矩阵的逆
    w_0=w[0]
    w_1=w[1]
    return w_0,w_1

损失函数：

def lossFunction(y, y_hat):
    '''
    损失函数模块
    '''
    n = len(y)
    sum = 0
    for i in range(n):
        sum += pow((y[i] - y_hat[i]), 2)
    # 损失函数定义为 MSE/2
    L = (sum) / (2 * n)
    return L

3、两种方法比较：

方法 运行时间 目标函数（损失） 方法
第1种（一维） 0.000974 4.984367 最小二乘法
第2种（二维） 0.000160 因为得到w和，b一样的所以损失也是一样的 最小二乘法

4、运行结果：

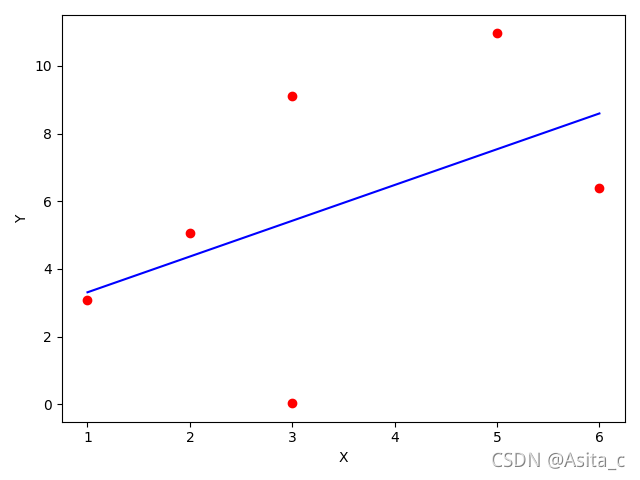
在这里插入图片描述
5、图像：
在这里插入图片描述
作业四：

  • 构造二维人工数据
    提示：正负样本可用直线分离，标记好类别。并对数据集进行拆分（训练集和测试集）。

  • 利用梯度下降法和牛顿法实现逻辑回归算法。
    评价两种方法的优劣（运行时间、收敛次数等）

  • 对测试集中的样本进行分类，并计算错误率

  • 画图（画出训练集、直线、以及测试集）

1、构造人工数据集：
前两列的属性，最后一列是标签：

datMat = np.matrix([
        [ 0.33,-1.8,1],
        [ -0.75,-0.47,0],
        [ -0.94,-3.79,1],
        [ -0.87,1.9,1],
        [ 0.95,-4.34,0],
        [ 0.36,4.27,0],
        [ -0.83,1.32,1],
        [ 0.28,-2.13,0],
        [ -0.9,1.84,1],
        [ -0.76,3.47,0],
        [ -0.01,4.0,1],
        ])

拆分数据集为训练集和测试集：

train_x=datMat[0:5,0:2]
    train_y=datMat[0:5,2]
    test_x=datMat[6:11:,0:2]

    test_y=datMat[6:11,2]

2、梯度下降法实现逻辑回归算法：

# 逻辑回归迭代过程：批量梯度下降法：
def Logistic_Regression(X, y, stepsize, max_iters):
    intercept = np.ones((X.shape[0], 1))  # 初始化截距为1
    X = np.concatenate(( X,intercept), axis=1)# 数组拼接
    # print(X)
    m, n = X.shape
    w = np.zeros((n,1))  # 初始化参数为0
    J = pd.Series(np.arange(max_iters, dtype=float))  # 损失函数
    # print("w", w)
    # print("x",X)
    # iter_count = 0  # 当前迭代次数
    # print("y", y)
    # print("y", type(y))

    count=0
    # \sum_i(Sigmoid(wx)-y)*x
    for i in range(max_iters):  # 梯度下降迭代

        z = np.dot(X, w)  # 线性函数
        # print("z\n",z)
        h = sigmoid(z)
        # print("h",type(h))
        g = gradient(X, h, y)  # 计算梯度

        # print("g\n",g)
        w -= stepsize * g # 更新参数

        # l = loss(h, y)  # 计算更新后的损失
        J[i] = -stepsize*np.sum(y.T*np.log(h)+(1-y).T*np.log(1-h)) #计算损失函数值
        count+=1

    return J, w,count  # 返回迭代后的损失和参数和迭代次数

3、牛顿法的实现代码暂时还没有去学习研究

---但牛顿和梯度下降法的主要区别就是梯度下降的方向，梯度下降法的下降方向是梯度的负方向，
但是会有锯齿现像产生，而牛顿法是在梯度下降方向上做了一定的修正，加了一个海瑟矩阵。

4、分类结果：
在这里插入图片描述
这里的迭代次数设置为10，如果再高就会导致log中为0的错误。

5、图像：

数据集设置有点抠门了，数量跟数值都小了，可能训练集和测试集稍微看起区别较小，后面后整个的图像

训练集图像：
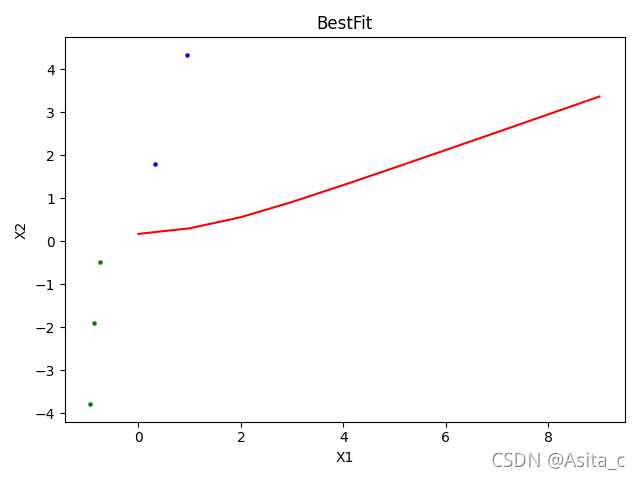
在这里插入图片描述

测试集图像：
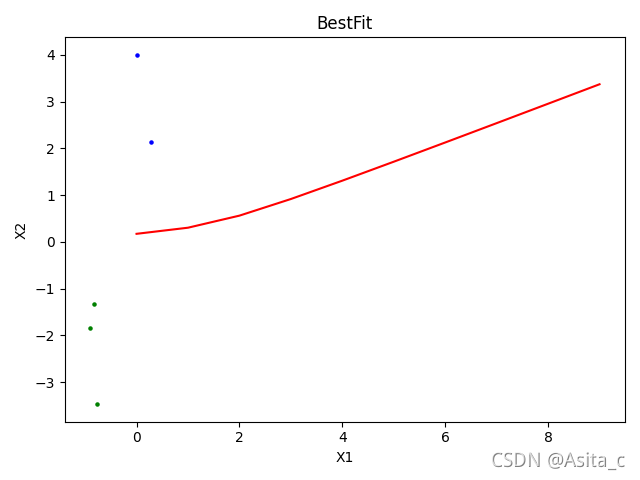
在这里插入图片描述
整个数据集分类图像：
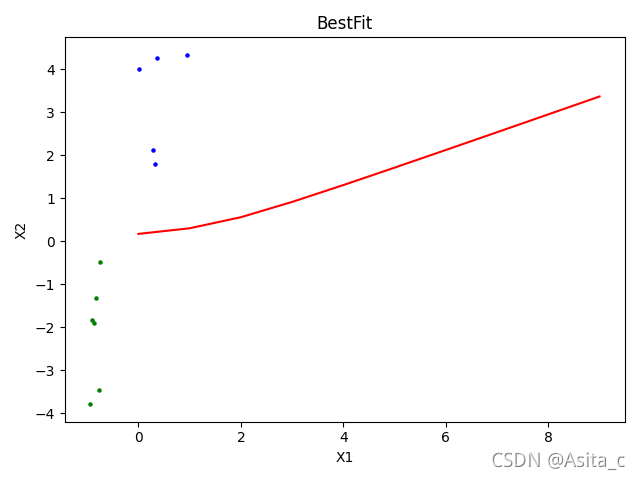
在这里插入图片描述

线性回归完整代码（包含一元线性回归和多元线性回归）：

#作   者：Asita
#开发时间：2021/11/10 23:11

# 给定一维数据集：
import time
import numpy as np
import matplotlib.pyplot as plt

datMat = np.matrix([
        [ 1.,],
        [ 2.,],
        [ 3.,],
        [ 3.,],
        [ 5.,],
        [ 6.,],
        ])

classLabels = [3.09, 5.06,.03, 9.12, 10.96,6.4,]

def average(data):
    sum = 0
    num = len(data)
    for i in range(num):
        sum += data[i]
    return sum / num

# 泛化的式子
def linearRegressionModule(x, a, b):
    """
    线性回归模块
    """
    y_hat = a * x + b
    return y_hat

def lossFunction(y, y_hat):
    '''
    损失函数模块
    '''
    n = len(y)
    sum = 0
    for i in range(n):
        sum += pow((y[i] - y_hat[i]), 2)
    # 损失函数定义为 MSE/2
    L = (sum) / (2 * n)
    return L

# 公式1：一元回归
def Linear_Regression1(dataArr,classLabels):

    Denominator = 0.0 # 分母
    molecular = 0.0 # 分子

    for i in range(len(dataArr)):
        molecular += classLabels[i]* (dataArr[i] - average(dataArr))
        Denominator += (dataArr[i]-average(dataArr))**2

    w=molecular/Denominator
    b=average(classLabels)-w*average(dataArr)
    return w,b


# 公式2：多元回归
def Linear_Regression2(dataArr,classLabels):


    # print(a)
    # 在原始数据矩阵上加一列1(法1):
    # 建立一列为1的矩阵
    # a=np.matrix(np.ones((len(classLabels),1)))
    # datMat=np.c_[dataArr,a]
    # print(datMat)X

    # 法2：
    intercept = np.ones((dataArr.shape[0], 1))  # 初始化截距为1
    X = np.concatenate((intercept, dataArr), axis=1)  # 数组拼接

    classLabels = np.asmatrix(classLabels).reshape(-1, 1)# 把数组转化为1列矩阵

    # print(classLabels)
    # w=np.linalg.inv((dataArr.T*dataArr))*dataArr.T*classLabels
    w = (X.T * X).I * X.T * classLabels # .I 表示矩阵的逆
    w_0=w[0]
    w_1=w[1]
    return w_0,w_1

def showDataSet(dataMat,classLabels,w,b):
    """
    数据可视化
    Parameters:
        dataMat - 数据矩阵
        labelMat - 数据标签
    Returns:
        无
    """
    data_x = []
    data_y = []
    line_y=[]
    plt.xlabel('X')
    # 设置Y轴标签
    plt.ylabel('Y')
    for i in range(len(dataMat)):
        data_x.append(dataMat[i])
        line_y.append(w*datMat[i]+b)

    for j in range(len(classLabels)):
        data_y.append(classLabels[j])

    data_x1 = np.array(data_x)
    data_y1 = np.array(data_y)
    line_y1=np.array(line_y)
    plt.scatter(data_x1, data_y1, c='r', marker='o')

    plt.plot(data_x1[:,0],line_y1[:,0],c='b')
    plt.show()



if __name__ == '__main__':

    start_time = time.time()  # 记录程序开始运行时间
    for i in range(1000):
        w, b = Linear_Regression1(datMat, classLabels)
    end_time = time.time()  # 记录程序结束运行时间
    time1=(end_time-start_time)/1000
    print('first algorithm  Took %f seconds' % time1)

    if b>0:
        print('the line is y=%f*x+%f' % (w, b))
    else:
        print('the line is y=%f*x%f' % (w, b))

    showDataSet(datMat,classLabels,w,b)

    print("---------------------------------------")
    start_time1 = time.time()  # 记录程序开始运行时间
    for i in range(1000):
        w_0,w_1= Linear_Regression2(datMat, classLabels)
    end_time1 = time.time()  # 记录程序结束运行时间
    time2=(end_time1 - start_time1)/1000
    print('second algorithm  Took %f seconds' % time2)
    print(w_0)
    print(w_1)

    # 计算损失：
    y_hat = np.ones(len(datMat))
    for i in range(len(datMat)):
        y_hat[i] = datMat[i] * w + b

    l1 = lossFunction(y_hat, classLabels)

    print('loss is %f'%l1)

Logistics回归完整代码：

#作   者：Asita
#开发时间：2021/11/11 16:11

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
datMat = np.matrix([
        [ 0.33,1.8,0],
        [ -0.75,-0.47,1],
        [ -0.94,-3.79,1],
        [ -0.87,-1.9,1],
        [ 0.95,4.34,0],
        [ 0.36,4.27,0],
        [ -0.83,-1.32,1],
        [ 0.28,2.13,0],
        [ -0.9,-1.84,1],
        [ -0.76,-3.47,1],
        [ 0.01,4.0,0],
        ])


def sigmoid(x):
    sigmoid=1.0/(1.0+np.exp(-x))
    return sigmoid

#损失：
# y=classLabels
def loss(h,y):
    loss=(-y*np.log(h)-(1-y)*np.log(1-h)).mean()

    return loss

# 计算梯度: log(p/(1-p))=wx
def gradient(X,h,y):
    gradient=np.dot(X.T,(y-h))
    # print("gradient",gradient)
    return gradient


# 逻辑回归迭代过程：批量梯度下降法：
def Logistic_Regression(X, y, stepsize, max_iters):
    intercept = np.ones((X.shape[0], 1))  # 初始化截距为1
    X = np.concatenate(( X,intercept), axis=1)# 数组拼接
    # print(X)
    m, n = X.shape
    w = np.zeros((n,1))  # 初始化参数为0
    J = pd.Series(np.arange(max_iters, dtype=float))  # 损失函数
    # print("w", w)
    # print("x",X)
    # iter_count = 0  # 当前迭代次数
    # print("y", y)
    # print("y", type(y))

    count=0
    # \sum_i(Sigmoid(wx)-y)*x
    for i in range(max_iters):  # 梯度下降迭代

        z = np.dot(X, w)  # 线性函数
        # print("z\n",z)
        h = sigmoid(z)
        # print("h",type(h))
        g = gradient(X, h, y)  # 计算梯度

        # print("g\n",g)
        w -= stepsize * g # 更新参数

        # l = loss(h, y)  # 计算更新后的损失
        J[i] = -stepsize*np.sum(y.T*np.log(h)+(1-y).T*np.log(1-h)) #计算损失函数值
        count+=1

    return J, w,count  # 返回迭代后的损失和参数

#逻辑回归预测函数：
def Logistic_Regression_predict(test_X,test_label,w):
    intercept=np.ones((test_X.shape[0],1))
    test_X=np.concatenate((intercept,test_X),axis=1)
    predict_z=np.dot(test_X,w)
    predict_label=sigmoid(-predict_z)
    predict_label[predict_label<0.5]=0
    predict_label[predict_label>0.5]=1
    return predict_label





def plotBestFit(J,dataMat,labelMat):
    """
    绘制图形
    :param wb: 回归系数
    :param dataMat: 输入数据集
    :param labelMat: 类别标签
    :return: 无
    """
    import matplotlib.pyplot as plt
    dataArr=np.array(dataMat)
    n=np.shape(dataArr)[0]      #获取数据集的行数
    x1=[];y1=[];x2=[];y2=[]
    for i in range(n):
        if int(labelMat[i])==1:
            x1.append(dataArr[i,0])
            y1.append(dataArr[i,1])
        else:
            x2.append(dataArr[i, 0])
            y2.append(dataArr[i, 1])

    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.scatter(x1,y1,s=5,c="green")
    ax.scatter(x2,y2,s=5,c="blue")


    J.plot(c="red")
    plt.title('BestFit')  # 绘制title
    plt.xlabel('X1');
    plt.ylabel('X2')  # 绘制label
    plt.show()



if __name__ == '__main__':

    train_x=datMat[0:5,0:2]
    train_y=datMat[0:5,2]
    test_x=datMat[6:11:,0:2]

    test_y=datMat[6:11,2]
    datMat_all=datMat[:,0:2]
    class_all=datMat[:,2]

    # print(train_x)
    # print("----------------------")
    # print(train_y)
    # print("----------------------")

    l,w,count=Logistic_Regression(train_x,train_y,0.05,10)
    # print(w)
    # 图像：
    plotBestFit(l,datMat_all,class_all)
    print("迭代次数：",count)
    predict=Logistic_Regression_predict(test_x,test_y,w)
    print("w:\n",w)
    print("测试集标签test_y\n",test_y)
    print("predict\n",predict)
    accuracy=(predict==test_y).mean()
    print("accuracy:",accuracy)

猜你喜欢

转载自blog.csdn.net/Naruto_8/article/details/121169319
今日推荐
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
GCC 14.1 发布
面壁智能发布 Eurux-8x22B 开源大模型 —— 堪称「理科状元」
开源日报 | 谷歌扶持鸿蒙上位；开源Rabbit R1；Docker加持的安卓手机；微软的焦虑和野心；海尔电器把开放平台关了
中国码农的“35岁魔咒”
蘭雅 CorelDRAW 插件 2024.5.1 国际劳动节版，免费下载
Arc Browser for Windows 1.0 正式 GA
90后程序员开发视频搬运软件、不到一年获利超 700 万，结局很刑！
周排行
Java自定义时间格式
同步整形电路
在开发中最最最常用的字符串的属性大集合
Linux 查看端口占用并杀掉
Java基础四：ArrayList
多线程之死锁就是这么简单
mysql 基础命令集
awk 命令详解
Centos6.3编译安装nginx+php步骤
OCR （Optical Character Recognition，光学字符识别）
每日归档
更多
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)
2024-05-03(19)
2024-05-02(0)
2024-05-01(4)
2024-04-30(1)
2024-04-29(40)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022