3D Coordinate Systems
Coordinates
3D space: Fix a reference point, call it origin O O O. Three directed lines through the origin, called coordinate axes. Need 3 numbers to describe the location of one point. We use R 3 R^3 R3 to denote 3D space.
R 3 = { ( x , y , z ) : x , y , z ∈ R } R^3 = \{(x,y,z): x,y,z\in R\} R3={
(x,y,z):x,y,z∈R}
We normally use the right hand rule to construct the coordinates.

Say a vector p = < a , b , c > p = <a,b,c> p=<a,b,c> represent the location of point P P P. a is the distance of p to yz-plane; b is the distance of p to xz-plane; c is the distance of p to xy-plane.
Geometric Objects
-
z = 3 z=3 z=3
this is a plane
-
x 2 + y 2 = 1 , z = 3 x^2+y^2=1, z=3 x2+y2=1,z=3
a circle at z of 3
-
x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1
a sphere
-
x 2 + y 2 = 1 , z = 3 x^2+y^2=1, z=3 x2+y2=1,z=3
a column
Distance Formula
We have two points: P 1 = < x 1 , y 1 , z 1 > P_1 = <x_1, y_1, z_1> P1=<x1,y1,z1> and P 2 = < x 2 , y 2 , z 2 > P_2 = <x_2, y_2, z_2> P2=<x2,y2,z2>.
∣ P 1 P 2 ∣ = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 |P_1P_2| = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2} ∣P1P2∣=(x1−x2)2+(y1−y2)2+(z1−z2)2
e.x:
- describe the points that have distance 1 to the origin.
x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1
- given the equation x 2 + y 2 + z 2 + 4 x − 6 y + 2 z + 6 = 0 x^2+y^2+z^2+4x-6y+2z+6=0 x2+y2+z2+4x−6y+2z+6=0, what is it the object?
( x + 2 ) 2 + ( y − 3 ) 2 + ( z + 1 ) 2 = 8 (x+2)^2+(y-3)^2+(z+1)^2=8 (x+2)2+(y−3)2+(z+1)2=8, collection of points P whose distance to point A = ( − 2 , 3 , − 1 ) A=(-2,3,-1) A=(−2,3,−1) is 2 2 2\sqrt 2 22.
Vector
Intro
Say we have two points. P 1 = < x 1 , y 1 , z 1 > P_1 = <x_1, y_1, z_1> P1=<x1,y1,z1> and P 2 = < x 2 , y 2 , z 2 > P_2 = <x_2, y_2, z_2> P2=<x2,y2,z2>. We use a vector to represent the distance P 1 P 2 ⃗ = < x 2 − x 1 , y 2 − y 1 , z 2 − z 1 > \vec{P_1P_2} = <x_2-x_1, y_2-y_1, z_2-z_1> P1P2=<x2−x1,y2−y1,z2−z1>.
Addition and Scalar Multiplication
We define the addition of two vectors to be element-wise addition. For subtraction, we just pretend to add the negative direction of the second vector.
The geometric interpretation is as follows.
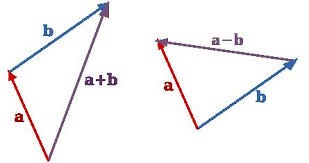
One interesting property of vector addition is commutative law.
u ⃗ + v ⃗ = v ⃗ + u ⃗ \vec u + \vec v = \vec v + \vec u u+v=v+u
For a scalar c ∈ R c \in R c∈R, and a vector u ⃗ = < u 1 , u 2 , u 3 > \vec u = <u_1, u_2, u_3> u=<u1,u2,u3>, we define c u ⃗ = < c u 1 , c u 2 , c u 3 > c \vec u = <cu_1, cu_2, cu_3> cu=<cu1,cu2,cu3>.
Magnitude
When the length and the direction of two vectors are the same, we say these two vectors are the same.
The length of a vector v v v is
∣ v ⃗ ∣ = a 2 + b 2 + c 2 |\vec{v}| = \sqrt{a^2 + b^2 + c^2} ∣v∣=a2+b2+c2
It is the distance |OP|.
Properties and Linear Combinations
For a scalar c , d ∈ R c,d \in R c,d∈R, and a vector u ⃗ , v ⃗ , w ⃗ \vec u, \vec v, \vec w u,v,w.
u ⃗ + v ⃗ = v ⃗ + u ⃗ u ⃗ + ( v ⃗ + w ⃗ ) = ( v ⃗ + u ⃗ ) + w ⃗ c ( u ⃗ + v ⃗ ) = c v ⃗ + c u ⃗ ( c + d ) u ⃗ = c u ⃗ + d u ⃗ ( c d ) u ⃗ = c ( d u ⃗ ) \vec u + \vec v = \vec v + \vec u \\\\ \vec u + (\vec v + \vec w) = (\vec v + \vec u) + \vec w \\\\ c(\vec u + \vec v) = c\vec v + c\vec u \\\\ (c+d) \vec u = c\vec u + d\vec u \\\\ (cd) \vec u = c(d\vec u) u+v=v+uu+(v+w)=(v+u)+wc(u+v)=cv+cu(c+d)u=cu+du(cd)u=c(du)
We define three basis vectors.
i ⃗ = < 1 , 0 , 0 > j ⃗ = < 0 , 1 , 0 > k ⃗ = < 0 , 0 , 1 > \vec i = <1,0,0> \\\\ \vec j = <0,1,0> \\\\ \vec k = <0,0,1> \\\\ i=<1,0,0>j=<0,1,0>k=<0,0,1>
Every vector in 3d space can be written as a linear combination of these 3 vectors. For vector u ⃗ = < u 1 , u 2 , u 3 > \vec u = <u_1, u_2, u_3> u=<u1,u2,u3>
u ⃗ = u 1 i ⃗ + u 2 j ⃗ + u 3 k ⃗ \vec u = u_1 \vec i + u_2 \vec j + u_3 \vec k u=u1i+u2j+u3k
Unit Vector
If the length of a vector is 1, then it is a unit vector.
For a given vector (not the zero vector), we can get its unit vector by doing
u ⃗ ∣ u ⃗ ∣ \frac {\vec u} {|\vec u|} ∣u∣u
Application in Physics
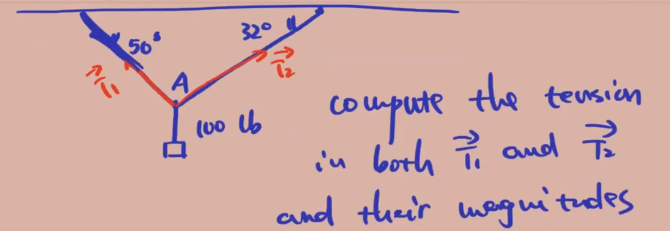
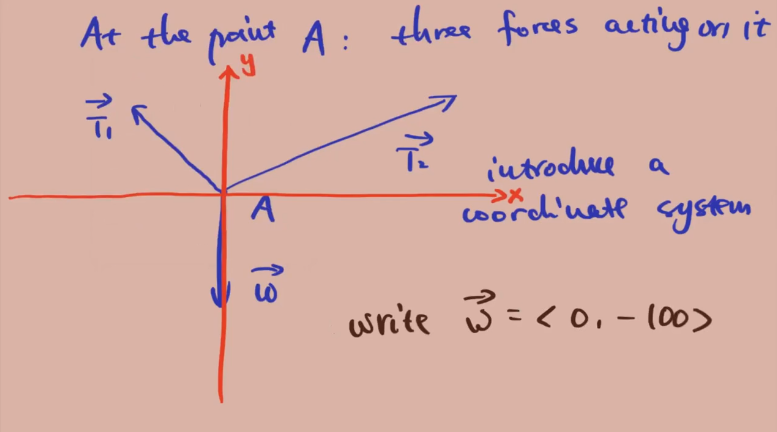
Let T ⃗ 1 = < x 1 , y 1 > \vec T_1 = <x_1, y_1> T1=<x1,y1> and T ⃗ 2 = < x 2 , y 2 > \vec T_2 = <x_2, y_2> T2=<x2,y2>.
x 1 + x 2 = 0 y 1 + y 2 = 100 y 1 / x 1 = − t a n ( 50 ) y 2 / x 2 = t a n ( 32 ) x_1 + x_2 = 0 \\\\ y_1 + y_2 = 100 \\\\ y_1/x_1 = -tan(50) \\\\ y_2/x_2 = tan(32) x1+x2=0y1+y2=100y1/x1=−tan(50)y2/x2=tan(32)
Dot Product
Properties
Give vector u ⃗ = < u 1 , u 2 , u 3 > \vec u = <u_1, u_2, u_3> u=<u1,u2,u3>, v ⃗ = < v 1 , v 2 , v 3 > \vec v = <v_1, v_2, v_3> v=<v1,v2,v3>, and w ⃗ \vec w w
u ⃗ ⋅ v ⃗ = u 1 v 1 + u 2 v 2 + u 3 v 3 u ⃗ ⋅ v ⃗ = v ⃗ ⋅ u ⃗ u ⃗ ⋅ ( v ⃗ + w ⃗ ) = u ⃗ ⋅ v ⃗ + u ⃗ ⋅ w ⃗ \vec u \cdot \vec v = u_1v_1 + u_2 v_2 + u_3v_3 \\\\ \vec u \cdot \vec v = \vec v \cdot \vec u \\\\ \vec u \cdot (\vec v + \vec w) = \vec u \cdot \vec v + \vec u \cdot \vec w u⋅v=u1v1+u2v2+u3v3u⋅v=v⋅uu⋅(v+w)=u⋅v+u⋅w
Geometric Meaning
u ⃗ ⋅ v ⃗ = ∣ u ⃗ ∣ ∣ v ⃗ ∣ c o s θ \vec u \cdot \vec v = |\vec u||\vec v| cos\theta u⋅v=∣u∣∣v∣cosθ
Two non-zero vectors are perpendicular to each other if they form an angle of π / 2 \pi/2 π/2. Algebraically, their inner product is 0.
The scalar project of u ⃗ \vec u u onto v ⃗ \vec v v is
∣ u ⃗ ∣ c o s θ = u ⃗ ⋅ v ⃗ ∣ v ⃗ ∣ |\vec u| cos \theta =\vec u \cdot \frac {\vec v} {|\vec v|} ∣u∣cosθ=u⋅∣v∣v
The vector project of u ⃗ \vec u u onto v ⃗ \vec v v is
p r o j v ⃗ ∣ u ⃗ ∣ = ( u ⃗ ⋅ v ⃗ ∣ v ⃗ ∣ ) v ⃗ ∣ v ⃗ ∣ proj_{\vec v} |\vec u| = (\vec u \cdot \frac {\vec v} {|\vec v|}) \frac {\vec v} {|\vec v|} projv∣u∣=(u⋅∣v∣v)∣v∣v
Cross Product
Motivation
Outer product, wedge product, cross product all mean the same thing.
Give vector a ⃗ = < a 1 , a 2 , a 3 > \vec a = <a_1, a_2, a_3> a=<a1,a2,a3> and b ⃗ = < b 1 , b 2 , b 3 > \vec b = <b_1, b_2, b_3> b=<b1,b2,b3>, find a vector c ⃗ \vec c c that is perpendicular to these two vectors.
a 1 c 1 + a 2 c 2 + a 3 c 3 = 0 b 1 c 1 + b 2 c 2 + b 3 c 3 = 0 a_1c_1 + a_2c_2 + a_3c_3 = 0 \\\\ b_1c_1 + b_2c_2 + b_3c_3 = 0 a1c1+a2c2+a3c3=0b1c1+b2c2+b3c3=0
Scale the first equation by b 3 b_3 b3 and the second one by a 3 a_3 a3
( a 1 b 3 − a 3 b 1 ) c 1 + ( a 2 b 3 − a 3 b 2 ) c 2 = 0 (a_1b_3 - a_3b_1)c_1 + (a_2b_3- a_3b_2)c_2 = 0 (a1b3−a3b1)c1+(a2b3−a3b2)c2=0
Find one possible solution
< c 1 , c 2 , c 3 > = < a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 > <c_1, c_2, c_3> = <a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1> <c1,c2,c3>=<a2b3−a3b2,a3b1−a1b3,a1b2−a2b1>
A more formal definition is
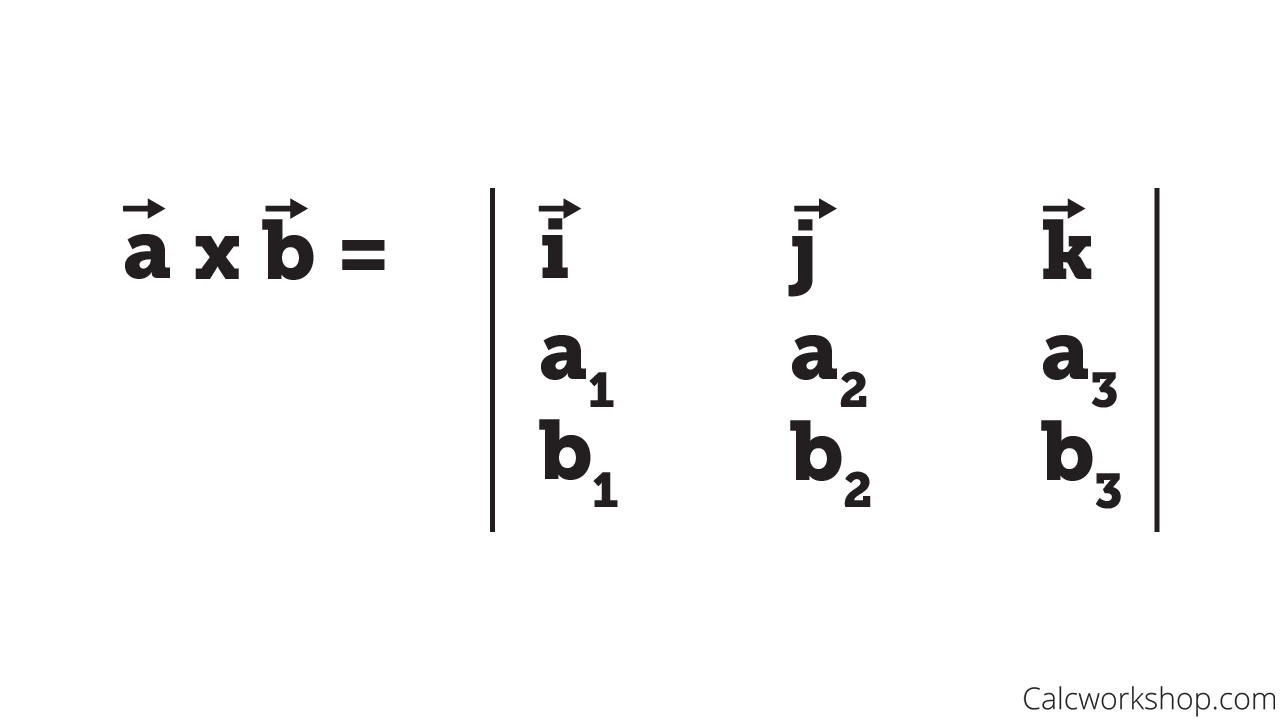
Geometric Meaning
The direction of cross product can be explained by the right hand rule. For example, i ⃗ × j ⃗ = k ⃗ \vec i \times \vec j = \vec k i×j=k.
∣ a ⃗ × b ⃗ ∣ |\vec a \times \vec b| ∣a×b∣ is the area of the above parallelogram.
∣ a ⃗ × b ⃗ ∣ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ s i n θ |\vec a \times \vec b| = |\vec a||\vec b| sin \theta ∣a×b∣=∣a∣∣b∣sinθ
Two non-zero vectors are parallel if their cross product is 0.
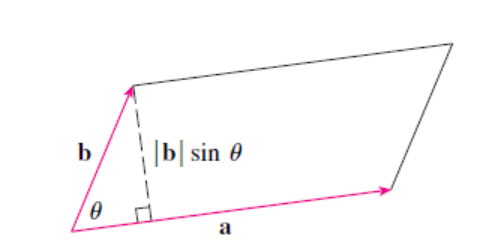
Properties
u ⃗ × v ⃗ = − v ⃗ × u ⃗ ( c u ⃗ ) × v ⃗ = c ( u ⃗ × v ⃗ ) u ⃗ × ( v ⃗ + w ⃗ ) = u ⃗ × v ⃗ + u ⃗ × w ⃗ \vec u \times \vec v = -\vec v \times \vec u \\\\ (c \vec u)\times \vec v = c(\vec u \times \vec v) \\\\ \vec u \times (\vec v + \vec w) = \vec u \times \vec v + \vec u \times \vec w\\\\ u×v=−v×u(cu)×v=c(u×v)u×(v+w)=u×v+u×w
Notice that, $\vec u \times (\vec v \times \vec w) \ne (\vec u \times \vec v) \times \vec w\\$.
Triple product
Claim: The volume of the parallelepiped determined by these three vectors is given by
V = ∣ a ⃗ ⋅ ( b ⃗ × c ⃗ ) ∣ V = |\vec a \cdot (\vec b \times \vec c)| V=∣a⋅(b×c)∣
Torque
The torque τ ⃗ \vec \tau τ is defined to be the cross product of F ⃗ \vec F F with r ⃗ \vec r r.
Reference
- Multivariable_Calculus_8th_Edition (12.1-12.4), James Stewart