第一章 多元正态分布
文章目录
§1.1 多元分布的基本概念
§1.1.1 随机向量
| 样品 \ 变量 |
X1 |
X2 |
… |
XP |
| 1 2 n |
x11 x21 xn1 |
x21 x22 xn2 |
… … … |
xP1 xP2 xPn |
如图数据是同时观测 p个指标（即变量），又进行了 n次观测得到的
则样本矩阵可用矩阵语言表示为:
若无特别说明，所称向量均指列向量
并且把这p个指标表示为
常用向量组成的
称为随机向量。
§1.1.2 分布函数与密度函数
联合分布函数：
设X=（X1,X2,⋯,Xp)'是一个 p维随机向量，定义 p 元函数
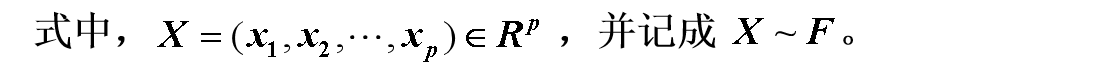
联合密度函数：
如果存在一个p元非负函数F(X)=f(x1,x2,x3,⋯,xp),使得对一切(x1,x2,x3,⋯,xp)都有
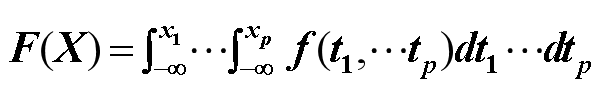
则称 f (x1,x2,⋯,xp) 为X的联合密度函数。
边际密度函数：
设 
为 r 维随机向量，
为 p−r随维机向量，且 和都是随机向量X的部分分量，满足
定义 的边际密度函数为
定义 的边际密度函数为
条件密度函数：
当 X 的密度函数可以写为 f (,) 时，定义给定 时的条件密度函数为
分量的独立性：
设 X1,X2,⋯ ,Xp是p个随机变量，则 X1,X2,⋯ ,Xp相互独立当且仅当
若 X = (X1,X2,⋯ ,Xp)' 的联合密度函数及其各个分量的密度函数均存在，则 X1,X2,⋯ ,Xp相互独立当且仅当
§1.1.3 随机向量的数字特征
1.随机向量的均值
设
有 p个分量。若
存在，
定义随机向量 的均值为
是一个p维向量，称为均值向量.
当A,B,C为常数矩阵时，由定义可立即推出如下性质：
2、随机向量 的协方差阵
称它为P维随机向量X的协方差阵，简称为X的协方差阵。称
为X的广义方差，它是协差阵的行列式之值。
3、随机向量X 和Y 的协差阵
设 
分别为p维和q维随机向量，它们之间的协方差阵定义为一个p*q矩阵，其元素是
，即
例题：
证明 ： 因为 X'AX不能直接求，所以需要如下
将X-u看作一个整体，将u看作一个整体，并进行计算
将上式乘出来得：
然后再对上式进行求期望
因为(X-u)'是1*p矩阵，A是p*p的常数矩阵，u是p*1均值向量矩阵，所以可以将Au看成一个整体=常数，再通过期望的性质E(ax) = aE(x)可知:aE(X-u)=a[E(x)-E(u)]=a(E(x)-u)=0，所以
所以等于求解
然后分开求前半部分为：
因为
的期望 = 它的迹
所以
又因为迹的性质：tr(AB) = tr(BA)
所以
又因为期望的迹 = 迹的期望
所以
又因为常数矩阵A的期望就是它本身，
所以
而
所以
综上，结果证得
4、随机向量X 的相关阵
若随机向量
的协差阵存在,且每个分量的方差大于零，则X的相关阵定义为:
5.标准化
在数据处理时，为了克服由于指标的量纲不同对统计分析结果带来的影响，往往在使用某种统计分析方法之前，常需将每个指标“标准化”，即做如下变换
