1 多层感知机&前馈神经网络&全连接网络
1.1 概述
1)前馈神经网络 (feedforward neural network),又称作深度前馈网络(deep feedforward network)、多层感知机(multilayer perceptron,MLP)
顾名思义,该网络中没有反向传播反馈,因此无法自动修改网络参数。
2)全连接网络 (Full connection)
在该网络中,除输入层外,每个节点都和上一层的所有节点两两相连。
2 前向传播
2.1 神经元模型
神经元模型示意图如下:

其中, x i x_i xi表示输入, w i w_i wi表示权重, z z z表示输入和, f f f表示激活函数, a a a表示神经元输出。
由上图可以得出神经元模型的完整表达式:
z = ∑ i = 1 n w i x i a = f ( w T x + b ) z=\sum_{i=1}^{n}w_{i}x_{i}\\ a=f(\mathbf{w}^{T}\mathbf{x} + b) z=i=1∑nwixia=f(wTx+b)
其中 f ( ) f() f()表示激活函数, w \mathbf{w} w表示权重是一个列向量, x \mathbf{x} x表示输入是一个列向量, b b b表示偏置。
2.2 多层感知机(MLP)
如图所示,将多个神经元并列即可形成一层神经神经网络,将多层神经元按顺序排好,就可以组成一个具有多层的神经网络。
其中从左到右,依次为输入层(input layer)、隐藏层(hidden layer)、输出层(output layer)。其中隐藏层可以有多层,而输入层和输出层只能有一层。
在整个神经网络中,信号从左向右按层传输。每一层中的神经元没有信号传输,相邻层之间的神经元两两连接。

2.3 前向传播(Forward Propagation)
从MLP模型取其中的两个隐藏层:
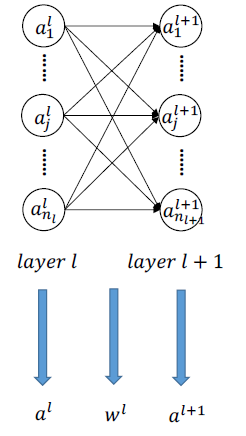
其中, l l l层的输出为 a l a^{l} al, l + 1 l+1 l+1层的输出为 a l + 1 a^{l+1} al+1,两层之间神经元两两相连,且权重为 w l w^{l} wl。
对于 l + 1 l+1 l+1层中的一个神经元,其连接情况如图所示:
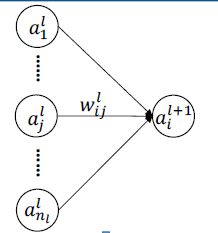
从图中可知, l l l层的神经元需要把信号传输给 l + 1 l+1 l+1层的神经元。
从中可以得出前向传播表达式:
z i l + 1 = ∑ j = 1 n w i j l a j l a i l + 1 = f ( z i l + 1 ) z_i^{l+1}=\sum_{j=1}^{n}w_{ij}^{l}a_{j}^{l}\\ a_{i}^{l+1}=f(z^{l+1}_i) zil+1=j=1∑nwijlajlail+1=f(zil+1)
其中, w i j l w_{ij}^{l} wijl 表示第 l l l 层中第 j j j 个神经元与第 l + 1 l+1 l+1 层中第 i i i 个神经元之间连接的权重 w w w 。
3 反向传播算法(Backpropagation)
3.1 全连接网络中的反向传播
反向传播中传播的是就是梯度。
在神经网络中,将输出层的结果与label作对比,可以求出loss,然后用loss对权重 w w w 和偏置 b b b 可以求出权重 w w w 和偏置 b b b 的梯度,然后根据梯度下降算法就可以改变 w w w 和 b b b 的值。
然后根据链式法则,将梯度依次传回上一层,从而修改上一层的权重 w w w 和偏置 b b b ,如此反复直到输入层,至此即可完成一轮的参数更新。
设:
- 损失函数 L ( w , b ) L(w, b) L(w,b)
- 神经元节点值 z i l + 1 = ∑ j = 1 n w i j l a j l z_i^{l+1}=\sum_{j=1}^{n}w_{ij}^{l}a_{j}^{l} zil+1=∑j=1nwijlajl
- 残差 δ i l = ∂ L ( w , b ) ∂ z i l \delta_i^l=\frac{\partial{L(w,b)}}{\partial{z_i^l}} δil=∂zil∂L(w,b)
所以损失函数对权重的偏导数与残差的关系如下:
∂ L ( w , b ) ∂ w i j l = ∂ L ( w , b ) ∂ z i l + 1 ∂ z i l + 1 ∂ w i j l = δ i l + 1 a j l \frac{\partial{L(w, b)}}{\partial{w_{ij}^l}}=\frac{\partial{L(w, b)}}{\partial{z_i^{l+1}}}\frac{\partial{z_i^{l+1}}}{\partial{w_{ij}^l}}=\delta_i^{l+1}a_j^{l} ∂wijl∂L(w,b)=∂zil+1∂L(w,b)∂wijl∂zil+1=δil+1ajl
同理可得损失函数对偏置的偏导数与残差的关系如下:
∂ L ( w , b ) ∂ b i l = ∂ L ( w , b ) ∂ z i l + 1 ∂ z i l + 1 ∂ b i l = δ i l + 1 \frac{\partial{L(w, b)}}{\partial{b_{i}^l}}=\frac{\partial{L(w, b)}}{\partial{z_i^{l+1}}}\frac{\partial{z_i^{l+1}}}{\partial{b_{i}^l}}=\delta_i^{l+1} ∂bil∂L(w,b)=∂zil+1∂L(w,b)∂bil∂zil+1=δil+1
然后再根据前向传播的方式可以推导出残差之间的关系如下:
δ i l = ∂ J ∂ z i l = ∑ j = 1 n l + 1 ∂ J ∂ z j l + 1 ⋅ ∂ z j l + 1 ∂ z i l = ∑ j = 1 n l + 1 δ j l + 1 ⋅ ∂ z j l + 1 ∂ z i l = ∑ j = 1 n l + 1 δ j l + 1 ⋅ w i j l f ˙ ( z i l ) = f ˙ ( z i l ) ⋅ ( ∑ j = 1 n l + 1 δ j l + 1 ⋅ w j i l ) \delta_{i}^{l}=\frac{\partial J}{\partial z_{i}^{l}}\\=\sum_{j=1}^{n_{l+1}} \frac{\partial J}{\partial z_{j}^{l+1}} \cdot \frac{\partial z_{j}^{l+1}}{\partial z_{i}^{l}}\\=\sum_{j=1}^{n_{l+1}} \delta_{j}^{l+1} \cdot \frac{\partial z_{j}^{l+1}}{\partial z_{i}^{l}}\\=\sum_{j=1}^{n_{l+1}} \delta_{j}^{l+1} \cdot w_{ij}^{l} \dot{f}\left(z_{i}^{l}\right)\\=\dot{f}\left(z_{i}^{l}\right) \cdot\left(\sum_{j=1}^{n_{l+1}} \delta_{j}^{l+1} \cdot w_{j i}^{l}\right) δil=∂zil∂J=j=1∑nl+1∂zjl+1∂J⋅∂zil∂zjl+1=j=1∑nl+1δjl+1⋅∂zil∂zjl+1=j=1∑nl+1δjl+1⋅wijlf˙(zil)=f˙(zil)⋅(j=1∑nl+1δjl+1⋅wjil)
有了残差的传递关系之后,我们就可以求出每层 w w w 和 b b b 的梯度,从而更新每一层的 w w w 和 b b b。
w i j l = w i j l − η a i l δ j l + 1 w_{ij}^{l} = w_{ij}^{l} - \eta a_i^l \delta_j^{l+1} wijl=wijl−ηailδjl+1
b i l = b i l − η δ j l + 1 b_{i}^l=b_i^l-\eta \delta_j^{l+1} bil=bil−ηδjl+1
未完待续。。。