D. The Number of Pairs (裴蜀定理、埃式筛)

题目

思路：对于c⋅lcm(a,b)−d⋅gcd(a,b)=x，由裴蜀定理可得想要使该式c,d为整数成立则x=k * gcd(gcd(a,b),lcm(a,b))=ngcd，所以第一个条件得出gcd的是x的因数。且c,d,x都已经明确给出，我们枚举每个x的因数作为gcd时会得出对应的lcm=(dgcd+x)/c，如果lcm不为整数排除。

那么现在我们已经花费O(n^(1/2))求出了每个gcd作为x的因子，现在要求的就是每一步中知道了gcd(a,b),lcm(a,b)求出相应的a,b有多少种可能。

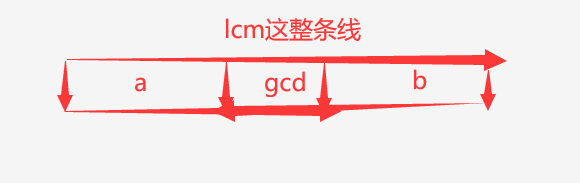a,b,gcd,lcm关系差不多如上图，将lcm/gcd=(a/gcd) * (b/gcd)，lcm/gcd会得到a/gcd(属于a除以公共gcd的值) * b/gcd(b除以公共gcd的值)，将lcm/gcd质因数分解，其中每个质因数只能单独属于a或者b（如果a有这个因数，b也有这个因数,这个因数就属于到gcd里面了），现在我们求出了lcm/gcd有多少种质因数，每种质因数有两个选择属于a或b，所贡献为pow(2,lcm/gcd所含的质因子种数)，用埃拉托色尼筛法提前求出每个数所含的质因数种数即可。

Code:

#include<iostream>
#include<cmath>
#include<map>
typedef long long ll;
using namespace std;
const int Max = 2e7+5;
int su[Max];

void era()
{
    
    
	for (int i = 2;i <= Max;i++)
	{
    
    
		if (su[i] == 0)
		{
    
    
			int j = 1;
			while (j * i <= Max)
			{
    
    
				su[i*j]++;
				j++;
			}
		}
	}
}

int main()
{
    
    
	era();
	int t;cin >> t;
	while (t--)
	{
    
    
		ll c, d, x;cin >> c >> d >> x;
		ll ans = 0;
		for (int i = 1;i * i <= x;i++)
		{
    
    
			if (x % i != 0)continue;
			ll lcm = x + d * i;
			if (lcm % c == 0)
			{
    
    
				lcm /= c;
				if (lcm % i == 0)
				{
    
    
					ans += ll(1) << su[lcm / i];
				}
			}
			if (i * i == x)continue;
			lcm = x + d * (x / i);
			if (lcm % c == 0)
			{
    
    
				lcm /= c;
				if (lcm % (x / i) == 0)
				{
    
    
					ans += ll(1) << su[lcm / (x / i)];
				}
			}
		}
		cout << ans << endl;
	}
}