ICPC基础数学知识点整理

都没怎么学过数学呜呜呜呜，太菜了记录一下碰到的各种数学相关的基础知识点吧。

然后其中的ppt部分来自于牛客邓丝雨学姐的算法入门课

数论

质数和质数筛

N>3时，任意的N 和 N+1 必有一个不是质数。

N和N+2都为质数，这样的一对质数被称为孪生质数。如3和5,5和7，1e9+1和1e9+9

素数筛：
其他的筛法都比较熟了，就只列一个线性筛：

int pri[N+9>>1],now;
bool vis[N+9];
void init(){
    
    
    for(int i=2;i<=N;i++){
    
    
        if(!vis[i])pri[++now]=i;
        for(int j=1;j<=now&&pri[j]*i<=N;j++){
    
    
            vis[pri[j]*i]=1;
            if(i%pri[j]==0)break;
        }
    }
}

gcd

求最大公因数的递归写法辗转相除法

ll gcd(ll a, ll b){
    
    
    if(b == 0) return a;
    else return gcd(b, a%b);
}

最小公倍数$lcm=a/gcd(a,b)\ast b$

还有几个公式
$gcd(ka,kb)=k\ast gcd(a,b)$
$lcm(ka,kb)=k\ast lcm(a,b)$
$lcm(\frac{S}{a},\frac{S}{b})=\frac{S}{gcd(a,b)}$

扩展gcd

贝祖定理：即如果a、b是整数，那么一定存在整数x、y使得ax+by=gcd(a,b)。

换句话说，如果ax+by=m有解，那么m一定是gcd(a,b)的若干倍。（可以来判断一个这样的式子有没有解）

有一个直接的应用就是 如果ax+by=1有解，那么gcd(a,b)=1

int exgcd(int a,int b,int &x,int &y)//扩展欧几里得算法
{
    
    
    if(!b)
    {
    
    
        x=1;y=0;
        return a;  //到达递归边界开始向上一层返回
    }
    int r=exgcd(b,a%b,x,y);
    int temp=y;    //把x y变成上一层的
    y=x-(a/b)*y;
    x=temp;
    return r;     //得到a b的最大公因数
}

欧拉函数

欧拉函数是求小于等于n的数中与n互质的数的数目

2020年省赛出过的点，当时就是没学过欧拉函数卡在这儿了
计算公式：
欧拉函数是一个积性函数:$\varphi (a\times b)=\varphi (a)\times \varphi (b)$

首先上证明(参考博客：https://www.cnblogs.com/linyujun/p/5194170.html)
随便这个大佬的博客tql，建议反复看

证明过程需要引入一个唯一分解定理：

唯一分解定理：

（2020的蓝桥杯国赛的一个填空题出过，我不知道当时我怎么就忘了，太菜了）

唯一分解定理又称为算数基本定理，基本内容是：

每个大于1的自然数，要么本身就是质数，要么可以写为2个或以上的质数的积，而且这些质因子按大小排列之后，写法仅有一种方式。

用另一种方法表示就是：对于任何一个大于1的正整数,都存在一个标准的分解式: $N=p_1^{a_1}\ast {p_2}^{a_2}\ast \cdot \cdot \cdot \ast p_n^{a_n}$（其中一系列$a_n$为指数，$p_n$为质数）

此定理表明：任何一个大于 1 的正整数都可以表示为素数的积。

通过唯一分解定理，可以先求出一个数x的质因数，然后删掉所有小于x的质因数的倍数的个数，重复减去的又要加上（容斥嘛），然后用一种简单写法写容斥就可以了。

欧拉函数的代码（其中包括了怎么分解质因数）：

int phi(int x){
    
    
    int ans = x;
    for(int i = 2; i*i <= x; i++){
    
    
        if(x % i == 0){
    
    
            ans = ans / i * (i-1);
            while(x % i == 0) x /= i;//分解质因数
        }
    }
    if(x > 1) ans = ans / x * (x-1);//除剩下的那个数如果不是1也是质因数
    return ans;
}

另外唯一分解定理还有推论：

欧拉定理

如果正整数n和a互质,那么就有$a^{\varphi (n)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}n)$,其中$\varphi (n)$是欧拉函数

推论：欧拉降幂

当指数很大时，可以用欧拉定理降幂：

如果n和a互质，那么$a^b\equiv a^{b\mathrm{m}\mathrm{o}\mathrm{d}\varphi (n)}(\mathrm{m}\mathrm{o}\mathrm{d}n)$

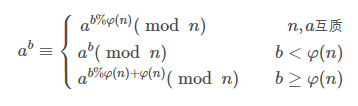
费马小定理

或者说，若p是质数，且a,p互质，那么 a的(p-1)次方除以p的余数恒等于1。

可以用来求逆元，另外欧拉定理是费马小定理的推广。

在有取模的情况下，除法需要特殊处理，也就是逆元，将除法变为乘法。（关于逆元https://blog.csdn.net/u011815404/article/details/81298032可以看这个大佬的博客）

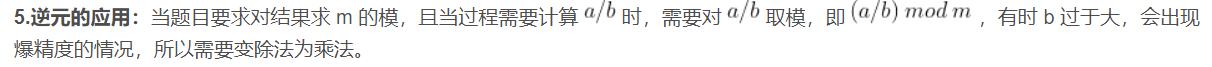
中国剩余定理

中国剩余定理用于求解一元线性同余方程组

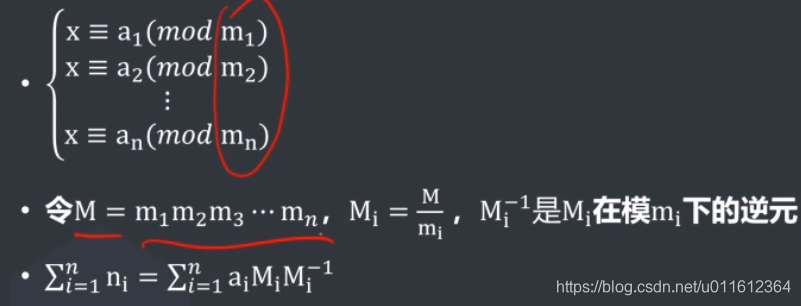
比如说：一堆物品，3个3个分剩2个，5个5个分剩3个，7个7个分剩2个。

用inv(x,y)表示x在模y下的逆元

用中国剩余定理其实就相当于构造$2\times (5\times 7\times inv(5\times 7,3))$，$3\times (3\times 7\times inv(3\times 7,5))$，$2\times (3\times 5\times inv(3\times 5,7))$，最终的答案是这三个数的和。

代码：

//中国剩余定理模板
typedef long long ll;
ll china(ll a[],ll b[],int n)//a[]为除数，b[]为余数
{
    
    
    ll M=1,y,x=0;
    for(int i=0;i<n;++i)  //算出它们累乘的结果
        M*=a[i];
    for(int i=0;i<n;++i)
    {
    
    
        ll w=M/a[i];
        ll tx=0;
        int t=exgcd(w,a[i],tx,y);  //计算逆元
        x=(x+w*(b[i]/t)*x)%M; 
    }
    return (x+M)%M;
}

组合数学

组合公式：$C_n^m=\frac{n!}{m!(n-m)!}$

基本性质：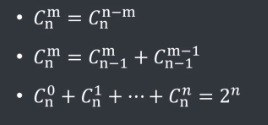

递推关系：$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$（可以用杨辉三角辅助记忆）

（背住，求组合数小的时候用这个公式递推，大了就用卢卡斯)

一般来说，求组合数$C_n^m$时，n<1000,用递推公式；n<1e5,用逆元；n<1e18,且p为质数，用lucas。

逆元求

你直接算出来一个组合数的结果直接对p取模，结果一定是对的，但是n大了之后答案存不下太大了，所以需要取模。

逆元求就是我们现实中的公式法，不同的是变除法为乘除数的逆元。

求逆元的两种方法：

1、费马小定理（有限制，p要为素数）
p为素数时，a关于mod p的逆元为a^(p-2)mod p。用快速幂模。
但是实际上在acm中题目给的p基本都是质数，所以这是最好用的啦。

2、扩展欧几里得（普遍使用的求逆元方法）

例题：组合数问题https://ac.nowcoder.com/acm/contest/9986/F
对应题解可以看我这篇博客F题

lucas定理（大组合数）

Lucas定理是用来求 $C_n^m$mod p，p为素数的值。（p最大1e5左右）。

是由递推式得到的。

这个可以参考我的博客中：B题
代码：

ll lucas(ll n,ll m){
    
    
    if(m==0)
        return 1;
    return (C(n%p,m%p)*lucas(n/p,m/p))%p;
}

二项式定理

鸽巢原理

容斥原理

奇数个集合相加，偶数个集合相减