[机器学习] - 支持向量机（三）： 序列最小优化算法(SMO算法)

本文是翻译：斯坦福的cs229机器学习SVM课程PDF（SMO部分）
原文链接：chrome-extension://ibllepbpahcoppkjjllbabhnigcbffpi/http://cs229.stanford.edu/notes2019fall/cs229-notes3.pdf

---

1 cs229课程（SMO部分）翻译：

接下来，我们来简单推导一下 SMO 算法，作为 SVM（支持向量机算法）相关讨论的收尾。一些具体的细节就省略掉了，放到作业里面了，其他的一些内容可以参考课堂上发的纸质材料。

下面就是一个（对偶）优化问题：

$$\begin{array}{rlr}\underset{\alpha }{\max }& W(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{y}^{(i)}{y}^{(j)}{\alpha }_i{\alpha }_j⟨x^{(i)},x^{(j)}⟩& \text{(17)}\end{array}$$

$$\begin{array}{rlr}s.t.& 0\le {\alpha }_i\le C,i=1,...,m& \text{(18)}\end{array}$$

$$\begin{array}{rlr}& \sum _{i=1}^m{\alpha }_i{y}^{(i)}=0& \text{(19)}\end{array}$$

我们假设有一系列满足约束条件 $(18-19)$ 的 ${\alpha }_i$ 构成的集合。接下来，假设我们要保存固定的 ${\alpha }_2,...,{\alpha }_m$ 的值，然后进行一步坐标上升，重新优化对应 ${\alpha }_1$的目标值(re-optimize the objective with respect to ${\alpha }_1$)。这样能解出来么？很不幸，不能，因为约束条件 $(19)$ 就意味着：

$${\alpha }_1{y}^{(1)}=-\sum _{i=2}^m{\alpha }_i{y}^{(i)}$$

或者，也可以对等号两侧同时乘以 $y^{(1)}$ ，然后会得到下面的等式，与上面的等式是等价的：

$${\alpha }_1=-y^{(1)}\sum _{i=2}^m{\alpha }_i{y}^{(i)}$$

（这一步用到了一个定理，即 $y^{(1)}\in -1,1$，所以$(y^{(1)}{)}^2=1$）可见 ${\alpha }_1$ 是由其他的 ${\alpha }_i$ 决定的，这样如果我们保存固定的 ${\alpha }_2,...,{\alpha }_m$ 的值，那就根本没办法对 ${\alpha }_1$ 的值进行任何修改了，否则不能满足优化问题中的约束条件 $(19)$ 了。

所以，如果我们要对 ${\alpha }_i$ 当中的一些值进行更新的话，就必须至少同时更新两个，这样才能保证满足约束条件。基于这个情况就衍生出了 SMO 算法，简单来说内容如下所示：

重复直到收敛 {

1. 选择某一对的 ${\alpha }_i$ 和 ${\alpha }_j$ 以在下次迭代中进行更新 (这里需要选择那种能朝全局最大值方向最大程度靠近的一对值)。
2. 使用对应的 ${\alpha }_i$ 和 ${\alpha }_j$ 来重新优化(Re-optimize) $W(\alpha )$ ，而保持其他的 ${\alpha }_k$ 值固定($k\ne i,j$)。
   }

我们可以检查在某些收敛公差参数 tol 范围内，KKT 对偶互补条件能否被满足，以此来检验这个算法的收敛性。这里的 tol 是收敛公差参数(convergence tolerance parameter)，通常都是设定到大概 $0.01$ 到 $0.001$。（更多细节内容参考文献以及伪代码。）

SMO 算法有效的一个关键原因是对 ${\alpha }_i,{\alpha }_j$ 的更新计算起来很有效率。接下来咱们简要介绍一下推导高效率更新的大概思路。

假设我们现在有某些 ${\alpha }_i$ 满足约束条件 $(18-19)$，如果我们决定要保存固定的 ${\alpha }_3,...,{\alpha }_m$ 值，然后要使用这组 ${\alpha }_1$ 和 ${\alpha }_2$ 来重新优化 $W({\alpha }_1,{\alpha }_2,...,{\alpha }_m)$ ，这样成对更新也是为了满足约束条件。根据约束条件 $(19)$，可以得到：

$${\alpha }_1{y}^{(1)}+{\alpha }_2{y}^{(2)}=-\sum _{i=3}^m{\alpha }_i{y}^{(i)}$$

等号右边的值是固定的，因为我们已经固定了${\alpha }_3,...,{\alpha }_m$ 的值，所以就可以把等号右边的项目简写成一个常数 $\zeta$:

$${\alpha }_1{y}^{(1)}+{\alpha }_2{y}^{(2)}=\zeta \text{(20)}$$

然后我们就可以用下面的图来表述对 ${\alpha }_1$ 和 ${\alpha }_2$ 的约束条件：

　　根据约束条件$(18)$，可知 必须在图中 ${\alpha }_1$和 ${\alpha }_2$ 必须在 $[0,C]\times [0,C]$ 所构成的方框中。另外图中还有一条线 ${\alpha }_1{y}^{(1)}+{\alpha }_2{y}^{(2)}=\zeta$，而我们知道${\alpha }_1$和 ${\alpha }_2$ 必须在这条线上。还需要注意的是，通过上面的约束条件，还能知道 $L\le {\alpha }_2\le H$；否则 (${\alpha }_1,{\alpha }_2$) 就不能同时满足在方框内并位于直线上这两个约束条件。在上面这个例子中，$L=0$。但考虑到直线 ${\alpha }_1{y}^{(1)}+{\alpha }_2{y}^{(2)}=\zeta$ 的形状方向，这个 $L=0$ 还未必就是最佳的；不过通常来讲，保证${\alpha }_1,{\alpha }_2$ 位于 $[0,C]\times [0,C]$ 方框内的 ${\alpha }_2$ 可能的值，都会有一个下界 $L$ 和一个上界 $H$。

利用等式$(20)$，我们还可以把 ${\alpha }_1$ 写成 ${\alpha }_2$ 的函数的形式：

$${\alpha }_1=(\zeta -{\alpha }_2{y}^{(2)})y^{(1)}$$

（自己检查一下这个推导过程吧；这里还是用到了定理：$y^{(1)}\in -1,1$，所以 $(y^{(1)}{)}^2=1$。）所以目标函数 $W(\alpha )$ 就可以写成：
$$W({\alpha }_1,{\alpha }_2,...,{\alpha }_m)=W((\zeta -{\alpha }_2{y}^{(2)})y^{(1),{\alpha }_2,...,{\alpha }_m})$$

把 ${\alpha }_3,...,{\alpha }_m$ 当做常量，你就能证明上面这个函数其实只是一个关于 ${\alpha }_2$ 的二次函数。也就是说，其实也可以写成 $a{\alpha }_2^2+b{\alpha }_2+c$ 的形式，其中的 $a,b,c$ 参数。如果我们暂时忽略掉方框约束条件(18)(也就是说 $L\le {\alpha }_2\le H)$，那就很容易通过使导数为零来找出此二次函数的最大值，继而进行求解。我们设 ${\alpha }_2^{new,unclipped}$ 表示为 $\alpha$ 的结果值。你需要自己证明，如果我们要使关于 ${\alpha }_2$ 的函数 $W$取最大值，而又受到方框约束条件的限制，那么就可以把 ${\alpha }_2^{new,unclipped}$的值“粘贴”到$[L,H]$ 这个间隔内，这样来找到最优值结果，就得到了：

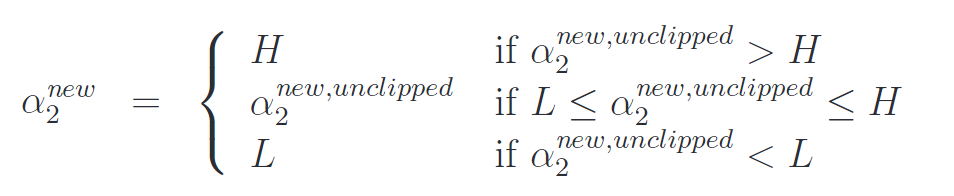
　　最终，找到了 ${\alpha }_2^{new}$ 之后，就可以利用等式$(20)$来代回这个结果，就能得到 ${\alpha }_1^{new}$ 的最优值。
　　此外还有一些其他的细节，也都挺简单，不过这里就不讲了，你自己去读一下 Platt 的论文吧：一个是用于对后续用于更新的 ${\alpha }_i,{\alpha }_j$ 启发式选择; 另一个是如何在 SMO算法 运行的同时来对 $b$ 进行更新。

2 SMO算法步骤

3 总结

（1） ${\alpha }_1$和 ${\alpha }_2$的选择。

1. 第1个变量${\alpha }_1$的选择要尽量选择违背KKT条件最严重的点。我的理解是，先遍历所有满足$0<a_i<C$的样本点，也就是间隔上的支持向量点，然后判断是否满足$y_{i}g(x_i)=1$，可能正的支持向量点在负的分割线上，此时$y_{i}g(x_i)=-1$。找到不能满足KKT条件的支持向量。$g(x)=w^{\ast }\cdot \varphi (x)+b=\sum _{j=1}^m{\alpha }_j^{\ast }{y}_{j}K\left(x,x_j\right)+b^{\ast }$。
2. 在选择${\alpha }_2$时，要确定$E_1$，$E_1$是函数$g(x)$对结点$x_1$的预测值与真实的输入值$y_1$之差$E_1=g(x_1)-y_1$。我们的目标是使其$|E_1-E_2|$最大，因${\alpha }_1$已定，$E_1$也确定了，如果$E_1$为正，则在样本点中找到最小的$E_i$作为$E_2$，如果$E_1$为负，则在样本点中找到最大的$E_i$作为$E_2$，进而确定了${\alpha }_2$。

（3）SMO算法是支持向量机学习的一种快速算法， 其特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题，并对子问题进行解析求解，直到所有变量满足KKT条件为止。这样通过启发式的方法得到原二次规划问题的最优解。因为子问题有解析解，所以每次计算子问题都很快，虽然计算子问题次数很多，但在总体上还是高效的。

参考资料：
1 https://www.cnblogs.com/pinard/p/6111471.html
2 chrome-extension://ibllepbpahcoppkjjllbabhnigcbffpi/http://cs229.stanford.edu/notes2019fall/cs229-notes3.pdf
3 李航《统计学习方法》