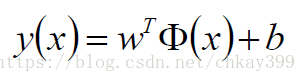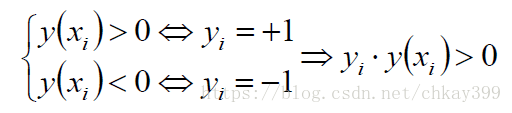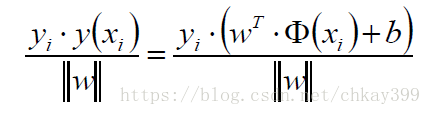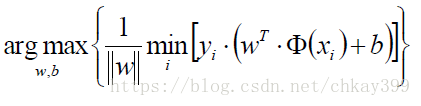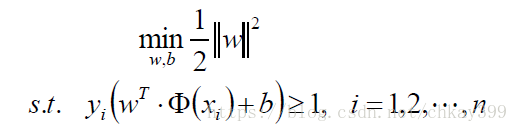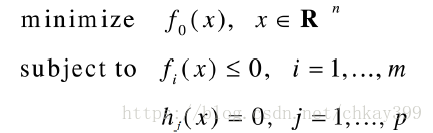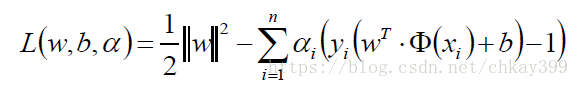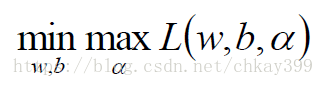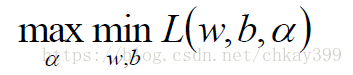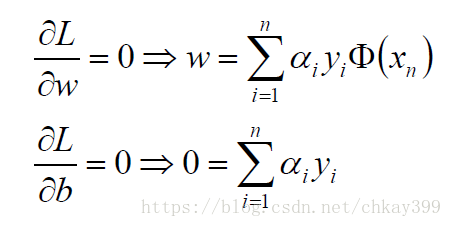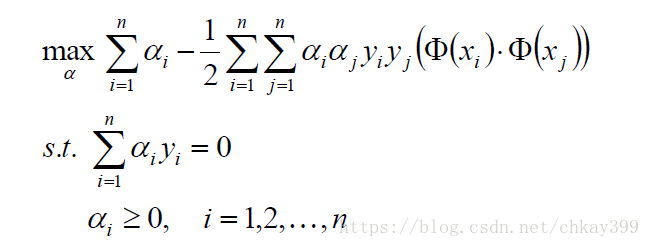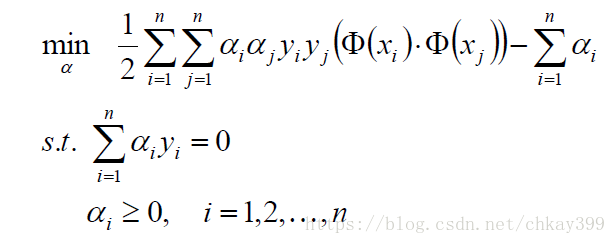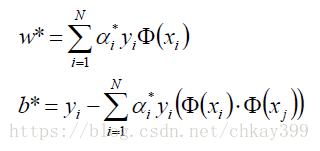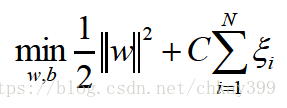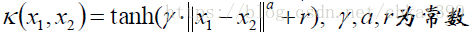支持向量机(SVM,support vectors machine)的算法原理比较简单,就是寻找最大间隔讲两个类别分开,从数学上推可能复杂点。按照样本的情况一下三种:
①当训练样本线性可分时,通过硬间隔最大化——线性可分支持向量机;
②当训练样本近似线性可分时,通过软间隔最大化——线性支持向量机;
③当训练样本线性不可分时,通过核技巧和软间隔最大化——非线性支持向量机;
首先从线性可分支持向量机开始推导,要找到讲两个样本分隔开的超平面,且使两边到超平面距离最近的点到超平面距离之和最大。这个超平面表示为:
那我们就可以通过sign(y(x))来预测一个样本时属于正类还是负类。我们将分为正类的yi设为+1,负类为-1,即yi∈{+1,-1},对于超平面上下的点有:
点到超平面的距离为:
总可以缩放w的方式将分子的最小项(即离超平面最近的点)等于1,即令|y|≥1。这样原来的目标函数为
就变成了新的目标函数:
因为我们主要是想求得该目标函数时对应的w和b值,随意可以对目标函数稍作变化,原来的求解问题:
变为求最小值
接下来要做的就是利用拉格朗日乘子法来求解这个问题了。一般优化问题的拉格朗日乘子法具体如下:
那原来的问题对应的拉格朗日函数为:
这里需要对目前的问题转换为其对偶问题,原问题是极小极大值问题(对于对偶问题,这个网址介绍的比较清楚,可以参见http://www.hanlongfei.com/convex/2015/11/05/duality/):
其对偶问题是极大极小值问题:
拉格朗日函数L(w, b, α)对w、b求导得到:
回代到原拉格朗日函数L(w, b, α)得到:
整理得到:
这个问题解得最优解,代入下式计算:
进而可以得到超平面:
得到分类决策函数:
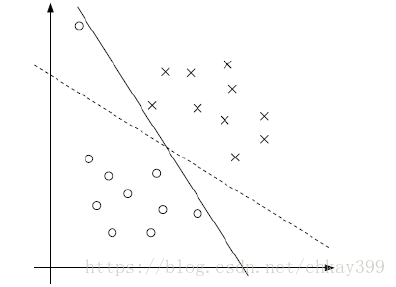
对于线性支持向量机,是针对不一定分类完全正确的超平面就是最好的(主要是靠近超平面的点可能标记错误等),以及样本数据点本身不可以线性可分(比如边界附近两类点相互混杂)的情况,如下图:
我们要做的就是在约束条件中加入约束因子ξ:
目标函数变成了
其中C值代表严格程度,C值越大越严格,越不允许分错(趋于无穷是即为前面的线性可分支持向量机了),C值越小,缓冲带越大,越包容中间可以分错的情况。目标函数求解的过程与前面相似,不再赘述了。
核函数是针对在原始的特征空间中样本线性不可分,因此使用核函数将原始特征空间映射到新的高维空间中,从而使样本可以在核空间中可分。常常使用的核函数有:
-多项式核函数
-高斯核函数,也叫做径向基函数(RBF,Radial Basis Function )
-Sigmoid核函数
但是将点映射到多维空间会是计算量极大的增加,但是我们发现K<x, y>=<Φ(x), Φ(y)>,也就是说在高维空间的计算其实等于核函数在低维空间的计算,这样便极大的降低了计算量。
核函数所反映的低维向高维的映射关系是不确定的,例如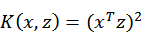 展开后为
展开后为
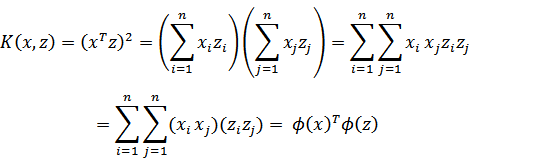
假如原始特征空间是2维的,则Φ(x)可以是将2维映射到4维如Φ(x)=(,
,
,
),也可以是3维如Φ(x)=(
,
,
)。高斯核函数是映射到无穷维特征空间的,推导如下:
其中Φ(x)的映射表达式为:
在实际应用中,往往依赖先验领域知识或者交叉验证等方法来确定有效的核函数,当没有更多先验知识时,一般使用高斯核函数。