[NOI2007] 货币兑换 （dp+李超树维护凸包）

description

小Y最近在一家金券交易所工作。该金券交易所只发行交易两种金券：A纪念券（以下简称A券）和 B纪念券（以下简称B券）。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动，两种金券都有自己当时的价值，即每一单位金券当天可以兑换的人民币数目。我们记录第 K 天中 A券 和 B券 的价值分别为 AK 和 BK（元/单位金券）。为了方便顾客，金券交易所提供了一种非常方便的交易方式：比例交易法。比例交易法分为两个方面：（a）卖出金券：顾客提供一个 [0,100] 内的实数 OP 作为卖出比例，其意义为：将 OP% 的 A券和 OP% 的 B券 以当时的价值兑换为人民币；（b）买入金券：顾客支付 IP 元人民币，交易所将会兑换给用户总价值为 IP 的金券，并且，满足提供给顾客的A券和B券的比例在第 K 天恰好为 RateK；例如，假定接
下来 3 天内的 Ak、Bk、RateK 的变化分别为：

假定在第一天时，用户手中有 100元 人民币但是没有任何金券。用户可以执行以下的操作：

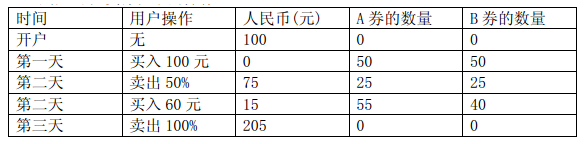
注意到，同一天内可以进行多次操作。小Y是一个很有经济头脑的员工，通过较长时间的运作和行情测算，他已经知道了未来N天内的A券和B券的价值以及Rate。他还希望能够计算出来，如果开始时拥有S元钱，那么N天后最多能够获得多少元钱。

Input
输入第一行两个正整数N、S，分别表示小Y能预知的天数以及初始时拥有的钱数。接下来N行，第K行三个实数AK、BK、RateK，意义如题目中所述
对于100%的测试数据，满足：0<AK≤10；0<BK≤10；0<RateK≤100；MaxProfit≤0^9。
【提示】
1.输入文件可能很大，请采用快速的读入方式。
2.必然存在一种最优的买卖方案满足：
每次买进操作使用完所有的人民币；
每次卖出操作卖出所有的金券。

Output
只有一个实数MaxProfit，表示第N天的操作结束时能够获得的最大的金钱数目
答案保留3位小数。

Sample Input
3 100
1 1 1
1 2 2
2 2 3
Sample Output
225.000
Hint

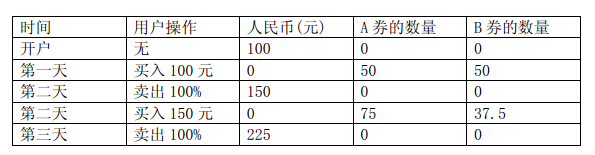
solution

乍一看跟以前做过的股票交易挺像的，这个式子长得就斜率优化诱惑

---

Step1
贪心。。。
在某一天要么买股票把钱买完，要么卖股票把股票卖完
不会有人赚钱只赚一半就跑了吧

---

Step2
考虑列出状态转移方程
设$f_i$表示$i$天能赚的最多的钱，$a_i$为$i$天最多能买的$A$股票数，$b_i$为$i$天最多能买的$B$股票数
①在$i$天买入股票$$a_i=\frac{f_i\times Rat{e}_i}{A_i\times Rat{e}_i+B_i},b_i=\frac{f_i}{A_i\times Rat{e}_i+B_i}$$
②在$i$天不买不卖
$$f_i=max(f_i,f_{i-1})$$
③在$i$天卖股票，枚举在$j$天买入的股票
f i = m a x { a j ∗ A i + b j ∗ B i } f_i=max\{a_j*A_i+b_j*B_i\} fi​=max{ aj​∗Ai​+bj​∗Bi​}
对式子进行变形
f i = m a x { B i × ( A i B i ∗ a j + b j ) } f_i=max\{B_i\times (\frac{A_i}{B_i}*a_j+b_j)\} fi​=max{ Bi​×(Bi​Ai​​∗aj​+bj​)}

---

Step3
李超线段树维护凸包
将$f_i$的式子看作直线$kx+b$
$k=a_j,x=\frac{A_i}{B_i},b=b_j$

code

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define maxn 100005
int n;
double ans;
double A[maxn], B[maxn], Rate[maxn], c[maxn], x[maxn], k[maxn], b[maxn];
int t[maxn << 2];

double calc( int i, int pos ) {
    
    
	return k[i] * x[pos] + b[i];
}

void modify( int num, int l, int r, int id ) {
    
    
	if( l == r ) {
    
    
		if( calc( id, l ) > calc( t[num], l ) ) t[num] = id;
		return;
	}
	int mid = ( l + r ) >> 1;
	if( calc( id, mid ) > calc( t[num], mid ) ) swap( t[num], id );
	if( calc( id, l ) > calc( t[num], l ) ) modify( num << 1, l, mid, id );
	if( calc( id, r ) > calc( t[num], r ) ) modify( num << 1 | 1, mid + 1, r, id );
}

double query( int num, int l, int r, int pos ) {
    
    
	if( l == r ) return calc( t[num], pos );
	int mid = ( l + r ) >> 1;
	if( pos <= mid ) return max( calc( t[num], pos ), query( num << 1, l, mid, pos ) );
	else return max( calc( t[num], pos ), query( num << 1 | 1, mid + 1, r, pos ) ); 
}

int main() {
    
    
	scanf( "%d %lf", &n, &ans );
	for( int i = 1;i <= n;i ++ ) {
    
    
		scanf( "%lf %lf %lf", &A[i], &B[i], &Rate[i] );
		x[i] = c[i] = A[i] / B[i];
	}
	sort( x + 1, x + n + 1 );
	for( int i = 1;i <= n;i ++ ) {
    
    
		int p = lower_bound( x + 1, x + n + 1, c[i] ) - x;
		ans = max( ans, B[i] * query( 1, 1, n, p ) );
		double g = A[i] * Rate[i] + B[i];
		k[i] = ans * Rate[i] / g, b[i] = ans / g;
		modify( 1, 1, n, i );
	}
	printf( "%.3f\n", ans );
	return 0;
}