多元线性回归
使用多个特征值实现对目标的预测。
多个特征值/变量
Notion:
n n n:特征数量
x ( i ) x^{(i)} x(i):第 i i i 个训练样本的输入特征值
x j ( i ) x^{(i)}_j xj(i):第 i i i 个训练样本的第 j j j 个特征值
example:
房子特征与房价
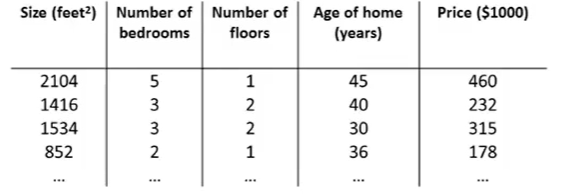
- x ( 2 ) = [ 1416 3 2 40 ] x^{(2)}= \left[ \begin{matrix} 1416 \\ 3 \\ 2 \\ 40 \end{matrix} \right] x(2)=⎣⎢⎢⎡14163240⎦⎥⎥⎤表示第2个房子的4个特征值
- x 3 ( 2 ) = 2 x^{(2)}_3 = 2 x3(2)=2 表示第2个房子的第3个特征值
假设函数
需要将 n n n 个特征量相加
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n hθ(x)=θ0+θ1x1+θ2x2+...+θnxn
为了方便,定义 x 0 = 1 x_0 = 1 x0=1
则,n+1维特征量向量 X = [ x 0 x 1 x 2 . . . x n ] X=\left[ \begin{matrix} x_0\\ x_1 \\ x_2 \\ ... \\ x_n \end{matrix} \right] X=⎣⎢⎢⎢⎢⎡x0x1x2...xn⎦⎥⎥⎥⎥⎤, θ = [ θ 0 θ 1 θ 2 . . . θ n ] \theta=\left[ \begin{matrix} \theta_0\\ \theta_1 \\ \theta_2 \\ ... \\ \theta_n \end{matrix} \right] θ=⎣⎢⎢⎢⎢⎡θ0θ1θ2...θn⎦⎥⎥⎥⎥⎤
则, h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n = θ T X h_\theta(x) = \theta_0x_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n = \theta^TX hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxn=θTX
多元梯度下降法
算法描述
Repeat {
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta) θj:=θj−α∂θj∂J(θ) (for j = 0 , . . . n j = 0,...n j=0,...n)
}
即
Repeat {
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) \theta_j:=\theta_j-\alpha\frac{1}{m} \sum\limits_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})·x^{(i)}_j θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))⋅xj(i) (for j = 0 , . . . n j = 0,...n j=0,...n)
}
特征缩放(feature scaling)
梯度下降算法中,在有多个特征的情况下,如果你能确保这些不同的特征都处在一个相近的范围,这样梯度下降法就能更快地收敛。
一般情况下,通常将每一个特征取值约束在 − 1 ≤ x i ≤ 1 -1≤x_i≤1 −1≤xi≤1

特征缩放并不需要太精确,其目的只是为了让梯度下降能够运行得更快一点,让梯度下降收敛所需的循环次数更少一些而已。
均值归一化(mean normalization)
除了在特征缩放中将特征除以最大值以外,有时候我们也会进行一个称为均值归一化(mean normalization)的工作。
替换 x i x_i xi 为 x i − μ i x_i-\mu_i xi−μi 使特征值具有为 0 0 0 的平均值(不需要应用到 x 0 = 1 x_0 = 1 x0=1 )
example:
x 1 = s i z e − s i z e ˉ m a x ( s i z e ) − m i n ( s i z e ) x_1 = \frac{size-\bar{size}}{max(size)-min(size)} x1=max(size)−min(size)size−sizeˉ
分母也可以为标准差
多元梯度下降迭代
正常情况下,每一次迭代后 J ( θ ) J(\theta) J(θ) 都应该下降。
另外,可以进行一些自动收敛测试,也就是说让一种算法来告诉你梯度下降算法是否已经收敛,比如,代价函数在一步迭代后的下降小于一个很小的值 ϵ \epsilon ϵ,那么就判定函数已经收敛
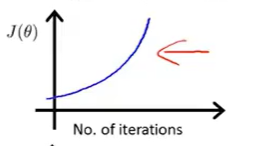
另一种情况,假如代价函数随着迭代步数变化曲线呈上升趋势(下图一),这就表明梯度下降算法没有正常工作,通常意味着应该使用较小的学习率 α \alpha α 。如果代价函数上升,最常见的的原因就是在尝试最小化以下这样的函数(下图二),由于学习率过大,导致每次迭代都冲过最小值。

同样地,有时也可能看到这样形状的 J ( θ ) J(\theta) J(θ)
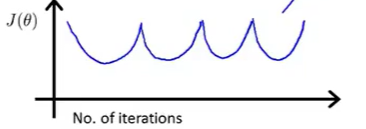
解决的办法也是采用一个较小的学习率 α \alpha α。
学习率 α \alpha α
已经有证明,如果学习率 α \alpha α 足够小,那么每次迭代之后的代价函数 J ( θ ) J(\theta) J(θ) 都会下降。但是有时候也不希望学习率太小,那样的话梯度下降算法可能收敛得很慢。
因此选择学习率可以尝试一系列 α \alpha α 值,
比如 0.001 , 0.01 , 0.1 , 1.... 0.001, 0.01, 0.1, 1.... 0.001,0.01,0.1,1....,每隔十倍取一个值,然后绘制的 J ( θ ) J(\theta) J(θ) 随着迭代步数变化的曲线,然后选择使 J ( θ ) J(\theta) J(θ) 快速下降的一个 α \alpha α 值。
特征与多项式回归(Polynomial regression)
可以使线性回归的方法拟合非常复杂的函数,甚至是非线性函数。
正规方程(Normal equation)
对于某些线性回归问题,它会给提供更好的方法来求参数 θ \theta θ 的最优值。
梯度下降法经过多次迭代来收敛代价函数 J ( θ ) J(\theta) J(θ) 到全局最小值,而正规方法提供了一种求 θ \theta θ 的解析解法。这样就不需要进行多次迭代,而是可以一次性求解 θ \theta θ 的最优值。
如果我们使用正规方程,我们就不需要特征缩放。
但是,如果使用的是梯度下降法,特征缩放就非常重要了。
Example

X m × ( n + 1 ) , y m × 1 X_{m×(n+1)}, y_{m×1} Xm×(n+1),ym×1
θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy
将上面的例子用 Octave 工具演示:

梯度下降法与正规方程法比较
| 梯度下降法 | 正规方程法 | |
|---|---|---|
| 缺点 | 1.需要选择学习率 α \alpha α。所以通常需要运行多次来尝试不同的学习率 2.需要更多次的迭代(取决于具体细节,计算可能会很慢)。 |
正规方程法为了求解参数 θ \theta θ 需要求解 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1,而 X T X X^TX XTX 是一个 n × n n×n n×n 的矩阵,对于大多数计算应用来说,实现逆矩阵的计算代价以矩阵维度的三次方增长 O ( n 3 ) O(n^3) O(n3) 。因此,如果特征变量 n n n 的数目很大的话,计算这个逆矩阵的代价是非常大的。此时计算速度也会非常慢。 |
| 优点 | 梯度下降法在特征变量很多的情况下,上百万个特征变量也能很好运行。 | 1.不需要现在学习速率α,所有这就会很方便。 2.不需要迭代,所以不需要画出 J ( θ ) J(\theta) J(θ) 的曲线来检查收敛性,或者采取任何的额外步骤。 |
所以,特征数量 n n n 上万时,用正规方程法的求解速度会开始变得有点慢,此时可能梯度下降法会好点。
正规方程法在矩阵不可逆情况下的解决方法
当我们计算 θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy 的时候,万一矩阵 X T X X^TX XTX 是不可逆的话怎么办?
我们称不可逆的矩阵称为奇异或退化矩阵。
在 Octave 里有两个函数可以求解矩阵的逆,一个被称为 pinv,另一个被称为 inv。但是只要你使用 pinv 函数,它就能计算出你想要的θ值(即使矩阵 X T X X^TX XTX 不可逆)。
矩阵 X T X X^TX XTX 不可逆两种最常见的原因
- 学习问题包含了多余的特征,比如房价信息样本集中其中一个特征为平方英尺面积,同时还有一个特征为平方米面积,因为平方英尺与平方米成对应成比例,显然 X T X X^TX XTX 不可逆。
- 你在运行的学习算法有很多特征值 ( m ≤ n ) (m≤n) (m≤n),样本数量过少了。
矩阵 X T X X^TX XTX 是奇异矩阵或者是不可逆矩阵解决方法:
- 看特征里是否有一些多余的特征。
类似在上面举的平方米和平方英尺,是线性相关的或者互为线性函数的。如果确实有一些多余的特征,我们可以删除其中一个,无须两个特征都保留。删除至没有多余的特征为止。 - 如果没有多余的特征,就要检查是不是有过多的特征。
如果特征数实在太多了,在少一些不影响的情况下,可以删除一些特征或者考虑使用正规化方法。
正规方程法公式 θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy 推导过程
J ( θ ) J(\theta) J(θ) 对 θ \theta θ求导,并令其为 0 0 0