8.4 假设问题的进一步说明
例如当问到是否购入某批灯泡(根据其寿命)::
H 0 : μ ≥ 1000 h o u r 认 为 该 厂 生 产 的 灯 泡 【 不 会 低 于 】 规 定 的 质 量 标 准 1000 小 时 和 H 0 : μ ≤ 1000 h o u r 认 为 该 厂 生 产 的 灯 泡 【 可 能 低 于 】 规 定 的 质 量 标 准 1000 小 时 H_0: \mu \ge 1000 \; hour \qquad 认为该厂生产的灯泡【不会低于】规定的质量标准1000小时\\ 和\\ H_0: \mu \le 1000 \;hour \qquad 认为该厂生产的灯泡【可能低于】规定的质量标准1000小时 H0:μ≥1000hour认为该厂生产的灯泡【不会低于】规定的质量标准1000小时和H0:μ≤1000hour认为该厂生产的灯泡【可能低于】规定的质量标准1000小时
同一个问题,有两种假设,而这两种假设会导致出现不同的结果,那么究竟该如何确定原假设 H 0 H_0 H0和备择假设 H 1 H_1 H1呢。下面给出了很好的解释:
- 在假设检验中一般是把希望证明的命题放在备择假设 H 1 H_1 H1上;而把原有的、传统的观点或结论放在原假设 H 0 H_0 H0上。
- 所谓“原有的、传统的”是指原有的理论、原有的看法、原有的状况,或者说是那些历史的、经验的、被大多数人认可和接受的东西,在没有充分证据证明其错误时,总是假定是正确的,处于原假设 H 0 H_0 H0被保护的位置。
- 而那些新的、可能的 、猜测的东西,希望用事实推翻原假设,得到船新的观点,处在备择假设 H 1 H_1 H1的位置。
- 接受备择假设 H 1 H_1 H1一定意味着原假设 H 0 H_0 H0错误;而没有拒绝原假设 H 0 H_0 H0并不能表明备择假设 H 1 H_1 H1一定是错的。
提出各类假设的例子:
很多假设检验类型既有单侧检验又有双侧检验,这里只是给出如何建立假设的统计量和统计值的符号,而对于是大于小于还是等于就不具体都一一举例了(例如 H 0 : μ = 1000 和 H 0 : μ ≥ 0.81 H_0:\mu = 1000 和 H_0:\mu \ge 0.81 H0:μ=1000和H0:μ≥0.81 这两种形式)。
第八章 假设检验
- 一个总体参数的检验
- 总体均值的检验(z或t检验)

- 双侧检验
H 0 : μ = μ 0 没 有 显 著 差 别 H 1 : μ ≠ μ 0 有 显 著 差 别 H_0: \mu = \mu_0 \qquad 没有显著差别 \\ H_1: \mu \ne \mu_0 \qquad\quad 有显著差别 H0:μ=μ0没有显著差别H1:μ=μ0有显著差别 - 左单侧检验
H 0 : μ ≥ μ 0 没 有 显 著 差 别 H 1 : μ < μ 0 有 显 著 差 别 H_0: \mu \ge \mu_0 \qquad 没有显著差别 \\ H_1: \mu < \mu_0 \qquad\quad 有显著差别 H0:μ≥μ0没有显著差别H1:μ<μ0有显著差别 - 右单侧检验
H 0 : μ ≤ μ 0 没 有 显 著 差 别 H 1 : μ > μ 0 有 显 著 差 别 H_0: \mu \le \mu_0 \qquad 没有显著差别 \\ H_1: \mu > \mu_0 \qquad\quad 有显著差别 H0:μ≤μ0没有显著差别H1:μ>μ0有显著差别
- 双侧检验
- 总体比例的检验(z或t检验)

H 0 : π = π 0 支 持 该 比 例 H 1 : π ≠ π 0 不 支 持 该 比 例 H_0: \pi = \pi_0 \qquad\quad支持该比例\\ H_1: \pi \ne \pi_0 \qquad不支持该比例 H0:π=π0支持该比例H1:π=π0不支持该比例 - 总体方差的检验( χ 2 \chi^2 χ2检验)
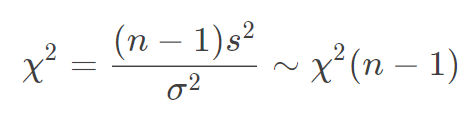
H 0 : σ 2 ≤ σ 0 2 在 误 差 以 内 H 1 : σ 2 > σ 0 2 在 误 差 以 外 H_0:\sigma^2 \le \sigma_0^2 \qquad在误差以内 \\ H_1:\sigma^2 > \sigma_0^2 \qquad在误差以外 H0:σ2≤σ02在误差以内H1:σ2>σ02在误差以外
- 总体均值的检验(z或t检验)
- 两个总体参数的检验
- 两个总体均值之差的检验(z或t检验)
- 总体标准差已知:
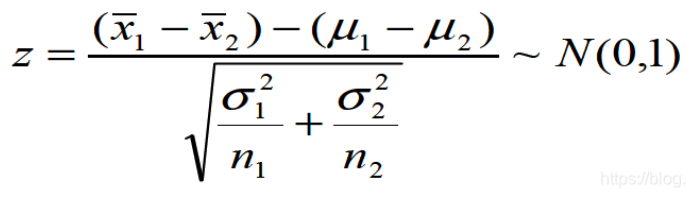
- 总体标准差未知:
- 方差相等:
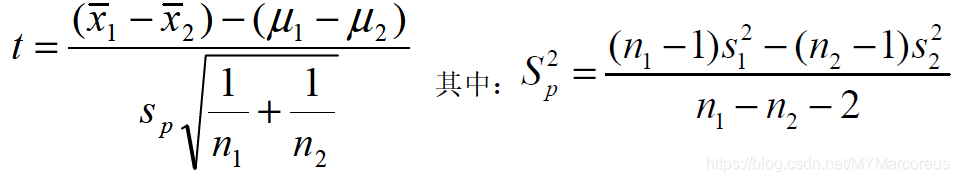
- 方差不相等:

H 0 : μ 1 − μ 2 = 0 H 1 : μ 1 − μ 2 ≠ 0 H_0: \mu_1 - \mu_2 = 0\\ H_1:\mu_1 - \mu_2 \ne 0 H0:μ1−μ2=0H1:μ1−μ2=0
- 方差相等:
- 总体标准差已知:
- 两个总体比例之差的检验(z检验)
- 检验两个总体比例相等:
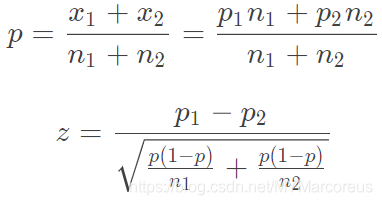
H 0 : π 1 − π 2 = 0 H 1 : π 1 − π 2 ≠ 0 H_0: \pi_1 - \pi_2 = 0\\ H_1:\pi_1 - \pi_2 \ne 0 H0:π1−π2=0H1:π1−π2=0 - 检验两个总体比例之差不为零:
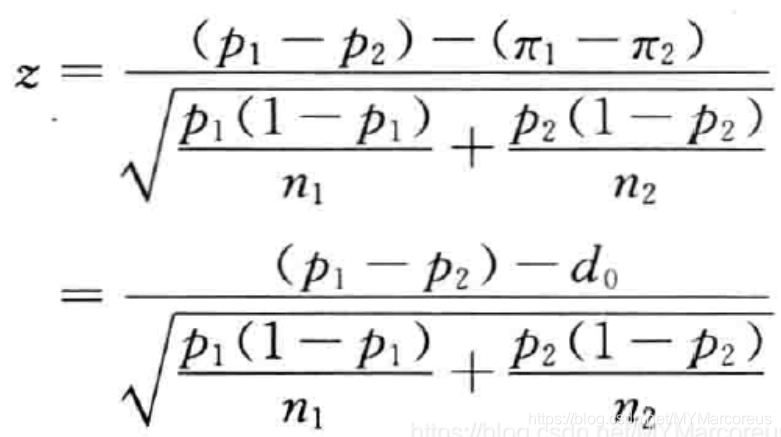
H 0 : π 1 − π 2 ≥ 10 % H 1 : π 1 − π 2 < 10 % H_0: \pi_1 - \pi_2 \ge 10\%\\ H_1:\pi_1 - \pi_2 < 10\% H0:π1−π2≥10%H1:π1−π2<10%
- 检验两个总体比例相等:
- 两个总体方差比的检验 (F检验)

H 0 : σ 1 / σ 2 = 1 H 1 : σ 1 / σ 2 ≠ 1 H_0: \sigma_1/\sigma_2 = 1\\ H_1:\sigma_1/\sigma_2 \ne 1 H0:σ1/σ2=1H1:σ1/σ2=1
- 两个总体均值之差的检验(z或t检验)
第九章 分类数据分析
- 拟合优度检验( χ 2 \chi^2 χ2检验)
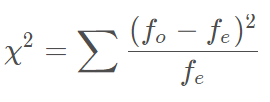
H 0 : 观 察 频 数 和 期 望 频 数 一 致 H 1 : 观 察 频 数 和 期 望 频 数 不 一 致 H_0: 观察频数和期望频数\quad一致\\ H_1: 观察频数和期望频数不一致 H0:观察频数和期望频数一致H1:观察频数和期望频数不一致 - 独立性检验( χ 2 \chi^2 χ2检验)
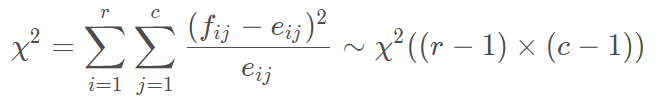
H 0 : 行 变 量 和 列 变 量 相 互 独 立 H 1 : 行 变 量 和 列 变 量 不 相 互 独 立 H_0: 行变量和列变量\quad相互独立\\ H_1: 行变量和列变量不相互独立 H0:行变量和列变量相互独立H1:行变量和列变量不相互独立
第十章 方差分析
- 单因素方差分析(F检验)
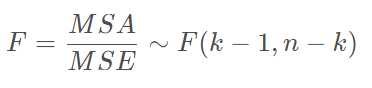
在方差分析中,原假设所描述的是在按照自变量的取值分成的类中,因变量的均值是否相等。因此,检验k个水平(总体)的均值是否相等,需要提出如下形式的假设(得到的结果一般都是拒绝原假设,从而有显著影响):
H 0 : μ 1 = μ 2 = . . . = μ k 自 变 量 对 因 变 量 没 有 显 著 影 响 H 1 : μ ( i = 1 , 2 , . . . , k ) 不 全 相 等 自 变 量 对 因 变 量 有 显 著 影 响 H_0:\mu_1 = \mu_2 = ... = \mu_k \qquad\qquad\qquad 自变量对因变量没有显著影响 \\ H_1:\mu_(i = 1,2,...,k)不全相等 \;\quad\qquad 自变量对因变量\quad有显著影响 H0:μ1=μ2=...=μk自变量对因变量没有显著影响H1:μ(i=1,2,...,k)不全相等自变量对因变量有显著影响 - 双因素方差分析 (F检验)

有无交互作用的都假设的提出都是类似的。
为了检验两个因素的影响,需要对两个因素分别提出假设(k为行因素的水平个数,r为列因素水平个数):- 对行因素提出的假设为:
H 0 : μ 1 = μ 2 = . . . = μ k 自 变 量 ( 行 变 量 ) 对 因 变 量 没 有 显 著 影 响 H 1 : μ ( i = 1 , 2 , . . . , k ) 不 全 相 等 自 变 量 ( 行 变 量 ) 对 因 变 量 有 显 著 影 响 H_0:\mu_1 = \mu_2 = ... = \mu_k \qquad\qquad\qquad 自变量(行变量)对因变量没有显著影响 \\ H_1:\mu_(i = 1,2,...,k)不全相等 \;\quad\qquad 自变量(行变量)对因变量\quad有显著影响 H0:μ1=μ2=...=μk自变量(行变量)对因变量没有显著影响H1:μ(i=1,2,...,k)不全相等自变量(行变量)对因变量有显著影响 - 对列因素提出的假设为:
H 0 : μ 1 = μ 2 = . . . = μ r 自 变 量 ( 列 变 量 ) 对 因 变 量 没 有 显 著 影 响 H 1 : μ ( i = 1 , 2 , . . . , r ) 不 全 相 等 自 变 量 ( 列 变 量 ) 对 因 变 量 有 显 著 影 响 H_0:\mu_1 = \mu_2 = ... = \mu_r \qquad\qquad\qquad 自变量(列变量)对因变量没有显著影响 \\ H_1:\mu_(i = 1,2,...,r)不全相等 \;\quad\qquad 自变量(列变量)对因变量\quad有显著影响 H0:μ1=μ2=...=μr自变量(列变量)对因变量没有显著影响H1:μ(i=1,2,...,r)不全相等自变量(列变量)对因变量有显著影响
- 对行因素提出的假设为:
第十一章 一元线性回归
- 相关关系的显著性检验(t检验)

H 0 : ρ = 0 两 个 变 量 之 间 不 存 在 显 著 的 线 性 关 系 H 1 : ρ ≠ 0 两 个 变 量 之 间 存 在 显 著 的 线 性 关 系 H_0: ρ = 0 \qquad两个变量之间不存在显著的线性关系 \\ H_1: ρ \ne 0 \qquad两个变量之间\quad存在显著的线性关系 H0:ρ=0两个变量之间不存在显著的线性关系H1:ρ=0两个变量之间存在显著的线性关系 - 线性关系的显著性检验(F检验)
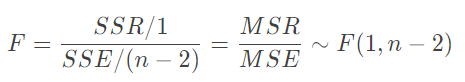
H 0 : β 1 = 0 两 个 变 量 之 间 不 存 在 显 著 的 线 性 关 系 H 1 : β 1 ≠ 0 两 个 变 量 之 间 存 在 显 著 的 线 性 关 系 H_0: \beta_1 = 0\qquad两个变量之间不存在显著的线性关系 \\ H_1: \beta_1 \ne 0 \qquad两个变量之间\quad存在显著的线性关系 H0:β1=0两个变量之间不存在显著的线性关系H1:β1=0两个变量之间存在显著的线性关系 - 回归系数的显著性检验(t检验或F检验)

H 0 : β 1 = 0 没 有 证 据 表 明 自 变 量 x 对 因 变 量 y 影 响 显 著 H 1 : β 1 ≠ 0 表 明 自 变 量 x 对 因 变 量 y 影 响 显 著 H_0: \beta_1 = 0\qquad 没有证据表明自变量x对因变量y影响显著 \\ H_1: \beta_1 \ne 0 \quad\qquad \quad\qquad 表明自变量x对因变量y影响显著 H0:β1=0没有证据表明自变量x对因变量y影响显著H1:β1=0表明自变量x对因变量y影响显著
第十二章 多元线性回归
- 线性关系的显著性检验(F检验)

H 0 : β 1 = β 2 = . . . = β k = 0 y 与 k 个 自 变 量 之 间 不 存 在 显 著 的 线 性 关 系 H 1 : β 1 , β 2 , . . . , β k 至 少 一 个 不 等 于 0 y 与 k 个 自 变 量 之 间 存 在 显 著 的 线 性 关 系 H_0: \beta_1 = \beta_2 =...=\beta_k = 0 \qquad\qquad\quad y与k个自变量之间不存在显著的线性关系 \\ H_1: \beta_1, \beta_2,...,\beta_k至少一个不等于0 \qquad y与k个自变量之间\quad存在显著的线性关系 H0:β1=β2=...=βk=0y与k个自变量之间不存在显著的线性关系H1:β1,β2,...,βk至少一个不等于0y与k个自变量之间存在显著的线性关系 - 回归系数的显著性检验(t检验)
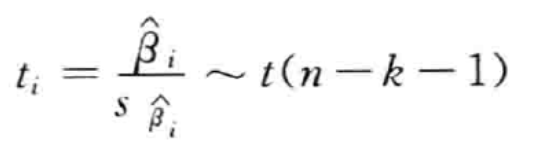
对 任 意 β i ( i = 1 ∼ k ) 有 : H 0 : β i = 0 y 与 第 i 个 自 变 量 x i 不 存 在 显 著 的 线 性 关 系 H 1 : β i ≠ 0 y 与 第 i 个 自 变 量 x i 存 在 显 著 的 线 性 关 系 对任意\beta_i (i = 1\sim k)有:\\ H_0: \beta_i = 0 \qquad y与第i个自变量x_i不存在显著的线性关系\\ H_1: \beta_i \ne 0 \qquad y与第i个自变量x_i\quad存在显著的线性关系 对任意βi(i=1∼k)有:H0:βi=0y与第i个自变量xi不存在显著的线性关系H1:βi=0y与第i个自变量xi存在显著的线性关系