使用 Trapezoidal Rule（梯形法则）求积分

Trapezoidal Rule

思想原理

为了求解积分值，人们想到一种近似方法。假设要求 $f(x)$ 在 $[a,b]$ 上的积分，将积分区间等长分成 $n$ 段，则每两个分段点之间的距离 $h=\frac{b-a}{n}$，然后如下图进行近似

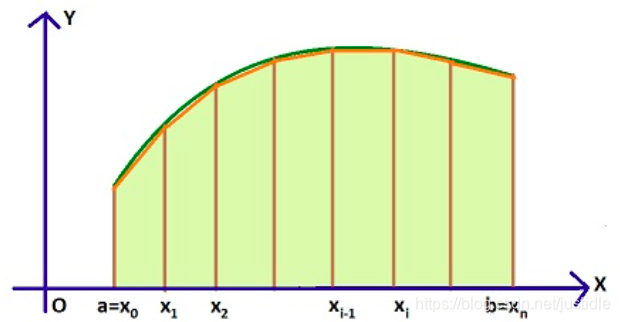
则该区间上的积分值就近似等同于每个小梯形的面积之和。

推导过程

如上图所示，${\int }_a^{b}f(x)$ 的结果，就是上图中所有梯形面积总和。

梯形面积

第一个梯形（最左边）的上底 $f(x_0)$，下底 $f(x_1)$，高为 $h=\frac{b-a}{n}$，因此对应的面积为 $S_1=(f(x_0)+f(x_1))\ast h/2=\frac{(f(x_0)+f(x_1))\ast h}{2}$。
以此类推，最后一个（最右边）的上上底 $f(x_{n-1})$，下底 $f(x_n)$，高为 $h=\frac{b-a}{n}$，因此对应的面积为 $S_n=(f(x_{n-1})+f(x_n))\ast h/2=\frac{(f(x_{n-1})+f(x_n))\ast h}{2}$。
因此，所有梯形的总面积为
$$\begin{gathered} {\int }_a^{b}f(x)\approx \sum _{i=1}^n(S_i)=S_0+...+S_n \\ =\frac{h}{2}[f(x_0)+f(x_1)+f(x_1)+f(x_2)+\cdots +f(x_{n-2})+f(x_{n-1})+f(x_{n-1})+f(x_n)] \\ =\frac{(b-a)}{2\ast n}[f(x_0)+2\sum _{i=1}^{n}f(x_i)+f(x_n)] \end{gathered}$$

C++ implement

输入

根据上面的公式，我们可以总结出，输入包括以下几个：
1、$f(x)$。即需要积分的函数。
2、$x_0$。即积分开始点。
3、$x_n$。即积分结束点。
4、$n$。即毕竟的次数。

$f(x)$ 函数

和前面的设计一样，使用外部函数实现。对应的函数原型如下：

//输入x，计算对应的y值。
double f(double x);

主框架

类似前面的计算，主要用于输入数据。

#include <iostream>
using namespace std;

//输入x，计算对应的y值。
double f(double x);

int main() {
    
    
	//变量定义
	double lower;//起点坐标
	double upper;//终点坐标
	int step;//迭代次数
	
	cout<<"Enter lower limit of integration:";
	cin>>lower;
	cout<<"Enter upper limit of integration:";
	cin>>upper;
	cout<<"Enter number of sub intervals:";
	cin>>step;

	//计算 h
	double h=(upper-lower)/step;
	//计算f(x0)+f(xn)
	double ans=f(lower)+f(upper);
	//开始迭代
	double x=lower;
	for (int i=1; i<step; i++) {
    
    
		x += h;
		ans += 2*f(x);
	}
	ans = ans*h/2;

	//结果输出
	cout<<"Required value of integration is: "<<ans<<"\n";
	
	return 0;
}

测试

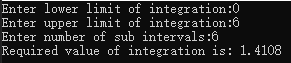
样例 1

我们计算 ${\int }_0^6\frac{1}{1+x^2}$，迭代次数为 $6$ 次。

$f(x)$ 函数实现

#include <cmath>
//输入x，计算对应的y值。
double f(double x) {
    
    
    return 1.0/(1+pow(x,2));
}

编译

测试环境为 Win10+MinGW，使用 g++ 编译器。

g++ -g -o TR.exe main.cpp f.cpp

运行结果