一、数学原理
在变步长的复化梯形计算过程中运用:
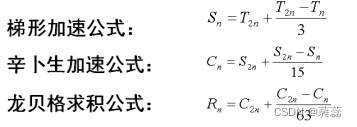
就能将粗糙的梯形值Tn逐步加工成精度较高的辛普森值Sn、柯特斯值Cn和龙贝格值Rn。或者说,将收敛缓慢的梯形值序列Tn加工成收敛迅速的龙贝格值序列Rn,这种线性外推的加速方法称为龙贝格算法(龙贝格公式),其通用计算公式为:
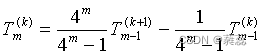
二、实验内容
%脚本文件,调用romberg函数求积分sin(x^2)/x
format compact
clc,clear,ep=1e-4;
fun=@(x)sin(x.^2)./x;
[t,T]=romberg(fun,1e-6,1,ep);
disp('龙贝格求积T表如下:');
digits(7);B=vpa(T);
disp(B);
y1=vpa(t);
y2=vpa(integral(fun,1e-6,1));
disp('龙贝格求积公式求积结果:');fprintf('%c', 8);
disp(y1);
disp(' 精确值参考:');fprintf('%c', 8);
disp(y2);
%龙贝格算法函数文件
function [t,T]=romberg(fname,a,b,e)
format long
if nargin<4
e=1e-4;
end
i=1;j=1;h=b-a;
T(i,1)=(fname(a)+fname(b))*h/2; % 梯形计算
T(i+1,1)=T(i,1)/2+sum(feval(fname,a+h/2:b-h/2+0.001*h))*h/2;
T(i+1,j+1)=4^j*T(i+1,j)/(4^j-1)-T(i,j)/(4^j-1);
while abs(T(i+1,i+1)-T(i,i))>e
i=i+1;h=h/2;
T(i+1,1)=T(i,1)/2+sum(feval(fname,a+h/2:h:b-h/2+0.001*h))*h/2;
for j=1:i
T(i+1,j+1)=4^j*T(i+1,j)/(4^j-1)-T(i,j)/(4^j-1);
end
end
t=T(i+1,j+1);
三、实验结果与分析
龙贝格算法运行结果:
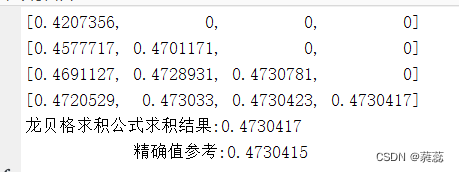
通过步长的变化-折半和线性外推法,可以将梯形公式、辛普森公式以及柯特斯公式联系起来,使得精度迅速提高,这就是龙贝格算法的思想,也称为理查森线性外推算法。从计算过程可以得出,只计算了4次的复化梯形求积,但是通过外推技巧,其计算结果从只有 位有效数字提升到 位有效数字,其计算精度有了大幅提升,而计算量增加不多。