CART

CART的全称是Classification and Regression Tree, 即分类与回归树, 其既可用于分类也可用于回归.
CART本质是对特征空间进行二元划分(即CART生成的决策树是一棵二叉树),它能够对类别变量与连续变量进行分裂,大体的分割思路是：

先对某一维数据进行排序(这也是为什么我们对无序的类别变量进行编码的原因）
然后对已经排好后的特征进行切分,切分的方法就是if … else …的格式.
然后计算衡量指标(分类树用Gini指数,回归树用最小平方值),最终通过指标的计算确定最后的划分点, 然后按照下面的规则生成左右子树： If x < A: Then go to left; else: go to right.

回归树

平方误差最小化

给定训练集 $D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\}$

采用启发式搜索，选择第 j 个特征 $x^{(j)}$ 和它取的值s，分别作为切分特征和切分点，并将划分的结果分为两个区域：
$R_{1}(j, s)=\left\{x \mid x^{(j)} \leqslant s\right\} \text { 和 } R_{2}(j, s)=\left\{x \mid x^{(j)}>s\right\}$
然后寻找最优切分特征 j 和最优切分点 s ，即求解：
$\min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right]$
因为最小二乘法，区域 $R_m$ 最优值即标签 $y_i$ 的均值：
$\hat{c}_{m}=\frac{1}{N_{m}} \sum_{x_{i} \in R_{m}(j, s)} y_{i}, \text { 其中 } m=1,2$
遍历所有的切分变量和切分点，可以找到最优的切分变量和切分点，构成对 (j, s),然后对每个区域重复上述过程，直到满足停止条件。
回归树生成后，将输入空间划分为 M 个单元 $R_{1}, R_{2}, \ldots R_{M}$ ，即 M 个叶子节点，每个单元 $R_m$ 都有一个固定的输出值 $c_m$ ，回归模型可以表示为：
$f(x)=\sum_{m=1}^{M} c_{m} I\left(x \in R_{m}\right)$

分类树

基尼指数

假设分布有 K 类，样本点属于第k类的概率为 $p_k$ ，则概率分布定义的基尼指数为：
$\operatorname{Gini}(p)=\sum_{k=1}^{K} p_{k}\left(1-p_{k}\right)=1-\sum_{k=1}^{K} p_{k}^{2}$
对于样本集D，其基尼指数为：
$\operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2}$
这里， $C_k$ 是D中属于第 k 类的样本子集，K是类的个数。

 可以看出，如果D中样本分布越不均衡，基尼系数越小，直到仅有一类时，值为零；分布越平衡，基尼系数越大。

如果样本集合 D 根据特征 A 是否取某一可能值 a 被分割成 $D_1$ 和 $D_2$ 两部分， $D_{1}=\{(x, y) \in D \mid A(x)=a\}, \quad D_{2}=D-D_{1}$
则在特征 A 的条件下，集合 D 的基尼指数定义为：
$\operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)$

在所有可能的特征 A 以及它们所有可能的切分点 s 中，选择基尼指数最小的特征即其对应的切分点作为最优特征和最优切分点，从而从当前节点分裂成两个子结点，将训练数据集依特征分配到两个子结点中去.
重复分裂过程直至满足停止条件。

ID3

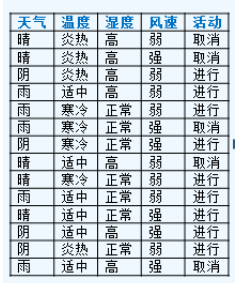
在这里插入图片描述

基本概念

信息：

$x_i$ 的信息为 $L(x_i)=-log_2(p(xi)), p(xi)$ 为选择该分类的概率.

熵Entropy:

即为信息期望值 $H(D)=-\sum_{k=1}^{K} p_{k} \log _{2} p_{k}$
K是分类数目
在这里插入图片描述

条件熵 conditional entropy

$\begin{aligned} H(D \mid A) &=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right) \\ &=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \end{aligned}$
$D_i$ 为由特征A划分的第i个子集的大小， $D_{ik}$ 为第i个子集中属于第k类的样本数
在这里插入图片描述

信息增益

特征A对训练数据集D的信息增益g(D,A), 定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即 $g (D, A) = H (D) - H (D ∣ A)$
在这里插入图片描述

流程

如果每一分支下分类class相同，或仅有最后一种特征（赞成多数表决法）则返回 class，否则求最佳划分方式（信息增益最大）的特征索引，以该特征列对应的标签为根（键），建立树（键值），遍历该特征列（无重复）将划分后的特征余子式和标签子列重复上述操作，递归出整个树。

C4.5

以信息增益率代替信息增益

与ID3的不同

属性分裂信息度量H

$\text {Split-Information}(D, A)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \log _{2} \frac{\left|D_{i}\right|}{|D|}$
在这里插入图片描述

信息增益率

IGR = Gain / H
其中Gain为信息增益，H为属性分裂信息度量
在这里插入图片描述

流程

while（当前节点“不纯”）
1.计算当前节点的类别熵Info（D）（以类别取值计算）
2.计算当前节点的属性熵Info（Ai）（按照属性取值下的类别取值计算）
3.计算各个属性的信息增益 Gain（Ai）=Info（D）-Info（Ai）
4.计算各个属性的分类信息度量日H(Ai)（按照属性取值计算）
5.计算各个属性的信息增益率IGR=Gain（Ai）/H（Ai）
end while
当前节点设置为叶子节点

CART与ID3、C4.5决策树