刷穿LeetCode——Task08

这篇博客记录刷题第8天的解题思路与心得。

64.不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7 输出：28

示例 2：

输入：m = 3, n = 2 输出：3 解释： 从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 3：

输入：m = 7, n = 3 输出：28

示例 4：

输入：m = 3, n = 3 输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109

分析：每次机器人只能向右或者向下移动一步，设 $f(i,j)$ 为从左上角走到$(i,j)$的路径数量，则 $f(i,j)$ 仅由 同列上一行 $f(i-1,j)$ 和同行前一列 $f(i,j-1)$决定，动态规划转移方程为：$$f(i,j)=f(i-1,j)+f(i,j-1)$$

• 如果构造一个二维数组记录路径数量，考虑到有 $i-1$和$j-1$存在，我们，则第一行 $f(0,j)$ 和 第一列$f(i,0)$ 需要置1。官方题解如下：

class Solution {
    
    
public:
    int uniquePaths(int m, int n) {
    
    
        vector<vector<int>> f(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
    
    
            f[i][0] = 1;
        }
        for (int j = 0; j < n; ++j) {
    
    
            f[0][j] = 1;
        }
        for (int i = 1; i < m; ++i) {
    
    
            for (int j = 1; j < n; ++j) {
    
    
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
};

• 注意到 $f(i,j)$ 仅与当前行以及上一行（或者当前列与上一列）状态有关，且由于我们交换行列的值并不会对答案产生影响，即$f(i,j)=f(j,i)$，因此我们总可以构造包含较小维数的一维滚动数组$f(i)$来替代二维数组。不妨令行数 $m$ 较大，列数 $n$ 较小，这样每一行都对列遍历$f(i)=f(i-1)+f(i)$，在不同行之间滚动。这种做法空间复杂度减小为 $min(m,n)$。

class Solution {
    
    
public:
    int uniquePaths(int m, int n) {
    
    
        int temp;
        if (m < n) {
    
                     //选择n=min(m, n), m=max(m, n)
            temp = m; 
            m = n; n = temp;
        }
        int d[n];                   //滚动数组替代二维数组
        for (int i = 0; i < n; i++) 
            d [i] = 1;            //初始化原二维数组第1行、第1列
        for (int i = 1; i < m; i++) {
    
    
            for (int j = 1; j < n; j++) {
    
    
                d[j] += d[j-1];  //当前列d[j]状态仅与j-1、j列有关
            }
        }
        return d[n-1];      
    }
};

• 这题其实也算排列组合的题，机器人一定会走m+n-2步，即从m+n-2中挑出m-1步向下走不就行，一共有 $C(m+n-2,m-1)$种走法，公式法如下：
  

class Solution {
    
    
public:
    int uniquePaths(int m, int n) {
    
    
        long long ans = 1;
        for (int x = n, y = 1; y < m; ++x, ++y) {
    
    
            ans = ans * x / y;
        }
        return ans;
    }
};

70.爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2 输出： 2 解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： 3 输出： 3 解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

分析：

• 令 $f(i)$ 表示爬 $i$ 阶楼梯的爬法，每次只能爬1阶或2阶楼梯，则可以从 $i-1$阶爬 1 阶，或者 $i-2$ 阶爬 2 阶上来，容易得到：$$f(i)=f(i-1)+f(i-2)$$
  这便是斐波那契数列，我们可以构造含$n+1$个元素的一维数组依次求解 $f(i)$，如下：

class Solution {
    
    
public:
    int climbStairs(int n) {
    
    
        if (n < 2)  return n;
        int* f = new int [n+1];   //第i阶楼梯对应数组第i个下标
        f[0] = 1; 
        f[1] = 1;
        for (int i = 2; i <= n; i++) {
    
    
            f[i] = f[i-1] + f[i-2];
        }
        return f[n];
        delete []f;
    }
};

• 为减少空间复杂度，也可以用仅含有3个元素的滚动数组求解斐波那契数列数列，见参考[1]；不用数组，也可以直接用三个变量求解不同阶楼梯的爬法，如下：

class Solution {
    
    
public:
    int climbStairs(int n) {
    
    
        if (n < 2)  
            return n;
        int n1 = 1, n2 = 1;
        int temp;
        for (int i = 2; i <= n; i++) {
    
    
            temp = n2; 
            n2 = n1 + n2;
            n1 = temp; 
        }
        return n2;
    }
};

78. 子集

给你一个整数数组 nums ，返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。

示例 1：

输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0] 输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10

分析： 这题和全排列一样，首先想到的就是用回溯法求解。回溯法是深度遍历搜索 (DFS) 的一种，而DFS需要调用递归。参照题解区大佬的分析归纳[3]：

怎么样写回溯算法(从上而下，※代表难点，根据题目而变化)
①画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
②根据题意，确立结束条件
③找准选择列表(与函数参数相关),与第一步紧密关联※
④判断是否需要剪枝
⑤作出选择，递归调用，进入下一层
⑥撤销选择

1. 递归树
   

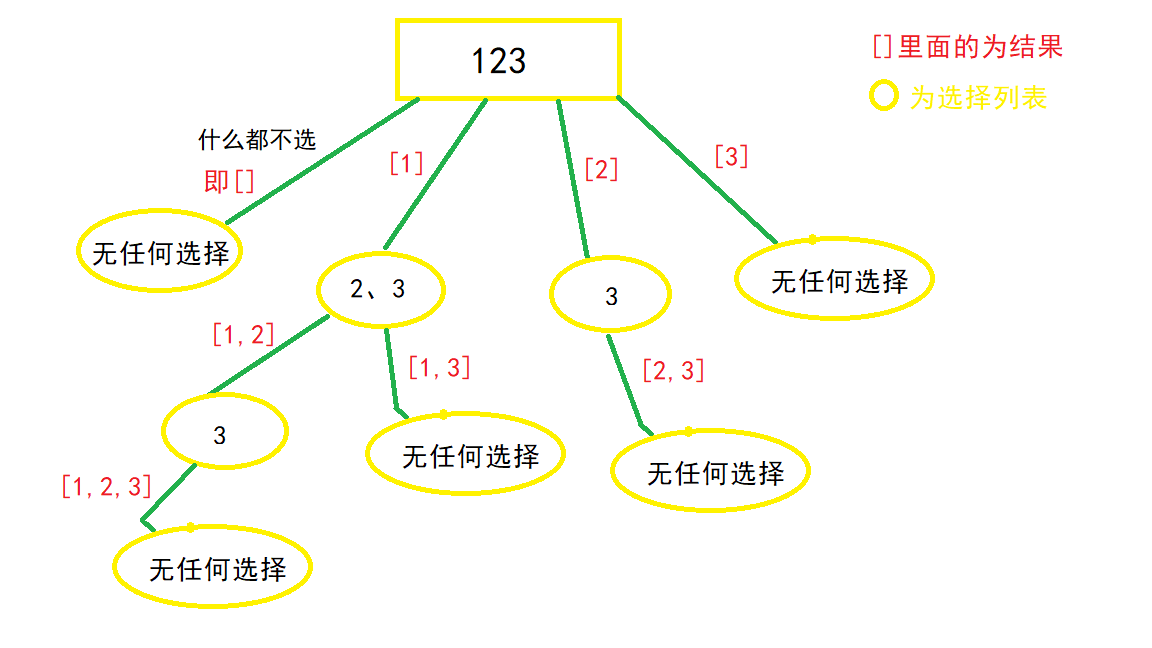
观察上图可得，选择列表里的数，都是选择路径(红色框)后面的数，比如[1]这条路径，他后面的选择列表只有"2、3"，[2]这条路径后面只有"3"这个选择，那么这个时候，就应该使用一个状态变量记录在数组中的当前位置（递归树第一层）。

2. 找结束条件

此题非常特殊，所有路径都应该加入结果集，所以不存在结束条件。或者说当 cur 参数越过数组边界的时候，程序就自己跳过下一层递归了，因此不需要手写结束条件,直接加入结果集

3. 找选择列表

子集问题的选择列表，是上一条选择路径之后的数, 即

for(int i=cur; i<nums.size(); i++)

4. 判断是否需要剪枝

从递归树中看到，路径没有重复的，也没有不符合条件的，所以不需要剪枝

5. 做出选择(即for 循环里面的)

6. 撤销选择

具体C++代码如下：

class Solution {
    
    
public:
    vector<vector<int>> subsets(vector<int>& nums) {
    
    
        vector<vector<int>> res;
        vector<int> path;                         //状态变量：记录选了哪些数
        int cur = 0;                              //状态变量：记录在数组中当前位置
        dfs(cur, nums, path, res);
        return res;
    }

private:
    void dfs(int cur, vector<int>& nums, vector<int>& path, vector<vector<int>>& res) {
    
    
        res.push_back(path);                       
        for (int i = cur; i < nums.size(); i++)    //选择列表
        {
    
    
            path.push_back(nums[i]);              //选择当前节点
            dfs(i + 1, nums, path, res);         //递归做深度优先搜索
            path.pop_back();                     //撤销选择
        }
    } 
};

输入:
[1,2,3]
输出:
[[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3]]
预期结果:
[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

附录：回溯问题类型归纳如下：

参考

[1] 小技巧—滚动数组
[2] C++中数组定义及初始化
[3] C++ 总结了回溯问题类型 带你搞懂回溯算法(大量例题)