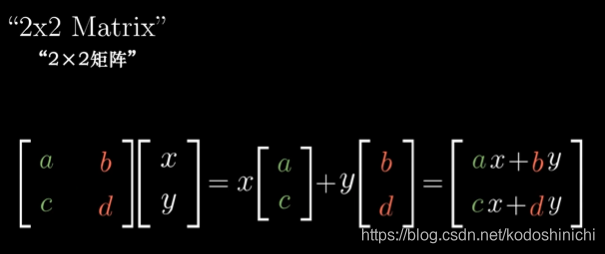矩阵与线性方程组-思维导图

线性变换的定义
1.变换与函数
所谓变换就是函数的另一种名称,它接收输入,然后输出对应的结果。
只不过在线性代数的语境下,输入与输出的都是向量
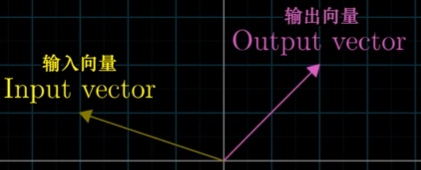
2.使用“变换”这一名词的原因
暗示读者用特定的方式来可视化这种输入与输出的映射关系——一种运动的观点
对某一个变量进行变换,就可以理解为将一个变换移动旋转到输出向量的位置
要对整个变换进行理解,则考虑将空间中所有向量都按照既定的移动方式进行改变
3.线性变换:具有以下性质的变换
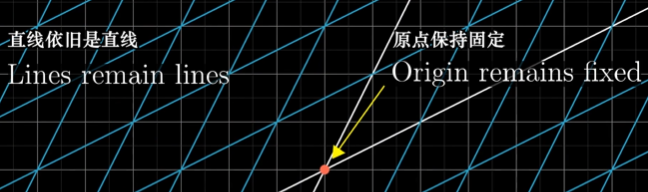
①直线在变换后仍然为直线
②原点在变换过程中保持不变
总的来说:可以把线性变换看做是“保持网格线平行且等距分布”的变换
线性变换的数值描述

1.使用四个数值(两个二维基向量的坐标)即可以完全表述一个线性变换
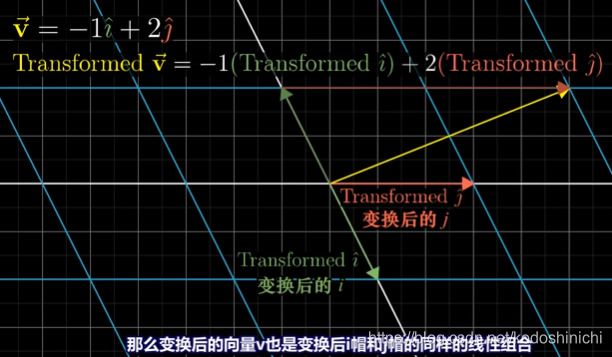
①之前在讲述向量的坐标表示时曾讲到过:向量就是基向量的一个线性组合
②无论在什么时候,这一观点都成立,那么变换后的向量也自然是变换后的基向量的线性组合
由上可知,值根据变换后的i与j两个基向量,就可以推断出变换后的向量v
2.线性变换结果的计算与求解
只要给定了一个变换方阵和初始向量,通过相关运算(后文会把该运算定义为矩阵乘法)得到变换后的向量表示
扫描二维码关注公众号,回复: 11596442 查看本文章
任意一个变换矩阵都可以看做是一个特殊符号,它表征了一个线性变换,按列取出向量与初始向量进行缩放和加法运算即可。
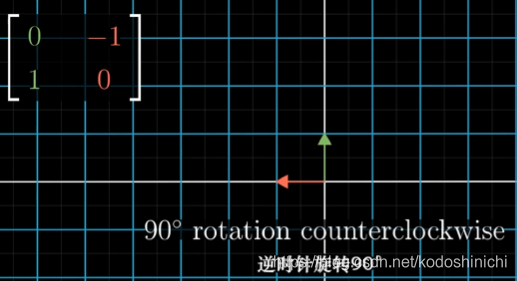
3.用矩阵表示一些特殊的线性变换——记住,变换矩阵(2x2:这里是二维的)每一列对应一个变换后的基向量
①逆时针旋转90°
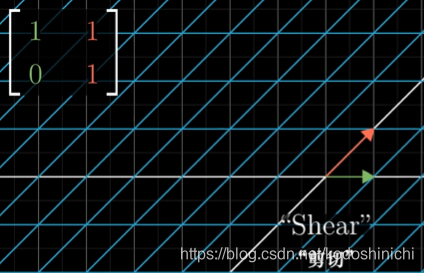
②剪切
复合变换与复合矩阵与矩阵乘法
- 复合变换可以看成相继使用若干线性变换
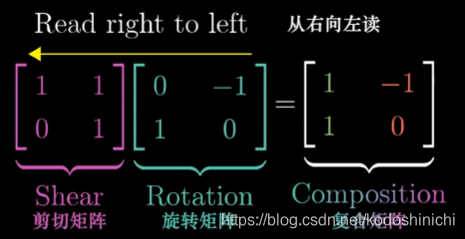
- 【从变换的角度来理解矩阵乘法】复合变换对应一个变换矩阵,该矩阵可以由若干个线性变换的变换矩阵左乘得到。

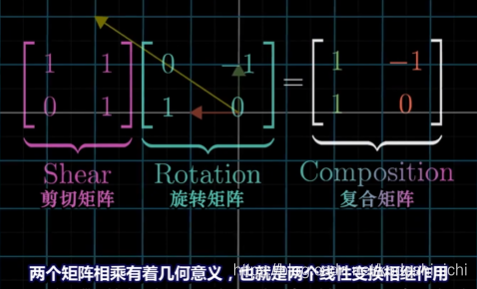
- 在上述复合变换的背景下,两个矩阵相乘也有了对应的几何意义,也就是两个矩阵对应的线性变换项集作用。
- 复合矩阵的顺序性
对多个矩阵进行复合,要先应用最靠近右侧的变换矩阵。
可以类比函数的记法与函数的复合,函数符号写在自变量左侧,所以函数复合时也是从右往左读
-
【从矩阵相乘的角度来理解变换】给定两个变换矩阵,通过使用矩阵乘法或者变换与矩阵对应的关系来求解。

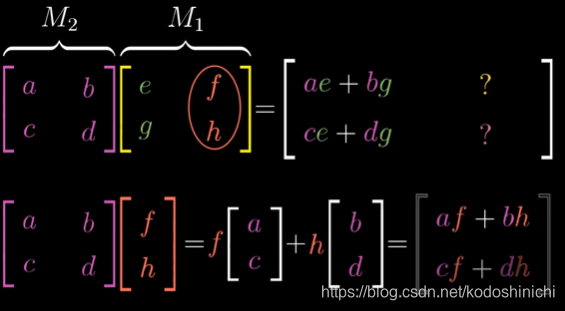
-
从而可以理解矩阵乘法的相关性质
①矩阵乘法一般不满足交换性——变换有顺序
②矩阵乘法满足结合性——本质就是将相同的几个变换按照既定的顺序依次进行而已
三维空间线性变换
- 三维空间本质上和二维线性变换没有相异处,只不过基向量从两个二维基向量变成了3个三维基向量。
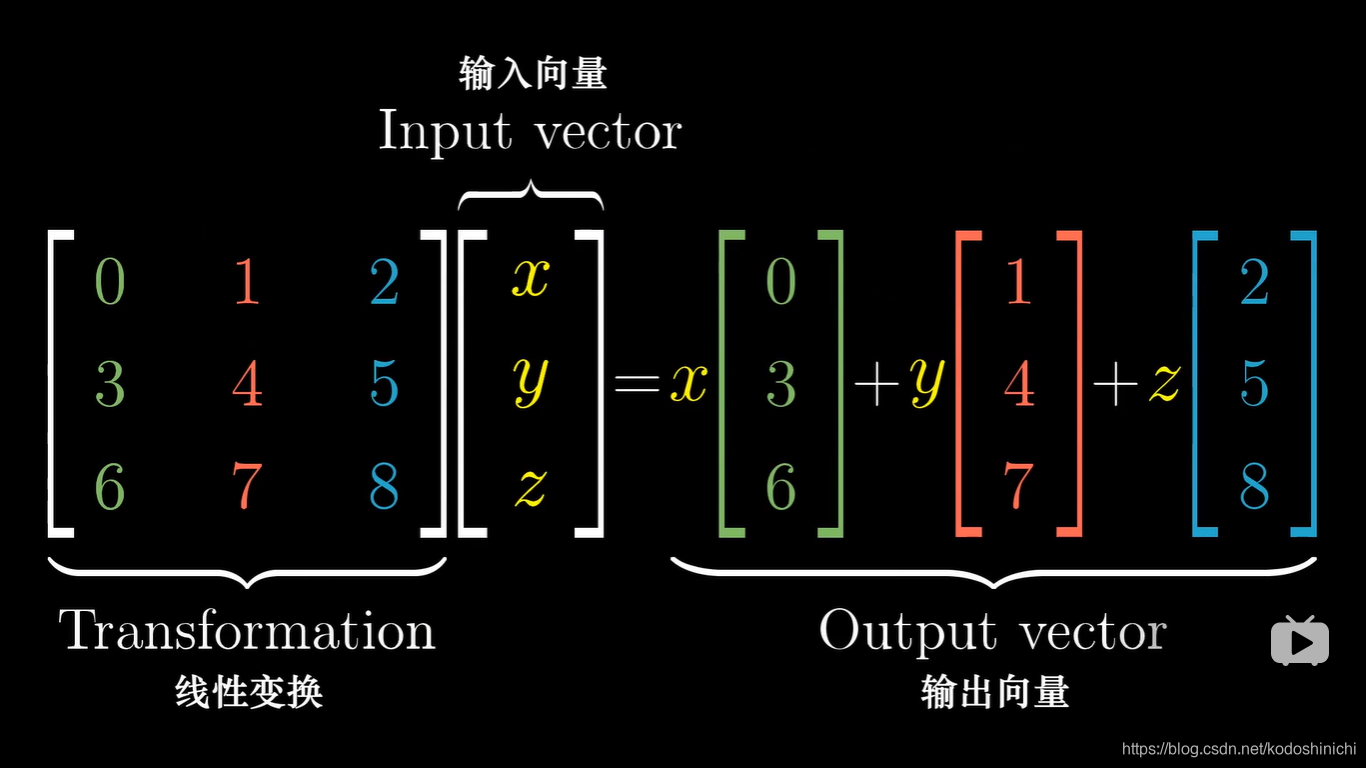
- 三维矩阵的乘法依然可以使用“依次作用的线性变换”来理解,且矩阵的乘法在三维空间旋转变换只能够经常用到。
原视频
【官方双语/合集】线性代数的本质 - 系列合集-04
【官方双语/合集】线性代数的本质 - 系列合集-05
【官方双语/合集】线性代数的本质 - 系列合集-06