【编译原理】DFA-NFA以及相关算法思想

1.词法分析概述.

DFA-NFA以及正规式、正规文法之间是等价的，它们都是用于描述词法规则的数学工具，我们在词法分析阶段，如何判定一个单词是否合法，就是借助这些工具。词法分析器的功能是输入源程序，输出单词符号。单词符号是一个程序语言的基本语法符号，程序语言的单词符号一般可以分为下列五种：

1. 关键字：是由程序语言定义的具有固定意义的标识符，有时候这些标识符作为保留字或基本字。例如C语言中的if、else、for、while等都是保留字，这些字通常不用作一般标识符；
2. 标识符：用来表示各种名字，如变量名、数组名、过程名等等；
3. 常数：常数的类型一般有整型，实型、布尔型、字符串型等，例如8、3.14、true、“编译原理太难了”等等；
4. 运算符：如+、-、*、/等等；
5. 界符：如逗号，分号、括号以及注释符号/* */等等。

2.正规式与有限自动机.

对于字母表Σ，我们感兴趣的是它的一些特殊字集，即所谓的正规集，我们使用正规式这个概念来表示正规集，其递归定义如下：

①ε和Φ都是Σ上的正规式，它们表示的正规集分别是{ε}和Φ；
②任何a∈Σ，a是Σ上的一个正规式，它所表示的正规集为{a}；
③假定U和V都是Σ上的正规式，它们所表示的正规集分别记为L(U)和L(V)，那么(U|V)、(UV)和(U)*都是正规式，它们所表示的正规集分别为L(U)∪L(V)、L(U)L(V)和(L(U))*.
仅有限次使用上述三个步骤得到的表达式才是Σ上的正规式，仅由这些正规式所表示的字集才是Σ上的正规集。

一个确定有限自动机(DFA)M是一个五元组：(S,Σ,δ,s $_0$,F)，其中：

• S是一个有限集，它的每一个元素称为一个状态；
• Σ是一个有穷字母表，它的每一个元素称为一个输入字符；
• δ是一个从S×Σ至S的单值部分映射。δ(s,a)=s $_1$意味着：当现行状态为s、输入字符为a时，将转换到下一个状态s $_1$，我们称s $_1$为s的一个后继状态；
• s $_0$∈S，是唯一的初态；
• F⊆S，是一个终态集(可空)，F为空的DFA对于任何输入串都不会终止，可以认为这个DFA不接受任何字符。

一个非确定有限自动机(NFA)M是一个五元组：(S,Σ,δ,S $_0$,F)，其中：

• S是一个有限集，它的每一个元素称为一个状态；
• Σ是一个有穷字母表，它的每一个元素称为一个输入字符；
• δ是一个从S×Σ至S的子集的映射，即δ：S×Σ→2^s；
• S $_0$⊆S，是一个非空的初态集合；
• F⊆S，是一个终态集(可空)。

显然，我们可以看出DFA是NFA的特例。对于每一个NFA M $_0$，我们都可以找到一个DFA M $_1$，使得L(M $_0$)=L(M $_1$)，证明过程在下一节给出。

3.DFA与NFAの等价性证明.

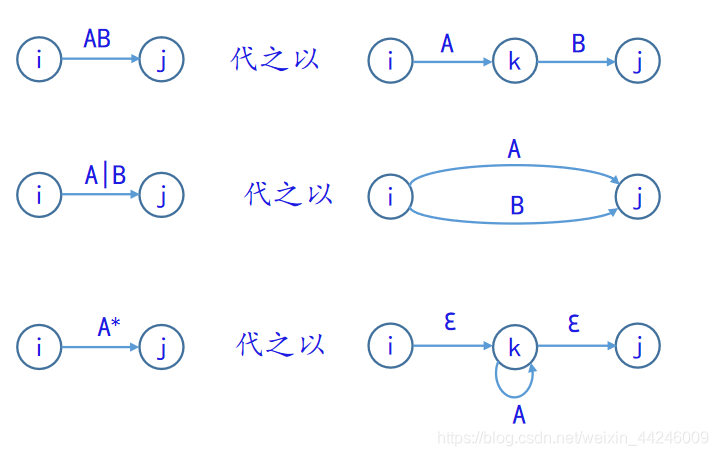
NFA与DFA的等价性证明是通过构造性算法——子集构造法(Subset Construction Algorithm)来完成的，构造性算法的意思是，对于任意一个给定的NFA，我们通过这一算法，都能够构造出一个与其等价的DFA。如此一来，我们不仅证明了NFA与DFA的等价性，也给出了求得这一等价DFA的方法。这一过程也叫做NFA的确定化，输入是非确定有限自动机NFA，输出是确定有限自动机DFA。下面给出证明DFA与NFA等价性的算法：


【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

4.正规文法与有限自动机の等价性证明.

对于一个正规文法G和有限自动机M，如果存在L(G)=L(M)，则称G和M是等价的。并且我们有以下结论：

• 对于每一个右线性正规文法G或左线性正规文法G，都存在一个FA M使得L(M)=L(G);
• 对于每一个FA M，都存在一个右线性正规文法G $_R$和左线性正规文法G $_L$，使得L(M)=L(G $_R$)=L(G $_L$).

下面我们给出这两条结论的证明：

1.结论1证明.

2.结论2证明.

5.正规式与有限自动机の等价性证明.

关于正规式和有限自动机，我们有如下两个结论：

• 对于任何FA M，都存猜一个正规式E，使得L(E)=L(M);
• 对于任何正规式E，都存在一个FA M，使得L(M)-L(E).

至此，我们得到的所有结论综合起来，说明正规式、正规文法以及有限自动机(DFA和NFA)在接收语言的能力上是互相等价的。

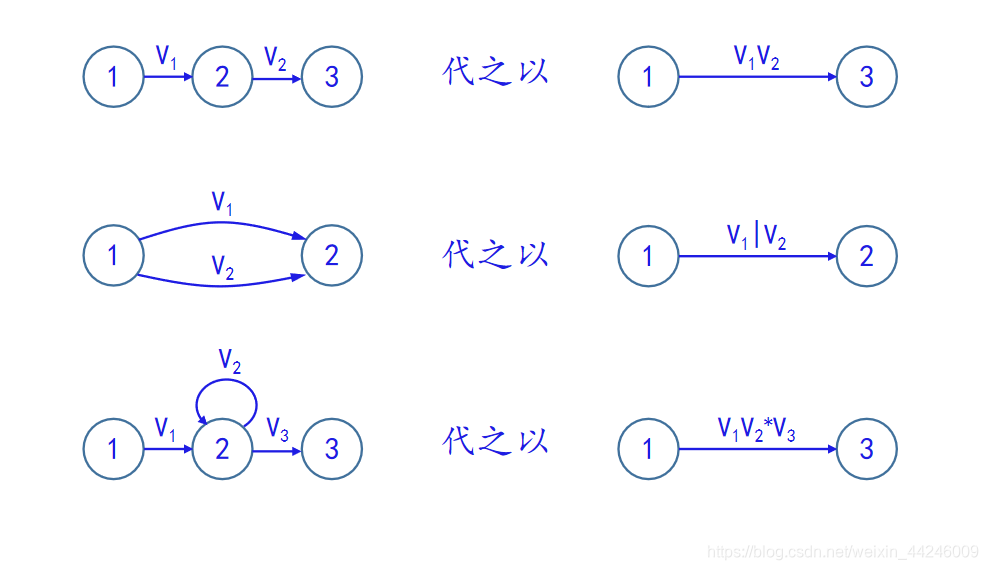
1.结论1证明.

其中消去结点的规则，如下图所示：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

6.DFAの最小化.

一个确定有限自动机M的化简是指寻找一个状态数比M少的DFA M $_1$，使得L(M)=L(M $_1$).Hopcroft算法就是这样的一个算法，我们输入一个严格定义的DFA M，算法输出的结果是一个拥有最小状态数的等价DFA M $_1$.
首先我们要给出DFA中状态等价的概念，假定s和t是DFA M中的两个状态，若从s出发读入某个字w而到达终态，则t也可以读入w而到达终态；并且若从t出发读入某个字w能够到达终态，则s也能读入w而到达终态，那么我们就称s和t是等价的状态。如果两个状态不等价，我们就说这两个状态是可以区别的，例如所有的终结态和非终结态之间就是可以区别的，因为终结态可以识别ε，而非终结态无法识别ε。
将DFA最小化的过程旨在将M的状态集合分割成一些不相交的子集，使得任意两个不同的子集中的状态之间都是可区别的，而同一子集中的任何两个状态都是等价的。最后，在每一个子集中选取一个代表，同时消去其他的等价状态。
对M的状态集S进行划分的步骤是：首先，把S的终态与非终态分开，形成一个基本划分Π，前面也说过，属于这两个子集的状态是必然可以区分的。假定到某个时候，Π已经包含m个子集，记Π={S¹,S²,…,S^m}，并且属于不同子集的状态是可以区别的。检查Π中的每个Sⁱ，看能否进一步划分。对于某一个Sⁱ，令Sⁱ={q $_1$,q $_2$,…,q $_k$}，若存在一个输入字符a使得Sⁱ $_a$不全包含在现时的Π的某一个子集中，就需要将Sⁱ一分为二。假定状态s $_1$和s $_2$经过a弧分别到达t $_1$和t $_2$状态，并且t $_1$和t $_2$分属于现时Π的两个状态子集，那就需要将Sⁱ一分为二，使得一半含有s $_1$:

另一半含有s $_2$:S^ib=Sⁱ-S^ia.
直到最后没有一个状态子集可以被进一步分割，就已经完成了DFA的最小化，这就是Hopcroft算法的思想。

7. 正规式→DFAの直接转换算法.

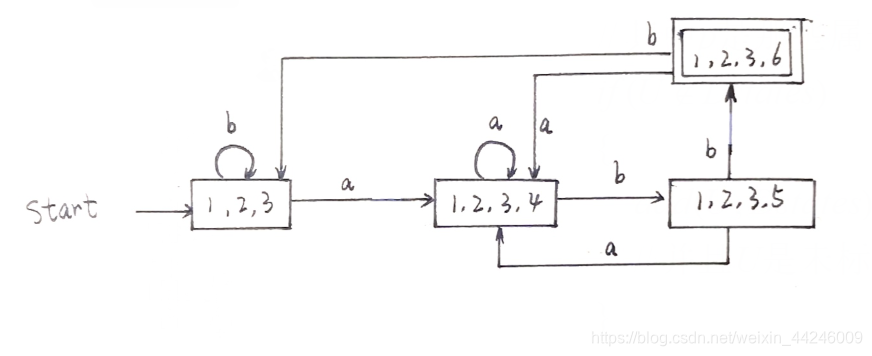
一般来说，对于一个给定的正规式，我们首先使用Thompson算法将其转换为一个NFA，再使用子集构造法将NFA转换为DFA，最后如果有需要，我们可以使用Hopcroft算法完成对该DFA的最小化。那这个部分，我们要介绍的就是一种，从正规式直接转换为DFA，一步到位的算法。虽然相比之下，这一算法比Thompson、子集构造以及Hopcroft算法中的任何一个都要复杂，但我们考察整个RE→DFA的过程，这一算法无疑比后三者的级联快得多。我们给出一个示例正规式:

(a|b)*abb

来叙述该算法的执行过程。

1.NFAの重要状态.

如果一个NFA状态有一个标号非ε的离开转换，那么我们称这个状态是重要状态。

其实我们在子集构造法中，计算I $_a$=ε_CLOSURE(J)时，其中J是集合I中状态经过一条a弧能够到达的状态的集合，也只是使用了集合I中的重要状态，大家可以后续自己进行验证。由于我们通过Thompson算法构造出的NFA只有一个接受状态，并且该接受状态因为没有离开转换，所以不是重要状态。对于这样的情况，我们可以在正则表达式R的右端，连接一个特殊的、用于标记结束的符号#，使得R对应的NFA的接受状态有一个标记为#的离开转换。也就是说，我们将R扩展为了R#，这一扩展使得我们在构造的过程中，可以不考虑接受状态原本不是重要状态的问题。当构造过程结束后，任何在#上有离开转换的状态，必然是一个接受状态。

2.REの抽象语法树.

NFA的重要状态直接对应于RE中存放了Σ中符号的位置，使用抽象语法树来表示扩展之后的RE是非常有用且直观的。该语法分析树的叶子结点对应于运算分量，而内部结点对应于运算符。标号为连接运算符o，并运算符|以及星闭包运算符*的内部结点分别称为cat结点、or结点和star结点。对于我们给出的示例正规式，从左到右进行扫描，构造出的抽象语法树如下，注意该正规式是已经经过扩展的，即(a|b)*abb#:

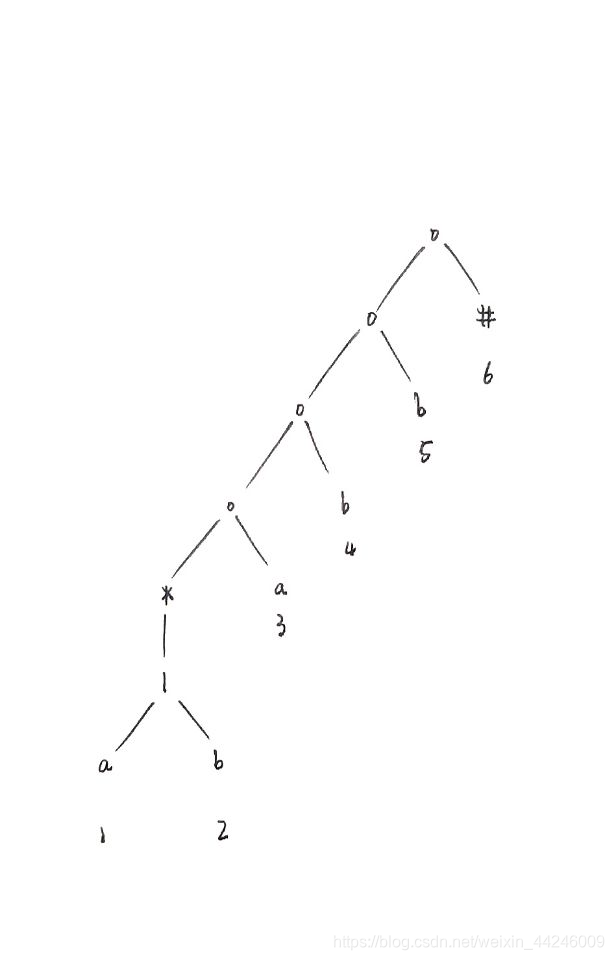
抽象语法树的图示中，我们为每一个叶子结点编号，这些编号对于我们后续的计算至关重要。

3.nullable、firstpos、lastpos、followpos.

1. nullable(n)对于一个抽象语法树的结点n来说，其值为真当且仅当结点n代表的子表达式的语言中包含空串ε，也就是说n结点代表的子表达式能够“生成空串ε”或者“其本身就是空串ε”；
2. firstpos(n)定义了以结点n为根的子树中的某些特定位置的集合，这些位置对应于以n为根的子表达式的语言中某个串的第一个符号；
3. lastpos(n)与firstpos(n)类似，只不过它的特殊位置对应于以n为根的子表达式的语言中某个串的最后一个符号；
4. followpos(n)的定义描述相当反人类，后续我们先给出具体的计算方法，再给出其严格的定义。

对于我们采用的示例RE(a|b)*abb#，其抽象语法树已经构建完成，下面我们进行上述四个函数对于每个结点的的计算。以(a|b)*为例，我们记该代表该子表达式的star结点为n，则有nullable(n)=true。对于firstpos(n)，我们看(a|b)*所能够产生的语言中，它的第一个字母，可能是抽象语法树中位置为1的a，也可能是位置为2的b，所以firstpos(n)={1,2}；lastpos(n)的计算也是类似，最末的一个字母同样可能是a，可能是b。为了加深概念的理解，我们再考察(a|b)*a这一子表达式，同样记该cat结点为n，显然n结点不可能推出ε，所以nullable(n)=false，对于firstpos(n)而言，它的起始字母，可能是位置1的a，可能是位置2的b，可能是位置3的a，所以firstpos(n)={1,2,3}；而lastpos(n)则只会是位置3的a，所以lastpos(n)={3}。下图中我们给出所有结点的firstpos以及lastpos的结果，结点左边的是firstpos集合，右边的是lastpos集合。

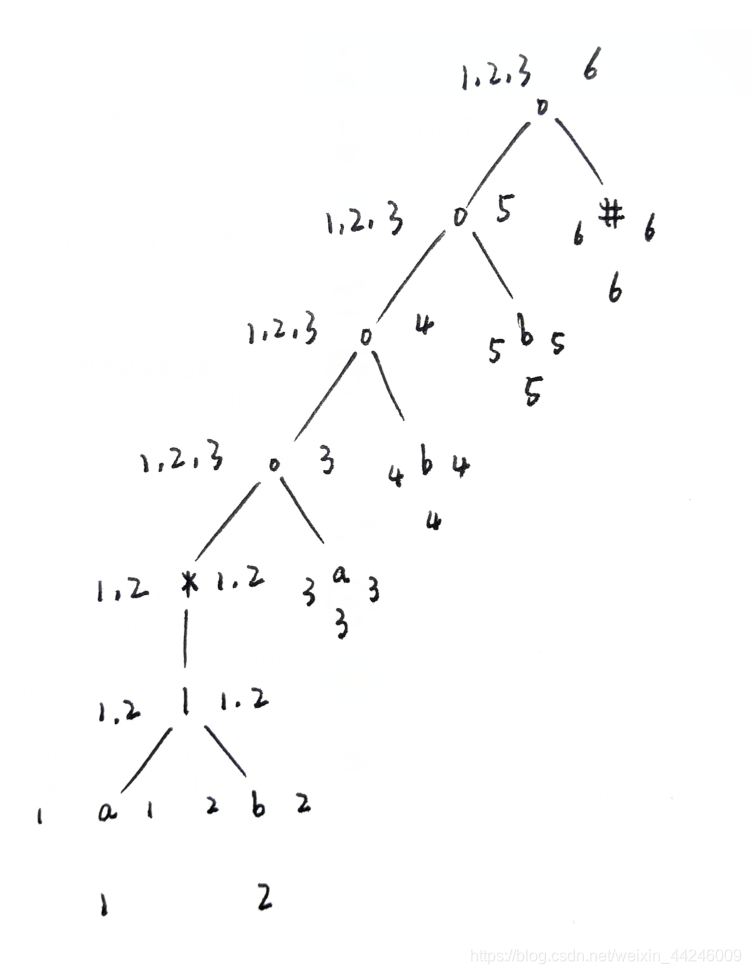
最后，最为重要的followpos集合的计算规则：

1. 如果n是一个cat结点，我们记其左右结点为Left和Right，那么对于lastpos(Left)中的任意一个位置i而言，firstpos(Right)都在followpos(i)中；
2. 如果n是一个star结点，i是lastpos(n)中的任意一个位置，那么firstpos(n)中的每一个位置j都在followpos(i)中。

至此，我们可以给出followpos的定义：

followpos(i)定义了一个和位置i相关的、抽象语法树中的某些位置的集合。位置j在followpos(i)中当且仅当存在L(R#)中的某个串w=a $_1$a $_2$…a $_n$，使得我们在解释为什么w属于L(R#)时，可以将w中的某个a $_s$和抽象语法树中的位置i对应，而a $_{s+1}$和抽象语法树中的位置j对应。

下图中，我们给出示例RE(a|b)*abb#的followpos集合的结果：

我们选取几个位置来叙述一下，followpos的计算过程。首先，针对抽象语法树中的star结点n，我们需要将firstpos(n)中的所有位置都加入到lastpos(n)的任意一个位置i的followpos(i)中，对应于规则2，所以followpos(1)中会有{1,2}，followpos(2)也是如此。对于表示(a|b)*a的cat结点n，我们需要将firstpos(Right)添加到lastpos(Left)中的任意一个位置i的followpos(i)中，所以followpos(1)中会有{3}，followpos(2)也是如此，所以最终followpos(1)={1,2,3}.

4.构造DFA算法.

至此我们已经完成了抽象语法树的构造，以及nullable、firstpos、lastpos和followpos的计算，下一步就可以开始构造DFA了，也就是构造DFA的状态集合Dstates以及迁移函数Dtran。DFA的状态就是抽象语法树T中的位置集合，每一个状态初始都是“未标记的”，当我们开始考虑这一状态的离开转换时，将其设置为“已标记的”。DFA的开始状态是firstpos(root)，root代表抽象语法树的根结点，DFA的终结状态是那些包含了#所在位置的状态。下面我们给出构造算法的伪代码描述：

最终生成的DFA如下所示：