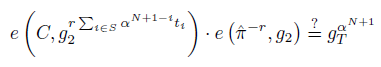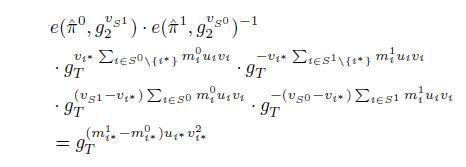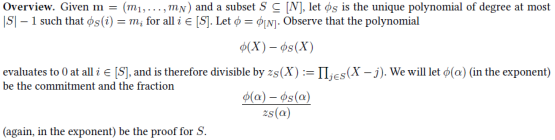Pointproofs: Aggregating Proofs for Multiple Vector Commitments 学习笔记2

1. 引言

在博客 Pointproofs: Aggregating Proofs for Multiple Vector Commitments 学习笔记1中，主要对 Algorand团队Gorbunov等人2020年论文《Pointproofs: Aggregating Proofs for Multiple Vector Commitments》做了一个总体的梳理。该论文在 Libert和Yung 2010年论文《Concise mercurial vector commitments and independent zero-knowledge sets with short proofs》的基础上，做了以下改进：

• 采用了非对称bilinear pairing group，并针对 $\mathbb{G}_1$域内的运算效率> $\mathbb{G}_2$> $\mathbb{G}_T$，对Verify算法做了优化（计算 $r=(\sum_{i\in S}m_it_i)^{-1}\ mod\ p$，将 $\mathbb{G}_T$域内的运算转移到 $\mathbb{G}_1$域内）：
  
• 采用Random Oracle Model，基于hash函数 $H$引入了随机参数 $t_i=H(i,C,S,\vec{m}[S])$来实现same-commitment aggregation；基于hash函数 $H$和 $H'$引入了随机参数 $t_{j,i}=H(i,C_j,S_j,\vec{m}_j[S_j])$和 $t_j'=H'(j,\{C_j,S_j,\vec{m}_j[S_j]\}_{j\in[l]})$来实现cross-commitment aggregation。

本博客将重点关注：

• proof of correctness/binding for same-commitment aggregation
• proof of correctness/binding for cross-commitment aggregation
• same-commitment aggregation from CDH-like assumption
• weak binding and realization
• cross-commitment aggregation from polynomial commitments
• https://github.com/algorand/pointproofs 代码解析

该论文实现的binding属性是基于AGW+ROM model under the $l$-wBDHE assumption：（详细定义参见博客 Pointproofs: Aggregating Proofs for Multiple Vector Commitments 学习笔记1 1.1节内容）

2. proof of correctness/binding for same-commitment aggregation

2.1 same commitment aggregation

具体的实现为：

• Setup( $1^{\lambda},1^N$)：取随机值 $\alpha\leftarrow \mathbb{Z}_p$，输出：【其中 $\vec{a}=(\alpha,\alpha^2,\cdots,\alpha^N)$】
  $g_1^{\vec{a}}=(g_1^\alpha,\cdots,g_1^{\alpha^N})$
  $g_1^{\alpha^N\vec{a}[-1]}=(g_1^{\alpha^{N+2}},\cdots,g_1^{\alpha^{2N}})$
  $g_2^{\vec{a}}=(g_2^\alpha,\cdots,g_2^{\alpha^N})$
  $g_T^{\alpha^{N+1}}=e(g_1^{\alpha},g_2^{\alpha^N})$
  Prove key为： $g_1^{\vec{a}}，g_1^{\alpha^N\vec{a}[-1]}$
  Verify key为： $g_2^{\vec{a}},g_T^{\alpha^{N+1}}$
  而 $\alpha$为有毒垃圾，trusted setup后应直接丢弃，must never be known to the adversary。

• Commit( $\vec{m}$) for $\vec{m}\in \mathbb{Z}_p^N$：
  $C=g_1^{\vec{m}^T\vec{a}}=g_1^{\sum_{i\in N}m_i\alpha^i}$

• UpdateCommit( $C,S,\vec{m}[S],\vec{m}'[S]$)：
  $C'=C\cdot g_1^{(\vec{m}'[S]-\vec{m}[S])^T\vec{a}[S]}=C\cdot g_1^{\sum_{i\in S}(m_i'-m_i)\alpha^i}$

• Prove( $i,\vec{m}$)：open第 $i$个位置。
  $\pi_i=g_1^{\alpha^{N+1-i}\vec{m}[-i]^T\vec{a}[-i]}=g_1^{\sum_{j\in [N]-\{i\}}m_j\alpha^{N+1-i+j}}$
  其中 $g_1^{\alpha^{N+1-i}\vec{a}[-i]}$均已包含在了Prove key中了。
  若 $m_j$ at index $j\neq i$ changes to $m_j'$，则 $\pi_i'=\pi\cdot g_1^{(m_j'-m_j)\alpha^{N+1-i+j}}$，若 $m_i$ changes to $m_i'$，则proof 不变 $\pi_i'=\pi_i$。但是两种情况下，commitment $C$均需要更新为 $C'$。

• Aggregate( $C,S,\vec{m}[S],\{\pi_i:i\in S\}$)：
  $\hat{\pi}=\prod_{i\in S}\pi_i^{t_i}$
  其中 $t_i=H(i,C,S,\vec{m}[S])$

• Verify( $C,S,\vec{m}[S],\hat{\pi}$)：
  验证 $e(C,g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}$ 是否成立。
  其中 $t_i=H(i,C,S,\vec{m}[S])$

2.2 proof of correctness for same-commitment aggregation

对于任意的 $i\in [N],\pi_i=Prove(i,\vec{m})=g_1^{\alpha^{N+1-i}\vec{m}[-i]^T\vec{a}[-i]}$，对Commit/Prove/Aggregate/Verify整个流程，可分两步证明：

• 1）证明 $e(C,g_2^{\alpha^{N+1-i}})=e(\pi_i,g_2)\cdot g_T^{\alpha^{N+1}m_i}$
• 2）证明 $e(C,g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}$

具体为：
1）有 $\vec{m}^T\vec{a}=\vec{m}[-i]^T\vec{a}[-i]+\alpha^im_i$
等式左右两边同时乘以 $\alpha^{N+1-i}$，有：
$(\vec{m}^T\vec{a})\alpha^{N+1-i}=\alpha^{N+1-i}\vec{m}[-i]^T\vec{a}[-i]+\alpha^{N+1}m_i$
转换为pairing计算，有：
$e(g_1^{\vec{m}^T\vec{a}},g_2^{\alpha^{N+1-i}})=e(g_1^{\alpha^{N+1-i}\vec{m}[-i]^T\vec{a}[-i]},g_2)\cdot g_T^{\alpha^{N+1}m_i}$
从而证明了 $e(C,g_2^{\alpha^{N+1-i}})=e(\pi_i,g_2)\cdot g_T^{\alpha^{N+1}m_i}$ 成立。

2）在 $e(C,g_2^{\alpha^{N+1-i}})=e(\pi_i,g_2)\cdot g_T^{\alpha^{N+1}m_i}$的基础上，等式左右两侧均进行 $t_i$次幂乘，则有：
$e(C,g_2^{\alpha^{N+1-i}t_i})=e(\pi_i^{t_i},g_2)\cdot g_T^{\alpha^{N+1}m_it_i}$
将要open的 $S$集合内的所有公式均乘一块，有（for all $i\in S$）：
$e(C,g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\prod_{i\in S}\pi_i^{t_i},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}$ 成立。

证明UpdateCommit算法正确性的思路为：
$\vec{m}'^T\vec{a}=(\vec{m}'[S]-\vec{m}[S])^T\vec{a}[S]+\vec{m}^T\vec{a}$ 等式恒成立。

2.3 proof of binding for same-commitment aggregation

采用归谬法来证明，假设adversary 可计算 $C=g_1^{\vec{z}^T\vec{a}}$，并为 $(S,\vec{m}[S])$提供proof $\hat{\pi}$【其中 $\vec{m}[S]\neq \vec{z}[S]$】，使得 $\hat{\pi}$可被Verify通过。
$e(g_1^{\vec{z}^T\vec{a}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}z_it_i}=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}$

注意adversary也不知道 $g_1^{\alpha^{N+1}}$，即 $\log_{g_1}\hat{\pi}$ 中 $\alpha^{N+1}$ 项的系数应为 $0$。
比较上述等式中 $g_T^{\alpha^{N+1}}$的系数应满足：
$\sum_{i\in S}m_it_i\equiv_p \sum_{i \in S}z_it_i$
用向量表示，应满足：
$\vec{z}[S]^T\vec{t}\equiv_p \vec{m}[S]^T\vec{t}$
其中 $\vec{t}=(H(i,C,S,\vec{m}[S]),i\in S)$

假设当 $(S,\vec{z}[S],\vec{m}[S])$确定后， $\vec{t}\leftarrow \mathbb{Z}_p^{|S|}$为chosen uniformly at random 时，则有：
$\Pr_{\vec{t}}[\vec{z}[S]\not\equiv_p \vec{m}[S]\ and\ \vec{z}[S]^T\vec{t}\equiv_p \vec{m}[S]^T\vec{t}]=1/p$
即相应的概率可忽略。

因此问题的关键在于：ensure the uniform choice of $\vec{t}$ for any fixed $(S,\vec{z}[S],\vec{m}[S])$。
注意有：

• $C$ determines $\vec{z}$ in AGM；
• $C,S,\vec{m}[S]$为random oracle $H(i,\cdot,\cdot,\cdot)$ 的input，输出为 $t_i$。

若adversary可以找到相应的 $m_i\neq z_i$值，使得：
$\sum_{i\in S}z_it_i\equiv_p \sum_{i \in S}m_it_i$
成立，则binding属性不成立。

2.3.1 为何需要将 $C,S,\vec{m}[S]$作为 $H$的input？

$t_i=H(i,\cdot,\cdot,\cdot)$，为什么需要将 $C,S,\vec{m}[S]$作为 $H$的input？

• 若 $t_i$与 $m_i$无关，则adversary可指定 $|S|-1$个 $m_i$的值，并根据 $\sum_{i\in S}z_it_i\equiv_p \sum_{i \in S}m_it_i$等式计算最后一个 $m_i$的值。从而破坏了binding属性。
• 若 $t_i=H(i,C)$，Wanger’s attack可产生a $2^{\sqrt{\log p}}$ algorithm that given $\{z_it_i,m_it_i\}_{i \in [N]}$，从而计算a set $S$ of size $2^{\sqrt{\log p}}$ 使得 $\sum_{i\in S}z_it_i\equiv_p \sum_{i \in S}m_it_i$ 等式成立。对于128-bit security level for the curve(如 $\log p\approx 256$)， $2^{\sqrt{\log p}}\approx 2^{16}$，which makes for a very pratical attack。
• 若 $t_i=H(i,C,S)$，可能存在与 $t_i=H(i,C)$类似的攻击。【It seems plausible that the attack also extends to the setting of $t_i = H(i, C, S)$: it would suffice to extend Wagner’s algorithm to finding values that sum to a given constant, because the values of the elements of S are not committed, and thus, although $\sum_{i\in S} z_it_i$ is fixed, the attacker can choose from a list of random $m_i$ for each $i \in S$.】

2.3.2 binding for same-commitment aggregation 分析

分为两步来分析：
1）bounding “lucky” queries。
相当于对于固定 $C,S,\vec{m}[S]$，寻找符合要求的 $\vec{z}和\vec{y}$，满足 $C=g_1^{\vec{z}^T\vec{a}+\alpha^N\vec{y}^T\vec{a}[-1]}$，同时满足 $\vec{m}[S]\not\equiv_p\vec{z}[S]且(\vec{m}[S]-\vec{z}[S])^T\vec{t}\equiv_p 0$。若能找到相应的 $\vec{z}和\vec{y}$，则称为“H-lucky”。

正常open为 $\{z_i\}_{i\in [S]}$的话，则 $e(C,g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(g_1^{\vec{z}^T\vec{a}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}z_it_i}$ 等式是恒成立的。若想作弊open为 $\{m_i\}_{i\in [S]}，其中\vec{m}[S]\neq \vec{z}[S]$的话，则在等式两边都乘以 $e(g_1^{\sum_{j\in[N-1]}y_j\alpha^{N+1+j}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})$的话，则有：

• 等式左边为： $e(g_1^{\vec{z}^T\vec{a}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})\cdot e(g_1^{\sum_{j\in[N-1]}y_j\alpha^{N+1+j}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(g_1^{\sum_{i\in[N]}z_i\alpha^i+\sum_{j\in[N-1]}y_j\alpha^{N+1+j}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(C',g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})$

• 等式右边为： $e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}z_it_i}\cdot e(g_1^{\sum_{j\in[N-1]}y_j\alpha^{N+1+j}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}z_it_i}\cdot e(g_1,g_2)^{\alpha^{N+1}\sum_{j\in[N-1]}y_j\alpha^j\cdot\sum_{i\in[S]}\alpha^{N+1-i}t_i}$
  其中 $\sum_{j\in[N-1]}y_j\alpha^j\cdot\sum_{i\in[S]}\alpha^{N+1-i}t_i=\sum_{i\in [S]}(t_i\cdot \sum_{j\in[N-1]}y_j\alpha^{N+1-i+j})=\sum_{i\in[S]}t_ix_i$， $x_i=\sum_{j\in[N-1]}y_j\alpha^{N+1-i+j}$。

这样就有 $e(C',g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}z_it_i}\cdot g_T^{\alpha^{N+1}\sum_{i\in[S]}t_ix_i}=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}(z_i+x_i)t_i}=e(\hat{\pi},g_2)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}$
其中：
$m_i=z_i+x_i=z_i+\sum_{j\in[N-1]}y_j\alpha^{N+1-i+j}$
$C'=g_1^{\sum_{i\in[N]}z_i\alpha^i+\sum_{j\in[N-1]}y_j\alpha^{N+1+j}}$
$C=g_1^{\sum_{i\in[N]}z_i\alpha^i}$

也就是说，若adversary可找到相应的 $C'$，使得 $H(i,C,S,\vec{m}[S])=H(i,C',S,\vec{m}[S])$成立且 $C'=g_1^{\sum_{i\in[N]}z_i\alpha^i+\sum_{j\in[N-1]}y_j\alpha^{N+1+j}}且C=g_1^{\sum_{i\in[N]}z_i\alpha^i}$，则可作弊成功。即：
$e(C,g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})=(e(\hat{\pi},g_2)/e(g_1^{\sum_{j\in[N-1]}y_j\alpha^{N+1+j}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i}))\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}=e(g_1,\hat{\pi}^*)\cdot g_T^{\alpha^{N+1}\sum_{i\in S}m_it_i}$
其中 $e(g_1^{\sum_{j\in[N-1]}y_j\alpha^{N+1+j}},g_2^{\sum_{i\in S}\alpha^{N+1-i}t_i})$ 可根据现有的public parameter计算出来。 【这段话理解有问题，不应在于Hash碰撞，而在于，应该是对于固定 $C,S,\vec{m}[S]$，寻找符合要求的 $\vec{z}和\vec{y}$，满足 $C=g_1^{\vec{z}^T\vec{a}+\alpha^N\vec{y}^T\vec{a}[-1]}$，同时满足 $\vec{m}[S]\not\equiv_p\vec{z}[S]且(\vec{m}[S]-\vec{z}[S])^T\vec{t}\equiv_p 0$。若能找到相应的 $\vec{z}和\vec{y}$，则称为“H-lucky”。】
从而，对于 $C$，adversary可通过提供proof $\hat{\pi}^*$ 作弊成功——将本应为 $\vec{z}[S]$ open 为了 $\vec{m}[S]$。

由于 $\Pr_{\vec{t}}[\vec{z}[S]\not\equiv_p \vec{m}[S]\ and\ \vec{z}[S]^T\vec{t}\equiv_p \vec{m}[S]^T\vec{t}]=1/p，其中\vec{t}=(H(i,C,S,\vec{m}[S]):i\in S)$，也就是说，对于固定的 $(S,\vec{m}[S],\vec{z}[S])$，找到相应的 $C'$使得 $H(i,C,S,\vec{m}[S])=H(i,C',S,\vec{m}[S])$成立，且存在 $\vec{z}\in \mathbb{Z}_p^N,\vec{y}\in\mathbb{Z}_p^{N-1}$使得 $C'=g_1^{\sum_{i\in[N]}z_i\alpha^i+\sum_{j\in[N-1]}y_j\alpha^{N+1+j}}，C=g_1^{\sum_{i\in[N]}z_i\alpha^i}$的概率不高于 $1/p$。

By the union bound, the probability that an adversary makes an H-lucky query is at most $q_H/p$, where $q_H$ is the number of queries to $H$. Below, we assume this never happens。

2）若可extracting $g_1^{\alpha^{N+1}}$，则可破坏本论文 $l$-wBDHE security assumption。

若对于 $C=g_1^{\vec{z}^T\vec{a}+\alpha^N\vec{y}^T\vec{a}[-1]}=g_1^{\sum_{i\in[N]}z_i\alpha^i+\sum_{j\in[N-1]}y_j\alpha^{N+1+j}}$，存在 $(S^*,\vec{m}^*,\hat{\pi}^*)$ 使得：
$\vec{m}^*[S^*]\neq \vec{z}[S^*] 且 Verify(C,S^*,\vec{m}^*[S^*],\hat{\pi}^*)$ 成立。

即有 $e(C,g_2^{\sum_{i\in S^*}\alpha^{N+1-i}t_i})=e(\hat{\pi}^*,g_2)\cdot g_T^{\alpha^{N+1}\vec{m}^*[S^*]^T\vec{t}}$成立，其中 $t_i=H(i,C,S^*,\vec{m}^*[S^*])$。

于是有： $C^{\sum_{i\in S^*}\alpha^{N+1-i}t_i}=\hat{\pi}^*\cdot g_1^{\alpha^{N+1}\vec{m}^*[S^*]^T\vec{t}}$ 成立。

上述等式左侧展开为含 $g_1^{\alpha^{N+1}}$的项和不含 $g_1^{\alpha^{N+1}}$的项表示：
$C^{\sum_{i\in S^*}\alpha^{N+1-i}t_i}=g_1^{(\vec{z}^T\vec{a}+\alpha^N\vec{y}^T\vec{a}[-1])\cdot \sum_{i\in S^*}\alpha^{N+1-i}t_i}$

The smallest $i$ value is $1$.

(1)
$\vec{z}^T\vec{a}\sum_{i\in S^*}\alpha^{N+1-i}t_i=\sum_{i\in S^*}\vec{z}^T\vec{a}\alpha^{N+1-i}t_i =\sum_{i\in S^*}(z_i\alpha^i+\vec{z}[-i]\vec{a}[-i])\alpha^{N+1-i}t_i=\alpha^{N+1}\sum_{i\in S^*}z_it_i+\sum_{i\in S^*}\alpha^{N+1-i}\vec{z}[-i]\vec{a}[-i]t_i$

其中 $\sum_{i\in S^*}\alpha^{N+1-i}\vec{z}[-i]\vec{a}[-i]t_i$ depends on $g_1^{\alpha},g_1^{\alpha^2},\cdots,g_1^{\alpha^N},g_1^{\alpha^{N+2}},\cdots,g_1^{\alpha^{2N}}$。

(2)
$\alpha^N\vec{y}^T\vec{a}[-1])\cdot \sum_{i\in S^*}\alpha^{N+1-i}t_i$ depends on $g_1^{\alpha^{N+3}},\cdots,g_1^{\alpha^{3N}}$.

For :
$C^{\sum_{i\in S^*}\alpha^{N+1-i}t_i}=\hat{\pi}^*\cdot g_1^{\alpha^{N+1}\vec{m}^*[S^*]^T\vec{t}}$

Then:
$(g_1^{\sum_{i\in S^*,j\in S^*,i\neq j}z_jt_i\alpha^{N+1-i+j}})\cdot(g_1^{\vec{z}[-S^*]^T\vec{a}[-S^*]\cdot{\sum_{i\in S^*}\alpha^{N+1-i}t_i}})\cdot(g_1^{\alpha^N\vec{y}^T\vec{a}[-1])\cdot \sum_{i\in S^*}\alpha^{N+1-i}t_i})\cdot (\hat{\pi}^*)^{-1}=g_1^{\alpha^{N+1}\sum_{i \in S^*}(m_i-z_i)t_i}$ …<1>

当不存在H-lucky queries，且adversary可成功将 $\vec{z}[S^*]$ open 为不同的 $\vec{m}[S^*]$，则该adversary亦可根据上述公式成功计算等式右侧的 $g_1^{\alpha^{N+1}}$值。
因为：
$\vec{z}[S^*]\neq \vec{m}[S^*]$
所以：
$\sum_{i \in S^*}(m_i-z_i)t_i\not\equiv_p 0$
令：
$r=1/(\sum_{i \in S^*}(m_i-z_i)t_i)\mod p$
公式<1>左右两侧同时进行 $r$幂乘即可求得 $g_1^{\alpha^{N+1}}$值。

$\Rightarrow$ The winning algebraic adversary can be used to compute $g_1^{\alpha^{N+1}}$, CONTRADICTING $l$-wBDHE.

3. proof of correctness/binding for cross-commitment aggregation

3.1 cross commitment aggregation

Aggregation of proofs across $l$ commitments，在2.1 same commitment aggregation算法的基础上，增加了AggregateAcross和VerifyAcross算法，具体的实现为：

• AggregateAcross( $\{C_j,S_j,\vec{m}_j[S_j],\hat{\pi}_j\}_{j\in [l]}$)：
  $\pi=\prod_{j=1}^{l}\hat{\pi}_j^{t_j'}$
  其中：
  $t_j’=H’(j,\{C_j,S_j,\vec{m}_j[S_j]\}_{j\in[l]})$

• VerifyAcross( $\{C_j,S_j,\vec{m}_j\}_{j\in[l]},\pi$)：
  验证 $\prod_{j=1}^{l}e(C_j,g_2^{\sum_{i\in S_j}\alpha^{N+1-i}t_{j,i}})^{t_j'}=e(\pi,g_2)\cdot g_T^{\alpha^{N+1}\sum_{j\in[l],i\in S_j}m_{j,i}t_{j,i}t_j'}$ 等式是否成立。
  其中：
  $t_{j,i}=H(i,C_j,S_j,\vec{m}_j[S_j])$
  $t_j'=H'(j,\{C_j,S_j,\vec{m}_j[S_j]\}_{j\in[l]})$
  $\vec{m}_j=(m_{j,1},\cdots,m_{j,N})$

3.2 proof of correctness for cross-commitment aggregation

采用2.2类似的方式，证明 $\hat{\pi}_j$的正确性——each $\hat{\pi}_j$ satisfies its verification equation，然后raising $j$th verification equation to $t_j'$ and multiplying over all $j\in[l]$ yields the desired equality。

3.3 proof of binding for cross-commitment aggregation

分三步实现：
1）bounding “H-lucky” queries：
相当于对于固定 $C,S,\vec{m}[S]$，寻找符合要求的 $\vec{z}和\vec{y}$，满足 $C=g_1^{\vec{z}^T\vec{a}+\alpha^N\vec{y}^T\vec{a}[-1]}$，同时满足 $\vec{m}[S]\not\equiv_p\vec{z}[S]且(\vec{m}[S]-\vec{z}[S])^T\vec{t}\equiv_p 0$。若能找到相应的 $\vec{z}和\vec{y}$，则称为“H-lucky”。
采用与2.3.2 节第一步类似的方式，对于固定的 $(S,\vec{m}[S],\vec{z}[S])$，证明存在不同 $\vec{m}[S]\equiv_p \vec{z}[S]$，使得 $(\vec{m}[S]-\vec{z}[S])^T\vec{t}\equiv_p 0$的概率不高于 $1/p$。

2）bounding “H’-lucky” queries：
在 $l$ cross-commitment中，对于固定的 $\{(S_j,\vec{m}_j[S_j],\vec{z}_j[S_j])_{j\in[l]}\}$，存在任意一个 $\exists j: (\vec{m}_j[S_j]-\vec{z}_j[S_j])^T\vec{t}_j\not\equiv_p 0$，使得 $\sum_{j=1}^{l}(\vec{m}_j[S_j]-\vec{z}_j[S_j])^T\vec{t}_jt_j’\equiv_p 0$的概率不高于 $1/p$。

3）extracting $g_1^{\alpha^{N+1}}$：
当 $l=1$时，设置 $t_1’=1$，只验证Verify算法即可，extracting $g_1^{\alpha^{N+1}}$论证参见2.3.2节第二步。
若adversary 可成功将 $l$ commitments中的某一个open为 $\vec{m}_{j^*}^*[S_{j^*}^*]$而不是 $\vec{z}_{j^*}^*[S_{j^*}^*]$，并使得VerifyAcross算法验证通过，基本思路与2.3.2节第二步类似。
不存在H-lucky queries，则有：
$(\vec{m}_{j^*}^*[S_{j^*}^*]-\vec{z}_{j^*}^*[S_{j^*}^*])^T\vec{t}_{j*}\not\equiv_p 0$
不存在 H‘-lucky queries，则有：
$\sum_{h=1}^{l^*}(\vec{m}_j^*[S_j^*]-\vec{z}_j^*[S_j^*])^T\vec{t}_jt_j’\not\equiv_p 0$

则该adversary可采用2.3.2节第二步类似的方式计算出相应的 $g_1^{\alpha^{N+1}}$，从而破坏了 $l$-wBDHE的安全假设。

4. 基于CDH-like assumption构建的same-commitment aggregation

采用Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》类似思路（可参见博客Vector Commitments and their Applications学习笔记 第2.1节“基于CDH的Vector Commitment实现”内容）以及 Russell W. F. Lai 和 Giulio Malavolta 在Crypto 2019上发表的论文《Subvector Commitments with Application to Succinct Arguments》（参见博客 subvector commitment based on CubeDH assumption over pairing group 第4节“”内容），本文使用的是非对称pairing bilinear group。

采用CDH assumption，所需要的public parameter size为 $O(N^2)$。

在非对称pairing bilinear group中，本文用到的CDH-like static assumption为：
已知 $\{g_1^{u_i},g_2^{v_i}\}_{i\in [N]},\{g_1^{u_jv_i}\}_{i\neq j}$，计算 $g_T^{u_iv_i^2}$很难。

具体的实现为：

• Setup( $1^{\lambda},1^N$)：选择 $N$个随机数 $u_i,v_i\leftarrow \mathbb{Z}_p$，输出：
  $\{g_1^{u_i},g_2^{v_i}\}_{i\in [N]},\{g_1^{u_jv_i}\}_{i\neq j}$

• Commit( $\vec{m}$)：输出：
  $C=g_1^{\sum_{i\in[N]}m_iu_i}$

• UpdateCommit( $C,S,\vec{m}[S],\vec{m}’[S]$)：输出：
  $C’=C\cdot g_1^{\sum_{i\in S}(m_i’-m_i)u_i}$

• Prove( $i,\vec{m}$)：输出：
  $\pi_i=g_1^{\sum_{j\neq i}m_ju_jv_i}$

• Aggregate( $C,S,\vec{m}[S],\{\pi_i:i\in S\}$)：输出：
  $\hat{\pi}=\prod_{i\in S}\pi_i$

• Verify( $C,S,\vec{m}[S],\hat{\pi}$)：验证
  $e(C,g_2^{\sum_{i\in S}v_i})=e(\hat{\pi},g_2)\cdot g_T^{\sum_{i\in S}m_iu_iv_i}$ 等式是否成立。

注意：
在Russell W. F. Lai 和 Giulio Malavolta 在Crypto 2019上发表的论文《Subvector Commitments with Application to Succinct Arguments》（参见博客 subvector commitment based on CubeDH assumption over pairing group 第4节“”内容）中，所采用的是 $u_i=v_i$，在本论文中无法实现。【We do not know how to support aggregation in LM-CDH (which corresponds to the special case $u_i=v_i$).】

4.1 proof of correctness for same-commitment aggregation based on CDH-like assumption

verify公式为： $e(C,g_2^{\sum_{i\in S}v_i})=e(\hat{\pi},g_2)\cdot g_T^{\sum_{i\in S}m_iu_iv_i}$
直观地，有：
$(\sum_{j\in[N]}m_ju_j)\cdot v_i=m_iu_iv_i+\sum_{j\neq i}m_ju_jv_i$
从而open单个位置verify成功。
对所有的位置 $i\in S$，将所有的等式相加亦成立，所以aggregation verify成功。

4.2 proof of binding for same-commitment aggregation based on CDH-like assumption

若对于 $C,\{S^b,\vec{m}^b[S^b],\hat{\pi}^b\}_{b=0,1}$，存在 $i^*$，使得 $m_{i^*}^0\neq m_{i^*}^1$，则adversary作弊成功，相应的binding属性被破坏。

verify公式为： $e(C,g_2^{\sum_{i\in S}v_i})=e(\hat{\pi},g_2)\cdot g_T^{\sum_{i\in S}m_iu_iv_i}$
将 $\sum_{i\in S}v_i$表示为 $v_S$。
则上述作弊情况可表示为：
$e(C,g_2^{v_{S^0}})=e(\hat{\pi}^0,g_2)\cdot g_T^{\sum_{i\in S^0}m_i^0u_iv_i}$…<1>
$e(C,g_2^{v_{S^1}})=e(\hat{\pi}^1,g_2)\cdot g_T^{\sum_{i\in S^1}m_i^1u_iv_i}$…<2>
将等式<1>幂乘 $v_{S^1}$，将等式<2>幂乘 $v_{S^0}$，则有：
$e(\hat{\pi}^0,g_2^{v_{S^1}})\cdot g_T^{v_{S^1}\sum_{i\in S^0}m_i^0u_iv_i}= e(\hat{\pi}^1,g_2^{v_{S^0}})\cdot g_T^{v_{S^0}\sum_{i\in S^1}m_i^1u_iv_i}$
将有冲突的位置 $i^*$拆出来，有：

由于 $m_{i^*}^1 - m_{i^*}^0\neq 0$，于是根据上图公式可计算 $g_t^{u_{i^*}v_{i^*}^2}$的值，从而违背了CDH-like static assumption。

5. Weak binding

weak binding是指adversary （输入任意消息）honestly执行了Commit运算来生成commitment $C$，而不是任意选择了 $C$值。
满足AGM模式的叫做algebraic adversary。

对于 $C,\vec{m},r,(\hat{\pi},S,\vec{m}^*[S])$：

• $C=Commit(\vec{m};r)$
• $Verify(C,S,\vec{m}^*[S],\hat{\pi})=1$
• $\vec{m}[S]\neq\vec{m}^*[S]$
  Weak binding是指以上三个条件都成立的概率可忽略。

Challenger与Adversary之间相互交互：【借助same-commitment aggregation中proof of binding思路】

6. Cross-Commitment Aggregation from Polynomial Commitments

在Boneh, Drake, Fisch, and Gabizon 2020年论文《Efficient polynomial commitment schemes for multiple points and polynomials》 （基于Kate等人2010年论文《Constant-size commitments to polynomials and their applications》和Maller等人2019年论文《Sonic: Zero-knowledge SNARKs from linear-size universal and updatable structured reference strings》）的第3节算法的基础上，本文利用polynomial commitment 实现了支持cross-commitment aggregation 的vector commitment。
本文也采用Fiat-Shamir transform，同时做了如下改进：

• a commitment to a polynomial $P$ of degree $N-1$ can be thought of as commitment to the vector $(P(1),\cdots,P(N))$。
• 将在Boneh, Drake, Fisch, and Gabizon 2020年论文《Efficient polynomial commitment schemes for multiple points and polynomials》论文中的batch open算法分解为了single openings+aggregation。
• 将cross-commitment的verification方程式中的powers of a single random value $\gamma$ 改为了independent random $t_j$。【其实两个都可以，只是为了保持一致性做了该修改调整。—— 依据Gabizon等人2019年论文《PLONK: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge》】

[Gab20] 中指出，polynomial commitment初始设计时并不支持efficient updates，在本文中，可通过a bit of precomputation 来支持efficient update。其它算法的执行效率基本相当（up to constant factors），除了VerifyAcross算法，需要额外增加 $\Theta(lN)$个exponentiations运算（depending on the exact subsets being aggregated）。

Boneh, Drake, Fisch, and Gabizon [BDFG20] 2020年论文《Efficient polynomial commitment schemes for multiple points and polynomials》第4节的算法执行效率更高，但是该算法似乎无法支持cross-commitment aggregation。【because the second element of the proof (denoted $W’$ in [BDFG20]) depends on a random value that itself depends on the first element of the aggregated proof (denote $\pi$ the description of AggregateAcross below and $W$ in [BDFG20]).】

6.1 基于polynomial commitment实现same-commitment aggregation

6.2 基于polynomial commitment实现cross-commitment aggregation

6.2.1 proof of correctness for the cross-commitment aggregation based on polynomial commitment

6.2.2 proof of binding for the cross-commitment aggregation based on polynomial commitment

Binding holds under a $q$-type assumption in the AGM+ROM model。具体参见Boneh, Drake, Fisch, and Gabizon 2020年论文《Efficient polynomial commitment schemes for multiple points and polynomials》第3节内容。