Proofs for Inner Pairing Products and Applications 学习笔记

1. 引言

Benedikt Bünz 等人（standford,ethereum,berkeley） 2019年论文《Proofs for Inner Pairing Products and Applications》、

视频介绍：（2020年3月31日）
https://www.youtube.com/watch?v=oYdkGIoHKt0

代码实现：
https://github.com/scipr-lab/ripp

---

通过巧妙构建commitment key $\vec{v},\vec{w}$，可在4.4节GIPA实现的基础上，借助polynomial commitment，进一步优化Verifier的算力。【具体参见5.2.1节】

---

1.1 Pairing-based cryptography

Pairing-based cryptography可用于构建：

• 有效的签名——如BLS签名。BLS signature 来自于Boneh,Lynn和Shacham 2001年论文《Short signatures from the Weil pairing》。（参见博客 ECDSA VS Schnorr signature VS BLS signature 第3节内容）

• zero-knowledge proofs——如 Groth等人[GS08] 2008年论文《Efficient Non-interactive Proof Systems for Bilinear Groups》 和 Gennaro等人 [GGPR13] 2013年论文《Quadratic Span Programs and Succinct NIZKs without PCPs》。

• anonymous credentials——如Belenkiy等人 [BCLK08] 2008年论文《P-signatures and noninteractive anonymous credentials》。

以上这些协议均中，Verifier均需要借助pairings 来check bilinear relation between committed secrets。
如secret 信息 $(a,b)$，分别commit to $(a,b,ab)$ 为 $(C=g^{ab},g^a,g^b)$，验证 $e(C,g)=(g^a,g^b)$即可。

使用bilinear pairing可用于check a quadratic equation （二次方程式）in unkown variables is satisfied，如：

• 在 [GOS06] 中用于构建NIZK arguments in plain model。
• 在[PGHR13]中用于构建SNARKs with constant sized verifier。
• 在[PS16]中用于构建rerandomizable signature schemes。

1.2 GIPA（generalized inner product argument）

本文提出了generalized inner product argument (GIPA) 用于 pairing based languages，以解决：

• 将pairing equation运算外包给更powerful的prover；
• 证明committed source group elements are in pairing based languages；
• 构建polynomial commitment scheme，具有constant-sized commitments和efficient openings。

本文的GIPA是a generalization of the inner product argument for discrete logarithm relations。（具体可参见Bootle等人2016年论文[BCCGP16] Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting 和 Bünz等人2018年论文 [BBBPWM18] Bulletproofs: Short Proofs for Confidential Transactions and More）

本文构建了2中GIPA：

• SIPP：即statistical inner pairing product proof。
• TIPP：即trusted setup inner pairing product agrument of knowledge used demonstrate that certain pairing relations hold between committed group elements。

1.2.1 SIPP（statistical inner pairing product proof）

SIPP协议可用于outsource $n$ arbitrary pairings to a prover。

• Prover：运行SIPP来create a log-sized, publicly verifiable proof of the correct computation of an inner pairing product with respect to public source group elements。

• Verifier：只需计算一次pairing和一次variable-base multi-exponentiation of size $n$ in each source group。（计算开销：group exponentiation < pairing，现有的multi-exponentiation算法仅需要 $\mathcal{O}(n/\log n)$次exponentiation运算。）

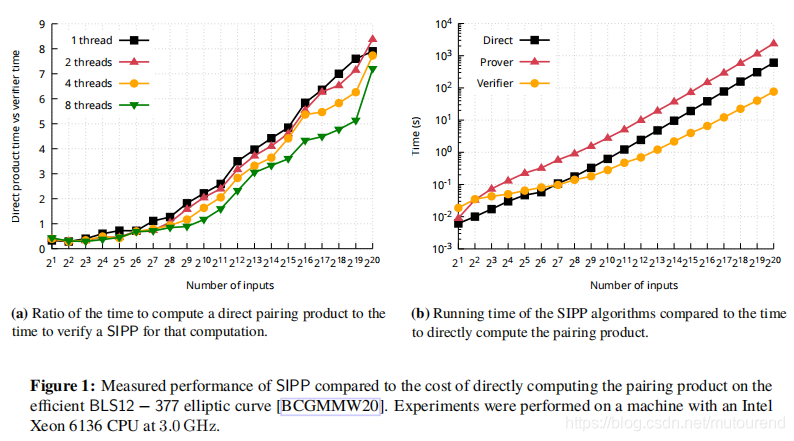
相比于Verifier 直接进行pairing product，SIPP可渐近地减少Verifier进行cryprographic operations的数量（随着pairing product的数量增加，优势越明显。），当pairing product的数量大于128时，SIPP verify就有优势；当pairing数量达到百万级时，SIPP verify的速度大于 $8\times$ faster，同时prove的速度也比直接计算快 $3-4\times$。

可用SIPP用于构建a new aggregate signature for BLS with a faster verifier than previous results ([BGLS03], [RY07], [BDN18] Boneh等人2018年论文《Compact Multi-signatures for Smaller Blockchains》。).【参见博客 Compact Multi-Signatures for Smaller Blockchains学习笔记】

1.2.2 TIPP（trusted setup inner pairing product）

TIPP具有logarithmic proof size and verifier time, and linear prover time (all with small contants)。相比于直接计算，TIPP的prover time可提升 $9-12\times$。

可将TIPP用于an untrusted party to aggregate $n$ Groth16 SNARKs （[Gro16] Groth 2016年论文《On the Size of Pairing-Based Non-interactive Arguments》） into a single log-sized proof with a log-time verifier。

An alternative to using SIPP or TIPP is to prove the same relations by using NP-reductions and a general purpose SNARK. 与[Gro16]的constant-size proof相比，本文的SIPP和TIPP protocols均为logarithmic proof size，但是SIPP和TIPP有 much faster prover time and greater compatibility with existing systems。

对于general purpose SNARKs，通常需要利用pairing-friendly cycles （如 [BCTB14] 2014年 Ben-Sasson等人论文《Scalable Zero Knowledge via Cycles of Elliptic Curves》）或者 two-chains（如论文[BCGMMW20] 2020年《Zexe: Enabling Decentralized Private Computation》）来将pairing based languages高效表示为arithmetic circuits。 而现有已知的cycles和two-chains，如果想达到128-bit security level的话，则需要大约780-bit curves/380-bit curves when recursion is not necessary。而要找到效率更高的pairing-friendly cycles并不容易，现有的curve family也有一些缺陷，具体参看论文[CCW19] On Cycles of Pairing-Friendly Elliptic Curves。

即使使用pairing-friendly cycles将statements reduce to arithmetic circuits (or R1CS)，the NP-language for general purpose SNARKs，is very expensive。如 a signle pairing operation requires about 15,000 R1CS constraints to express。而[Gro16] SNARK 算法的proving time与constraints的数量呈quasi-linear关系。

1.3 Polynomial commitment (PC)

Polynomial commitment由[KZG10] Kate等人 2010年论文《Constant-Size Commitments to Polynomials and Their Applications》 首次提出，具体是指：

• committer输出一个short commitment to polynomial；
• committer输出一个short proof （或者opening），用于证明the correctness of an evaluation of that committed polynomial at any point。

Polynomial commitment (PC) 在很多领域用于reduce communication and computation costs，如：

• proofs of storage and replication [XYZW16] [Fis18]；
• anonymous credentials [CDHK15] [FHS19]；
• verifiable secret sharing [KZG10] [BDK13]；
• zero-knowledge arguments [WTSTW18] [MBKM19] [Gab19] [Set19] [GWC19] [XZZPS19] [CHMMVW20]。

本文将polynomial commitment与inner product argument结合，构建了a pairing based inner product argument，具有constant-sized commitments、logarithmic-sized openings 和 square root reference string。

本文采用了与[Gro11] 中类似的two-tiered homomorphic commitment，同时支持单变量和双变量多项式。本文提供了一种实例化方式，使得其同时具有public-coin setup, achieving square root verifier time以及upadatable SRS [GKMMM18]，achieving log-time verification。

The transparent variant is secure in the plain model under the standard SXDH assumption，而本文的trusted setup scheme is secure in the algebraic group model (AGM) [FKL18]。本文的这种trusted setup scheme 具有的优势主要体现在produce opening proofs的时效上：

• 对于单变量多项式，opening cost为square root in the degree of the polynomial；
• 对于双变量多项式，opening cost为linear in the degree of one variable。

1.3.1 现有各种polynomial commitment对比

• [KZG10] 的trusted setup scheme 支持constant proof size and verifier time （而本文的算法是logarithmic），但是本文的算法quadratically improve the opening efficiency，同时the maximum degree polynomial supported by a SRS of a given size。更小的SRS有助于节约storage，提升setup效率，而且还有助于security。
  Gurk等人在论文[GGW18] 中指出，Cheon‘s attck on q-type assumption [Che10] can degrade the security of some SNARK schemes over BLS12-381 from the advertised 128 bits of security to 114 bits of security。
  [KZG10] 论文中的scheme is secure under an updatable setup in the algebraic group model。

• [Gro11] 论文中 designed a pairing based “batch product argument” secure under SXDH。该argument可看作是一种类型的polynomial commitment scheme。

• [BG13] 论文中 Bayer和Groth designed a zero-knowledge proving system to show that a committed value is the correct evaluation of a known polynomial, under discrete-logarithm assumption。

• [WTSTW18] 论文中 Wahby等人证明了可借用Bulletproofs中的inner product argument 来构建polynomial commitment scheme。

• [BGH19] 论文中 Bowe等人证明了Bulletproofs的inner product argument 是可highly aggregatable to the point where aggregated proofs can be verified using a one off linear cost and an additional logarithmic factor per proof。

• [ZXZS19] 论文中使用Reed-Solomon codes构建了polynomial commitment scheme。该论文中的commtiment使用了highly efficient symmetric key primitives，however the protocols that use them require soundness boosting techniques that result in large constant overheads。

• [BFS19] 论文中 Bünz等人借助groups of unkown order such as RSA groups or class groups构建了polynomial commitment scheme，具有efficient verifier time and small proof size，但是需要super-linear commitment and prover time。

1.4 密码学假设

1.4.1 $q$-DBP q-Double pairing assumption

根据[AFGHO16]，该假设在SXDH assumption下是安全的。

1.4.2 $q$-ASDBP q-Auxiliary Structured Double Pairing assumption

1.4.3 $q$-SDH q-Strong Diffie-Hellman assumption

1.5 一些应用

• 用于Aggregating pairing-based SNARKs：基于本文的TIPP算法，构建an aggregator for Groth16 [Gro16] pairing-based SNARKs。 aggregated proof具有logarithmic size，verifier computation 则depend on the cost of uploading the instances in addition to a logarithmic number of target group exponentiations。 本文构建了一层recursive proofs (如，a proof of proofs)，既不依赖于抵消的pairing-friendly cycles or two-chains，也不依赖于昂贵的NP reductions。

• 用于Aggregating BLS signatures：基于本文的SIPP算法，用于aggregate BLS signatures。[BGLS03] 论文中的BLS signature aggregate算法需要Verifier to compute one pairing per distinct message。而使用SIPP算法，其verification 只需要compute a single pairing and a multi-exponentiation in each source group of size equal to the number of messages being verified。但是本文的aggregated siganture是logarithmic的，而[BGLS03]中的aggregated signature是constant-size的。但是本文的aggregation算法可computed offline by any untrusted party who requires no secrets。

1.6 inner pairing product protocol相关工作

• 在Lai等人2019年论文[LMR19] 《Succinct Arguments for Bilinear Group Arithmetic: Practical Structure-Preserving Cryptography 》中的inner product argument for pairing based languages，具有如下特性：
  – 具有transparent setup；
  – secure under the SXDH assumption；
  – 可用于zero-knowledge proofs。

• Groth等人2008年论文[GS08] 中提供了一种算法用于 prove pairing-based languages under zero-knowledge without reducing to NP (or alternatively under witness indistinguishably with smaller proofs)。

现有的inner pairing product protocol性能对比：

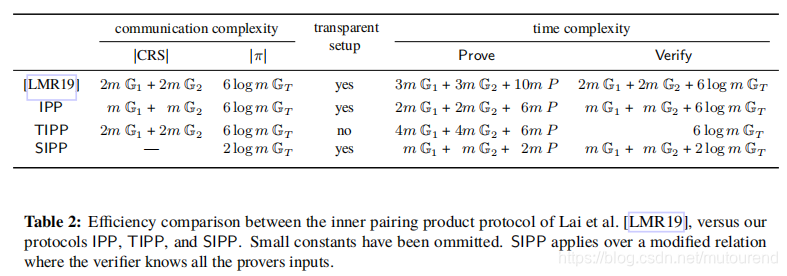
Abe等人在2016年论文[AFGHO16] 《Structure-Preserving Signatures and Commitments to Group Elements》中证明了：在double pairing assumption下，one can commit to group elements in asymmetric bilinear groups。该技术可用于构建structure preserving signatures (如，messages为group elements的signatures) in the standard model。本文借助了这种commitment scheme。

2. 技术要点

2.1 GIPA (Generalized Inner Product Argument)

本文的核心就是generalized inner product argument，在Bootle等人2016年论文[BCCGP16] Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting 和 Bünz等人2018年论文 [BBBPWM18] Bulletproofs: Short Proofs for Confidential Transactions and More的基础上，使用了具有doubly homomorphic属性的commitment scheme，满足：
$CM((ck_1+ck_2),(M_1+M_2))=CM(ck_1,M_1)+CM(ck_1,M_2)+CM(ck_2,M_1)+CM(ck_2,M_2)$

inner product具有bilinear属性，满足：
$<\vec{a}+\vec{b},\vec{c}+\vec{d}>=<\vec{a},\vec{c}>+<\vec{a},\vec{d}>+<\vec{b},\vec{c}>+<\vec{b},\vec{d}>$

对比以上两个公式可发现，二者结合可用于generalized inner product argument。

GIPA (Generalized Inner Product Argument) 可分为如下三种类型的inner product：

• $<,>:\mathbb{G}_1^m\times \mathbb{G}_2^m\rightarrow \mathbb{G}_T,<\vec{A},\vec{B}>=\prod_{i=0}^{m-1}e(A_i,B_i)$
• $<,>:\mathbb{G}_1^m\times \mathbb{F}^m\rightarrow \mathbb{G}_1,<\vec{A},\vec{b}>=\prod_{i=0}^{m-1}A_i^{b_i}$
• $<,>:\mathbb{F}^m\times \mathbb{F}^m\rightarrow \mathbb{F},<\vec{a},\vec{b}>=\prod_{i=0}^{m-1}a_ib_i$

本文：

• 采用第一种inner product来obtain SIPP with respect to the identity commitment。
• 采用第一种inner product来obtain TIPP with respect to a commitment scheme that has a structured commitment key。

本文实际采用的commit算法是与Abe等人在2016年论文[AFGHO16] 《Structure-Preserving Signatures and Commitments to Group Elements》中的一样：

• commitment key $(v_0,v_1)\in\mathbb{G}_2^2$。
• 待commit的信息为 $(A_0,A_1)\in\mathbb{G}_1^2$。
• 对应的commitment为 $e(A_0,v_0)e(A_1,v_1)$。

通过使用structured setup，在GIPA中Verifier计算的components也是highly structured的，具体的为 a KZG [KZG10] polynomial commitment为：

• polynomial信息为 Bowe等人 [BGH19] 论文中（提到的可computed in logarithmic time）的polynomial。

因此可将verifier的work outsource to the pover。相应的Prover只需要证明：
their honest intent by opening the KZG commitment to the correct evaluation (which the verifier computes themselves)。

2.2 Polynomial commitment

本文采用的是Groth [Gro11] 中的 two-tiered homomorphic commitments，即：commitments to commitments。

假设要commit to a polynomial：
$f(X,Y)=f_0(Y)+f_1(Y)X+\cdots+f_{m-1}(Y)X^{m-1}=\sum_{i=0}^{m-1}f_i(Y)X^i$

可将polynomial $f(X,Y)$ 以矩阵形式表示为：
$f(X,Y)=(1,X,X^2,\cdots,X^{m-1})\begin{pmatrix} a_{0,0} & a_{0,1} & a_{0,2} & \cdots & a_{0,l-1}\\ a_{1,0} & a_{1,1} & a_{1,2} & \cdots & a_{1,l-1}\\ a_{2,0} & a_{2,1} & a_{2,2} & \cdots & a_{2,l-1}\\ \vdots & & & \ddots & \vdots\\ a_{m-1,0} & a_{m-1,1} & a_{m-1,2} & \cdots & a_{m-1,l-1} \end{pmatrix} \begin{pmatrix} 1\\ Y\\ Y^2\\ \cdots \\ Y^{l-1} \end{pmatrix}$

则commit to $f(X,Y)$ 可表示为：

• 先对polynomials $f_0(Y),\cdots,f_{m-1}(Y)$进行commit，相应的commitment值依次为 $A_0,\cdots,A_{m-1}$。
• 再对 $A_0,\cdots,A_{m-1}$进行commit，其commitment值为 $T=CM(A_0,\cdots,A_{m-1})$。

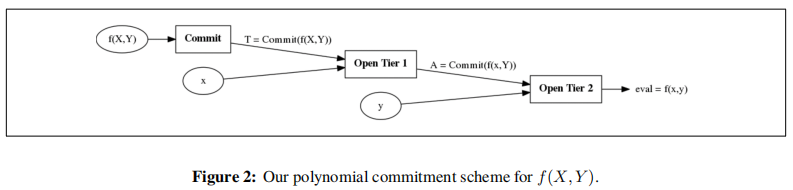
如上图所示，当收到challenge $(x,y)$ 时，Prover：

• 先在第一层 evalute at $x$ to obtain a commitment $A$ to $f(x,Y)$。可通过multiexponentiation IPP argument (MIPP) 来实现。
• 然后在第二层 open commitment $A$ at $y$ 来获取 $eval=f(x,y)$。这可利用单变量polynomial commitment scheme来实现。
  – 若在第二层采用Bulletproofs （Bünz等人2018年论文 [BBBPWM18] Bulletproofs: Short Proofs for Confidential Transactions and More）方式来实现，则对应的是transparent version。
  – 若在第二层采用的是KZG方式，则对应的是structured setup version。

2.3 一些定义

3. 通过SIPP Outsourcing inner pairing products

使用 an interactive, RBR sound inner pairing product (SIPP) 来生产proofs of pairing products。

RBR（Round-by-round）soundness是指：

SIPP requires no setup and is public-coin。

使用SIPP：

• Verifier不再需要直接进行 $n$ 次pairing计算，而改为只需要计算 $n$次exponentiations或者two multi-exponentiations of size $n$ in the source groups。
• Prover 需要进行 $2n$次pairing计算，并发送 $2\log(n)$个target group proof elements给Verifier。

3.1 SIPP的构建

SIPP对应的language表示为：
$\mathcal{L}_{SIPP}=\{(\vec{A}\in\mathbb{G}_1^m,\vec{B}\in\mathbb{G}_2^m,Z\in\mathbb{G}_T):Z=\vec{A}*\vec{B}\}$

假设 $m$为二次幂，则可通过递归法，将vectors $\vec{A},\vec{B}$切分为长度为 $m'=m/2$的new vectors $\vec{A}',\vec{B}'$，使得 $\vec{A}'*\vec{B}'=Z'$。使用Verifier生成的challenge，Prover和Verifier可以独立允许该递归算法。

首先，Prover commit to a pair of target group elements $(Z_L, Z_R)$。Verifier可利用 $(Z_L, Z_R)$来生成 $m'=1$的情况（即对应为last round）的 a new target group element $Z'$，Verifier只需验证 $e(A',B')=Z'$ 成立即可（in the final round of recursion where $m'=1$）。

基本信息为：

• public info： $\vec{A}\in\mathbb{G}_1^m,\vec{B}\in\mathbb{G}_2^m$以及 $Z\in\mathbb{G}_T$
• 待证明： $Z=\vec{A}*\vec{B}=\prod_{i=0}^{m-1}e(A_i,B_i)$

需要执行 $\log(m)$ 轮 recursive protocol。
详细的interactive证明过程为：（ $m'=m/2$开始， $m'=1$结束。）

• （1）Prover：输入为 $(\vec{A},\vec{B},Z,m)$，设置 $m'=m/2$，计算 $Z_L=\vec{A}_{[m':]}*\vec{B}_{[:m']},Z_R=\vec{A}_{[:m']}*\vec{B}_{[m':]}$，将 $(Z_L,Z_R)$发送给Veriifier。
• （2）Verfier：取随机数 $x\overset{r}{\leftarrow} \mathbb{F}$，将challenge $x$发送给Prover。
• （3）Prover和Verifier同时计算： $\vec{A}'=\vec{A}_{[m':]}^x\circ\vec{A}_{[:m']},\vec{B}'=\vec{B}_{[m':]}^{-x}\circ\vec{B}_{[:m']}$
• （4）Verifier计算： $Z'=Z_L^x\cdot Z\cdot Z_R^{-x}$。Verifier验证 $e(\vec{A}',\vec{B}')=Z'$是否成立，若成立则继续，否则返回0。【此处可不验证，只在最后 $m'=1$时才做验证】
• （5）若 $m'>1$，则设置 $(\vec{A},\vec{B},Z,m)=(\vec{A}',\vec{B}',Z',m')$，继续步骤（1）。
• （6）若 $m'=1$，则Verifier验证 $e(A',B')=Z'$是否成立，若成立则返回1，否则返回0。【Verifier仅需进行1次pairing计算】

以上interactive证明成立，遵循的是 DeMillo-Lipton-Schwartz-Zippel lemma，即：
the prover must commit to the coeeficients of a polynomial that is then evaluated at a random point。
对于任意的随机数 $x\overset{r}{\leftarrow} \mathbb{F}$，伪造 $Z_L,Z,Z_R$使得如下等式成立的概率可忽略：
$Z'=\vec{A}'*\vec{B}'\Leftrightarrow Z_L^x\cdot Z\cdot Z_R^{-x}=(\vec{A}_{[m':]}*\vec{B}_{[:m']})^x\cdot \vec{A}*\vec{B}\cdot (\vec{A}_{[:m']}*\vec{B}_{[m':]})^{-x}$。
因此，Verifier无需在每个round都做check，仅需在 $m'=1$时，验证 $e(A',B')=Z'$是否成立即可。

3.2 SIPP的计算复杂度

整个SIPP协议，存在 $\log(m)$ rounds，每个round Prover都发送2个target group elements $(Z_L,Z_R)$给Verifier，也就是说总的proof size为 $2\log(n)$个target group elements。
Prover和Verifier的计算复杂度比较：

• Prover为了计算 $(Z_L,Z_R)$，在第一轮需要进行 $m$次pairing计算，在第二轮需要 $m/2$次pairing计算，而在第 $i$轮，需要的pairing计算此参数为 $m/2^i$次。 $\log(m)$轮，Prover需要计算pairing的总次数为 $\sum_{i=0}^{\log(m)-1}m/2^i=2m$次。【？】
• Verifier仅需在最后一轮进行1次pairing计算。
• 在每一轮，Prover和Verifier均需要计算 $\vec{A}'=\vec{A}_{[m':]}^x\circ\vec{A}_{[:m']},\vec{B}'=\vec{B}_{[m':]}^{-x}\circ\vec{B}_{[:m']}$。 $\log(m)$轮，Prover和Verifier分别均需分别在 $\mathbb{G}_1和\mathbb{G}_2$ groups 下总共计算 $m$次exponentiations。
• 在每一轮，Verifier均需计算 $Z'=Z_L^x\cdot Z\cdot Z_R^{-x}$。 $\log(m)$轮，Verifier总共需计算 $2\log(n)$次exponentiations in $\mathbb{G}_T$。

3.3 SIPP的security

SIPP具有perfect completeness和RBR soundness，详情参见论文4.3节内容。

3.4 SIPP 用于reduce pairings to a pairing product

很多证明系统最终验证的形式为 $e(A_i,B_i)=e(C_i,D_i)$，借助random linear combination，SIPP可用与outsource $m$ 个类似这样的pairing checks。
核心思想为：若 $e(A_i,B_i)=e(C_i,D_i)$ 成立，则对于任意的 $r\leftarrow \mathbb{F}_p$， $e(A_i,B_i)^{r^i}=e(C_i,D_i)^{r^i}$均成立，也即 $e(A_i^{r^i},B_i)e(C_i^{-r^i},D_i)=1$成立。
对 $m$个这样的等式进行线性组合，有：
$\prod_{i=1}^{m}e(A_i^{r^i},B_i)e(C_i^{-r^i},D_i)=1$应成立。

由此，将 $m$个任意的pairing check reduce to an inner pairing product of length $2m$。

若Verifier直接验证的话，需要计算 $2n$次pairing。
若借助SIPP协议，则相当于设置 $\vec{A}=(A_1^r,A_2^{r^2},\cdots,A_m^{r^m},C_1^{-r},C_2^{-r^2},\cdots,C_m^{-r^m})=(\mathcal{A}_1,\mathcal{A}_2,\cdots,\mathcal{A}_m,\mathcal{A}_{m+1},\mathcal{A}_{m+2},\cdots,\mathcal{A}_{2m}),\vec{B}=(B_1,B_2,\cdots,B_m,D_1,D_2,\cdots,D_m)=(\mathcal{B}_1,\mathcal{B}_2,\cdots,\mathcal{B}_m,\mathcal{B}_{m+1},\mathcal{B}_{m+2},\cdots,\mathcal{B}_{2m})$，证明 $\vec{A}*\vec{B}=1$。

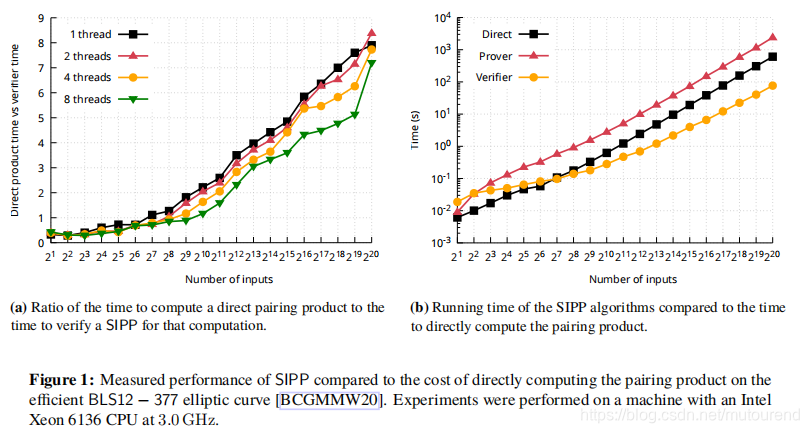
3.5 SIPP的性能表现

实际基于Zexe的BLS12-377 elliptic curve做了代码实现，并对比了直接计算pairing products和通过Pippenger’s fast multi-exponentiation 算法的效率。当pairing products的数量大于128个时，基于SIPP的verifier性能有优势，而当有 $2^20$次个pairing products时，性能将优于 $8\times$。

4. GIPA (Generalized Inner Product Argument)

接下来，需要对[BCCGP16][BBBPWM18]的 inner product argument 的基础上，构建doubly-homomorphic inner product commitments，满足：
$CM((ck_1+ck_2)，(M_1+M_2))=CM(ck_1,M_1)+CM(ck_1,M_2)+CM(ck_2,M_1)+CM(ck_2,M_2)$

4.1 doubly homomorphic commitment定义

Pedersen commitment可看成是doubly homomorphic commitment，因为：

4.2 inner product定义

可将inner product可看成是一个map，用于map two vectors to a group in a manner that satisfies bilinearity。inner product 定义为：

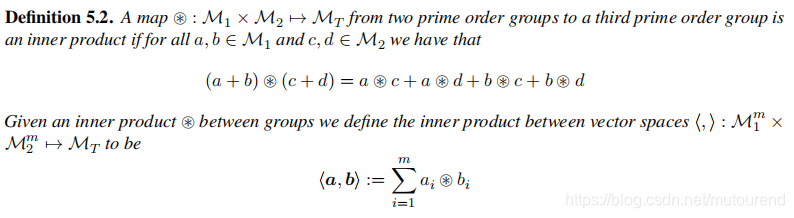
如2.1节所述，本文主要关注三种类型的inner product：

• $<,>:\mathbb{G}_1^m\times \mathbb{G}_2^m\rightarrow \mathbb{G}_T,<\vec{A},\vec{B}>=\prod_{i=0}^{m-1}e(A_i,B_i)$【SIPP等pairing based 协议】
• $<,>:\mathbb{G}_1^m\times \mathbb{F}^m\rightarrow \mathbb{G}_1,<\vec{A},\vec{b}>=\prod_{i=0}^{m-1}A_i^{b_i}$【论文第5章主要关注这个】
• $<,>:\mathbb{F}^m\times \mathbb{F}^m\rightarrow \mathbb{F},<\vec{a},\vec{b}>=\prod_{i=0}^{m-1}a_ib_i$ 【bulletproofs [BBBPWM18]中的commitment scheme 实例化为 $CM((\vec{g},\vec{h});(\vec{a},\vec{b}))=\vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{<\vec{a},\vec{b}>}$。】

4.3 inner product commitment定义

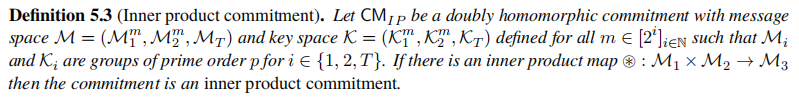
则设置 $CM((\vec{ck}_1,\vec{ck}_2,ck_3);(M_1,M_2,<M_1,M_2>))$为 a binding inner product commitment。
以下均假设message space dimension为二次幂，即vector长度为二次幂。

4.4 GIPA的构建

基本信息为：

• public info： $ck=(\vec{ck}_1,\vec{ck}_2,ck_3)$以及inner product commitment $C$。
• private info： $\vec{a},\vec{b}$
• 待证明： $C=CM((\vec{ck}_1,\vec{ck}_2,ck_3);(\vec{a},\vec{b},<\vec{a},\vec{b}>))$

其实即为an argument of knowledge given a binding inner product commitment。

需要执行 $\log(m)$ 轮 recursive protocol。
详细的interactive证明过程为：（ $m'=m/2$开始， $m'=1$结束。）

• （1）Prover：public 输入为 $(ck,C,m)$，private 输入为 $(\vec{a},\vec{b})$，设置 $m'=m/2$，计算 $z_L=<\vec{a}_{[m':]},\vec{b}_{[:m']}>,z_R=<\vec{a}_{[:m']},\vec{b}_{[m':]}>,C_L=CM(ck;(\vec{a}_{[m':]},\vec{b}_{[:m']},z_L)),C_R=CM(ck;(\vec{a}_{[:m']},\vec{b}_{[m':]},z_R))$，将 $(C_L,C_R)$发送给Veriifier。
• （2）Verfier：取随机数 $x\overset{r}{\leftarrow} \mathbb{F}$，将challenge $x$发送给Prover。
• （3）Prover计算： $\vec{a}'=x\cdot \vec{a}_{[m':]}+\vec{a}_{[:m']},\vec{b}'=x^{-1}\cdot \vec{b}_{[m':]}+\vec{b}_{[:m']}$
• （4）Prover和Verifier同时计算： $\vec{ck}_1'=x^{-1}\cdot\vec{ck}_{1,[:m']}+\vec{ck}_{1,[m':]},\vec{ck}_2'=x\cdot\vec{ck}_{2,[:m']}+\vec{ck}_{2,[m':]}$
• （5）Verifier计算： $C'=x\cdot C_L + C + x^{-1}\cdot C_R$。
• （5）若 $m'>1$，则设置 $ck=(\vec{ck}_1',\vec{ck}_2',ck_3),\vec{a}=\vec{a}',\vec{b}=\vec{b}',m=m/2$，继续步骤（1）。
• （6）若 $m'=1$，可设置 $a=\vec{a}',b=\vec{b}',ck=(\vec{ck}_1',\vec{ck}_2',ck_3),C=C'$，则Verifier验证 $CM(ck;(a,b,<a,b>)=C)$是否成立，若成立则返回1，否则返回0。

4.5 GIPA的security

GIPA具有perfect completeness和computational witness-extended emulation，详情参见论文5章内容。

4.6 GIPA的计算复杂度

整个GIPA有 $\log_{2}(m)$ 个rounds，有 $2\log_{2}(m)$个commitments。在有一些应用场景，part of the commitment can be computed from the verifier’s input and don’t need to be transmitted。【？】

Prover依次produce commitments for vectors of length $m/2,m/4,m/8,\cdots$。相应的，The total length of all committed vectors为 $4\cdot \log_2m$。【？】

Verifier在每个round都会计算 $C'=x\cdot C_L + C + x^{-1}\cdot C_R$。总共会计算 $2\log_{2}(m)$次scalar multiplications in $Image(CM)$。

Prover和Verifier在每个round都会计算 $\vec{ck}_1'=x^{-1}\cdot\vec{ck}_{1,[:m']}+\vec{ck}_{1,[m':]},\vec{ck}_2'=x\cdot\vec{ck}_{2,[:m']}+\vec{ck}_{2,[m':]}$。总共会计算 $2\cdot \log_{2}m$次scalar multiplications in $\mathcal{K}$。

借助Bünz等人2018年论文 [BBBPWM18] Bulletproofs: Short Proofs for Confidential Transactions and More 中的技术，the verifier can use a single large multi-exponentiation in $\mathcal{K}$ to compute the final $ck$。

Verifier仅需做一次 $<a,b>$inner product 计算。这对于在pairing settings场景下，inner product 计算 significantly more expensive than scalar multiplications in $\mathcal{K}$。

可使用 Fiat-Shamir heuristic for logarithmic round public coin protocols【In the random oracle model the heuristic is secure for constant-round protocols and for multi-round protocols satisfying soundness against restoration attacks functions [FS86; BCS16; CCHLRR18]】，将GIPA转为non-interactive and publicly verifiable协议。chanllenge $x$不再来自于Verifier，而来自于 a hash function $Hash$ applied to the transcript。Verifier也可以check that all challenges were computed correctly。

4.7 GIPA实例化

GIPA可通过不同的commitments来实例化：

• 如Bünz等人2018年论文 [BBBPWM18] Bulletproofs: Short Proofs for Confidential Transactions and More 中采用Pedersen commitment来实例化：
  $CM((\vec{g},\vec{h});(\vec{a},\vec{b}))=\vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{<\vec{a},\vec{b}>}$
  其中 $\vec{g}\in\mathbb{G}^m,\vec{h}\in\mathbb{G}^m,u\in\mathbb{G},\vec{a},\vec{b}\in\mathbb{F}_p^m$ for a group $\mathbb{G}$ of prime order $p$。
  若the discrete logarithm assumption holds for $\mathbb{G}$，则该commitment具有binding属性，

• Lai等人2019年论文[LMR19] 《Succinct Arguments for Bilinear Group Arithmetic: Practical Structure-Preserving Cryptography 》中采用pairing commitment来实例化：
  $CM((\vec{v}_1,\vec{v}_2,\vec{w}_1,\vec{w}_2);(\vec{A},\vec{B}))=((\vec{A}*\vec{v}_1)\cdot(\vec{w}_1*\vec{B}),(\vec{A}*\vec{v}_2)\cdot(\vec{w}_2*\vec{B}),\vec{A}*\vec{B})$
  [LMR19] 论文中指出，该commitment部分内容Verifier可直接根据其输入计算，这样Prover就不再需要传输该部分commitment内容，提高效率。

在[LMR19] 的基础上，借助SIPP commitment，可将SIPP转化为GIPA的一种实例化方式。

4.7.1 SIPP commitment定义

• inner pairing product： $*:\mathbb{G}_1^m\times\mathbb{G}_2\rightarrow \mathbb{G}_T,\vec{A}*\vec{B}=\prod_{i=1}^{m}e(A_i,B_i)$
• $SIPP.CM((\vec{a},\vec{b},z),(\vec{A},\vec{B},Z))=((A_0^{a_0},\cdots,A_{m-1}^{a_{m-1}}),(B_0^{b_0},\cdots,B_{m-1}^{b_{m-1}}),Z^z)$
  其中 key space为 $(\vec{a},\vec{b},z)\in \mathbb{F}^m\times\mathbb{F}^m\times\mathbb{F}$，message space为 $(\vec{A},\vec{B},Z)\in \mathbb{G}_1^m\times\mathbb{G}_2\times\mathbb{G}_T$

4.7.2 GIPA用于改进[LMR19]的协议

Lai等人2019年论文[LMR19] 《Succinct Arguments for Bilinear Group Arithmetic: Practical Structure-Preserving Cryptography 》中的pairing commitment为：
$CM((\vec{v}_1,\vec{v}_2,\vec{w}_1,\vec{w}_2);(\vec{A},\vec{B}))=((\vec{A}*\vec{v}_1)\cdot(\vec{w}_1*\vec{B}),(\vec{A}*\vec{v}_2)\cdot(\vec{w}_2*\vec{B}),\vec{A}*\vec{B})$
当需要commit to 2 vectors of length $m$时，需要的commitment key length为 $4\cdot m$。

而Abe等人在2016年论文[AFGHO16] 《Structure-Preserving Signatures and Commitments to Group Elements》中的 SXDH assumption pairing commitment为：
$CM((\vec{v},\vec{w});(\vec{A},\vec{B},Z))=(\vec{A}*\vec{v},\vec{w}*\vec{B},Z)$
其中 key space为 $(\vec{v},\vec{w})\in \mathbb{G}_2^m\times\mathbb{G}_1^m$，message space为 $(\vec{A},\vec{B},Z)\in\mathbb{G}_1^m\times\mathbb{G}_2^m\times\mathbb{G}_T$，commitment space为 $(\vec{A}*\vec{v},\vec{w}*\vec{B},Z)\in\mathbb{G}_T^3$。
可以看出，在message space, key space和commitment space均为doubly homomorphic，所以该commitment也为an inner product commitment。
当需要commit to 2 vectors of length $m$时，需要的commitment key length为 $2\cdot m$。

[LMR19] 和 [AFGHO16] 的proof size 相同，但是 [AFGHO16]的commitment key size更小，可以节约Prover和Verifier的时间。
在该论文中，可通过structured setup 进一步节约verifier的时间，使其仅为logarithmic in the length of the committed vectors。

5. verifiable TIPP argument with SRS

基本信息为：

• public info： $C\in\mathbb{G}_T$
• private info： $\vec{A}\in\mathbb{G}_1^m,\vec{B}\in\mathbb{G}_2^m$
• 待证明： $C=\vec{A}*\vec{B}=\prod_{i=0}^{m-1}e(A_i,B_i)$

构建an inner pairing product argument，要求相比于直接传输 $\vec{A},\vec{B}$，具有significantly less communication。
基本思路为：

• prover and verifier reduce the $m$ equations to one using a random linear combination。
• prover commits to all $A_i,B_i$。
• verifier生成challenge $r\leftarrow \mathbb{F}$。
• prover convinces the verifier that $\prod_{i=1}^{m}e(A_i^{r^{2i}},B_i)=Z$。

基于以上思路构建的为GIPA的一种实例化，称为trusted inner pairing product $TIPP$。

借助[GKMMM18] （Groth等人2018年论文《Updatable and Universal Common Reference Strings with Applications to zk-SNARKs》）和[BGH19] （Bowe等人2019年论文《Halo: Recursive Proof Composition without a Trusted Setup》）的思路，本文在构建TIPP时使用 an updatable references string，使得Verifier can efficiently check that $ck_{final}$ was computed correctly。

5.1 doubly homomorphic commitment with structured key

在Abe等人2016年论文[AFGHO16] 《Structure-Preserving Signatures and Commitments to Group Elements》的pairing based commitment scheme的基础上，进行扩展。

在选择structure of SRS elements时，需要注意保证commitment scheme的binding 属性。

• commitment key为： $ck=(pair,\vec{w}=[g^{\alpha^{2i}}]_{i=0}^{m-1},\vec{v}=[h^{\beta^{2i}}]_{i=0}^{m-1})$

• commitment 算法为： $CM:\mathbb{G}_1^m\times\mathbb{G}_2^m\rightarrow \mathbb{G}_T^2$
  $CM((\vec{v},\vec{w});(\vec{A}.\vec{B}))=(\vec{A}*\vec{v},\vec{w}*\vec{B})=(T,U)$，其中key space为 $(\vec{v},\vec{w})\in\mathbb{G}_2^m\times\mathbb{G}_1^m$，message space为 $(\vec{A}.\vec{B})\in\mathbb{G}_1^m\times\mathbb{G}_2^m$，commitment space为 $(T,U)\in\mathbb{G}_T^2$。

• 除commitment key 外，Prover还具有的额外SRS信息为： $g^{\beta},h^{\alpha},\{g^{\alpha^i},h^{\beta^i}\}_{i=0}^{2m-2}$

注意，odd powers of $\alpha$ in $\mathbb{G}_1$，如 $g^{\alpha^{2i+1}}$并不使用，原因是：
避免使用SRS中的 $h^{\alpha}$来碰撞commitment，因为 $e(g,h^{\alpha})\cdot e(g^{\alpha},h^{-1})=1_{\mathbb{T}}$。

以上commitment在 $q$-ASDBP assumption下，具有binding属性。

5.2 TIPP的构建

基于5.1节的commitment scheme，基本信息变为：

• public info： $T,U,Z\in\mathbb{G}_T, \vec{w}\in\mathbb{G}_1^m, \vec{v}\in\mathbb{G}_2^m,r\in\mathbb{F}$
• private info： $\vec{A}\in\mathbb{G}_1^m,\vec{B}\in\mathbb{G}_2^m$
• 待证明： $T=\vec{A}*\vec{v}\wedge U=\vec{w}*\vec{B} \wedge \{A_i'=A_i^{r^{2i}}\}_{i=0}^{m-1} \wedge Z=\vec{A}'*\vec{B}=\prod_{i=0}^{m-1}e(A_i',B_i)=\prod_{i=0}^{m-1}e(A_i^{r^{2i}},B_i)$

其中：

• $Z=\vec{A}^{\vec{r}}*\vec{B}$。引入 $\vec{r}$ 有助于构建aggregator，如当需要将many pairings must be collapsed into one时， $\vec{r}$ is set to the vector of exponenets chosen by the verifier to do so。
• $T=\vec{A}*\vec{v}$可看成是a commitment to $\vec{A}$，同时 $T=\vec{A}^{\vec{r}}*\vec{v}^{-\vec{r}}$也可看成是a commitment to $\vec{A}^{\vec{r}}$ under the commitment key $\vec{v}^{-\vec{r}}$。

因此，在构建aggregator时，基本流程为：

• Prover：生成 $T,U$，并将 $(T,U)$发送给Verifier。
• Verifier：选择challenge $\vec{r}=\{1,r^2,r^4,\cdots,r^{2m-2}\}$.
• $\vec{A}$的commitment key变为 $\vec{v}'=\vec{v}^{-\vec{r}}$，基于 $(\vec{v}',\vec{w})$ 来执行剩余的protocol。

详细的实现细节为：

• Setup：分为了proving key 和 verifiying key
  
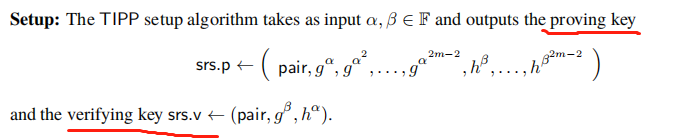
• Initialise初始化：public info为 $T,U,Z$和 $\vec{r}=\{1,r^2,r^4,\cdots,r^{2m-2}\}$和新的commitment key $\vec{v}'=\vec{v}^{-\vec{r}}$。最终转换为：The prover now aims to convince the verifier that they know an opening $\vec{A}',\vec{B}$ to $T,U$ under the commitment key $(\vec{v}',\vec{w})$ such that $Z=\vec{A}'*\vec{B}$。
• 证明：即可利用4.4节的"GIPA的构建"方法来证明，基于的doubly homomorphic commiment scheme为：
  $CM((\vec{v}',\vec{w},1);(\vec{A}',\vec{B},Z))=(\vec{A}'*\vec{v}',\vec{w}*\vec{B},Z)=(T,U,Z)$
  

注意上图，若采用4.4节中的算法，commitment key的递归计算方式为：
$\vec{v}'=\vec{v}_{[m':]}^{x^{-1}}\circ\vec{v}_{[:m']},\vec{w}'=\vec{w}_{[m':]}^{x}\circ\vec{w}_{[:m']}$
4.4节的算法中，Prover和Verifier均需要进行如上递归计算。而其实Verifier只需要 $m=1$时最后一个final round的 $v\in\mathbb{G}_1,w\in\mathbb{G}_2$值。
若Verifier想节约算力，改为由Prover直接提供 $v\in\mathbb{G}_1,w\in\mathbb{G}_2$值和相应的proof，Verifier值需要验证proof正确即可。

5.2.1 借助polynomial commitment优化verifier算力

注意：初始的 $\vec{w}=[g^{\alpha^{2i}}]_{i=0}^{m-1},\vec{v}=[h^{(\beta r^{-1})^{2i}}]_{i=0}^{m-1}$

对于 $n=\log(m)$轮， $l=n-1=\log(m)-1$，相应的challenges为 $\vec{x}=(x_0,\cdots,x_l)$,最终的 $v\in\mathbb{G}_1,w\in\mathbb{G}_2$具有如下relation：【有typo？？】

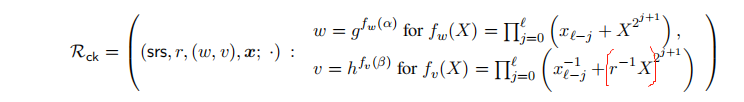
里面涉及2个polynomial：

• $f_w(X)=\prod_{j=0}^{l}(x_{l-j}+X^{2^{j+1}})$
• $f_v(X)=\prod_{j=0}^{l}(x_{l-j}^{-1}+(r^{-1}X)^{2^{j+1}})$

借助[KZG10] polynomial commitment来证明relation $\mathcal{R}_{ck}$成立，基本思路为：

• 1）Prover发送声称的evaluations $w,v$；
• 2）Verifier发送随机challenge $z$；
• 3）Prover 发送argument，用于convince the verifier if and only if $w$ and $v$ are correct。

详细算法实现如下图所示：

5.3 TIPP的计算复杂度

如5.2节所示：

• Prover SRS包含 $2m$ 个elements in $\mathbb{G}_1$ 和 $2m$ 个 $\mathbb{G}_2$。由于SRS中包含的都是monomials，因此支持updatable。
• Verifier SRS包含 $1$ 个element in $\mathbb{G}_1$ 和 $1$ 个 $\mathbb{G}_2$。
• 其它：