Subvector Commitments with Application to Succinct Arguments学习笔记

1. 背景知识

Russell W. F. Lai 和 Giulio Malavolta 在Crypto 2019上发表的论文《Subvector Commitments with Application to Succinct Arguments》中主要关注的是subvector commitment (SVC)：

• SVC允许open a committed vector at a set of positions，且opening size与vector的size以及要open的位置数均无关。
• subvector commitment based on root assumption (RSA assumption)，同时将其推广到work over modules over Euclidean rings。
• subvector commitment based on CubeDH assumption。
• Linear map commitment (LMC)：allow to open a committed vector to its images under linear maps with a single short message, and propose a construction over pairing groups。
• CS proof：使用Fiat-Shamir transform in the random oracle model 来构建non-interactive argument。
• 本文提出使用SVC来实现将PCP转换为non-interactive argument。
• 在该文第8章提出了一些可供被选定module families。

SVC可看成是支持batch opening和batch updating的VC。

Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》（参见博客 Vector Commitments and their Applications学习笔记）的算法无法实现reveal multiple locations of the committed vector（除非repeat the protocol in parallel，但是相应opening size会grow linearly with the amount of revealed locations。）。

Benoˆıt Libert, Somindu C. Ramanna 和 Moti Yung 2016年论文 《Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators from Simple Assumptions》（参见博客 Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators学习笔记）的算法无法实现reveal multiple function outputs （除非repeat the protocol in parallel，但是相应opening size会grow linearly with the amount of revealed function outputs。）。
从中可观察其open 单独位置时，其verification equation $e(C,U_{n-i+1})=e(G_1,U_n)^{m_i}\cdot e(g,W_i)$ 为 $m_i$的线性方程式，a natural way to support batching openings is to define the new verification equation as a random linear combination of previous ones。从而要求，在public parameters中嵌入a secret linear combination，and show that the resulting construction is function binding in the generic bilinear group model。

现有各方案对比（vector length为 $l$ ，open位置数为 $q$ ）

其中：

• public-coin setup 是指：Prover和Verifier之间不共享任何信息，除了the statement $x$ to be proven。（如基于CRH assumption和Root assumption的情况。）
• private-coin setup即pre-processing model：Prover和Verifier需共享由可信第三方生成的common reference string（该common reference string可能与language $L$ 和statement $x$相关。）。

目前的SNARK (succinct non-interactive argument of knowledge )方案，基于pre-processing model的方案，无论在communication还是在computation效率上，都要优于基于public-coin-setup 的方案。相当于，将verifier的一些工作转移给了offline preprocessing 阶段，从而减少整个online phase的工作量。
但在cryptocurrency等应用场景，则需要public-coin setup，可借助random oracle来实现public initialize。

1.1 public-coin-setup SNARK (Bulletproof)

在standard model下不存在public-coin-setup的non-interactive argument for NP，但是在random oracle model情况下可以存在。

通过“CS proof”(computationally sound proof) paradigm based on probabilistically checkable proof (PCP) 来构建public-coin-setup SNARK，分两步来实现：【通常，该argument system有public-coin verifier，且可利用Fiat-Shamir transform来实现non-interactive。】

• 将PCP转换为interactive argument system：Prover commit to the PCP string（通常使用Merkle-tree commitment）；Verifier 发送 the indices of the entries to be inspected；Prover open the commitment at these entries。【若为 $q$-query PCP，对应的inspect entries的个数最多为 $q$。】
• By inspecting the revealed entries, the verifier can decide whether the statement is valid。

根据Micali 1994年论文《CS proofs (extended abstracts)》可知，在CS proof paradigm中，a proof 的组成有：

• $\lambda$-bit Merkle-tree commitment of a $l$-bit PCP string；
• $q$ bits of the PCP string；
• $q$ openings of the commitment，each of size $\lambda\log l$ bits。

对于 $q$-query $2^{-\sigma}$-soundness PCP scheme, allows the prover to efficiently compute a PCP strign which encodes the witness of the sttement to be proven, the verifier can then decide wheteher the statement is true with probability close to $1-2^{-\sigma}$ by inspecting $q$ entries of the PCP string。
具体地，对于 $3$-query PCP and $l=2^{30}$, for $2^{-80}$-soundness against a $2^{128}$-time adversary, the proof size is around 113KB。

截止目前为止，Bulletproof 【主要论文为Jonathan Bootle等人2016年论文《Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting》和Benedikt Bunz、Jonathan Bootle等人2018年论文《Bulletproofs: Short proofs for confidential transactions and more》】为目前为止最使用的non-interactive argument，尽管Bulletproof具有linear verification time问题（因此不能称为SNARK）。Bulletproof中的proof有 $2\log n+13$ (group and field) elements, where $n$ is the number of multiplication gates in the arithmetic circuit representation of the verification algorithm of $L$。基于secp256k1实现的Bulletproof中，每个group element和integer可由 $\sim 256$ bits，所以整个proof 大约有 $512\log n+3328$ bits。

1.2 Pre-Processing SNARK

自Gennaro等人2013年论文《Quadratic span programs and succinct NIZKs without PCPs》起，有大量SNARK出现 based on pairings and linear interactive proofs (LIP) in pre-processing model。其中linear interactive proofs (LIP)可从linear PCPs中获得。
Linear PCP=传统PCP + encode PCP string in a linear form。在 $q$-query linear PCP中，Verifier可oracle access to the linear form，然后仅需 $q$ queries就可以以overwhelming probability来确定statement 的真实性。这种类型的SNARK存在的一个典型的问题为：需要有昂贵的pre-processing phase，且该pre-processing为statement-dependent的，意味着每证明一种statement，就需要建立相应的public parameters。
基于Danezis等人2014年论文《Square span programs with applications to succinct NIZK arguments》可构建standard model下具有最短proof（4 group elements）的SNARK。
而在generic bilinear group model情况下，Groth 2016年论文《On the size of pairing-based non-interactive arguments》中指出，基于LIP的SNARK proof至少具有2个group elements，同时proposed a scheme with only 3 group elements。该scheme可基于pairing-friendly elliptic curve来实现，比较流行的曲线有256-bit Barreto-Naehrig curve（每个group element 由256bit表示）等。

1.3 public-coin-setup SVC based on $Cl(\Delta)$

$Cl(\Delta)$表示：class group of imaginary quadratic order with discriminant $\Delta$。

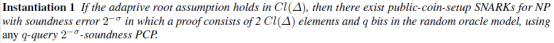
Prover的computation压力和proof的长度之间需要平衡：
若可接受expensive prover computation，追求extremely short proof，则可将 $3$-query $2^{-1}$-soundness PCP 放大为 $3\sigma$-query $2^{-\sigma}$-soundness PCP，实现shortest SNARK。Hamdy 2000年论文《Security of cryptosystems based on class groups of imaginary quadratic orders》中指出，based on the best known attacks on the root problem in class groups, for a soundness error of $2^{-80}$ against a $2^{128}$-time adversary, 可获得的proof size为5360 bits。【当 $n>16$时，其proof长度要短于Bulletproof。】

1.4 pairing-based public-coin-setup SVC

如Bitansky等人2013年论文《Succinct non-interactive arguments via linear interactive proofs》中基于pairing group over 256-bit Barreto-Naehrig curve可实现5 elements（1280 bits）的proof。
与Groth 2016年论文《On the size of pairing-based non-interactive arguments》相比，本论文构建的compiler可支持任意linear PCPs，且不要求verifier仅能evaluate quadratic polynomials。
现有各方案的对比：

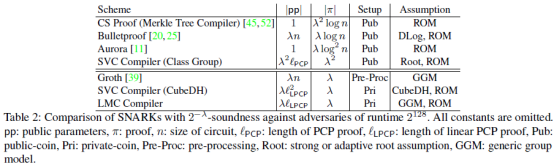
而且本论文的setup phase与待证明的statement无关，所以相同的public parameters可重复用于证明不同的statement。
通过a higher prover complexity和使用密码学public-key技术，本问可实现更短的proof，同时支持更广类型的PCP（与schemes under the CS proofs paradigm和pairing-based schemes相比）。

SVC为当前社区关注的热点，Boneh等人2018年论文《Batching techniques for accumulators with applications to iops and stateless blockchains》展示的是how SVCs can be used as a drop-in replacement for Merkle-trees in SNARKs based on interactive oracle proofs(IOPs) which generalizes PCPs，利用class group-based SVCs 结构reduce the proof size to $(r+1)$ group elements and $r$ integers，其中 $r$ 表示 the number of iterations of the underlying IOP。Boneh还提出了可用于提高verification algorithm效率的方法，预计可将verification time下降约 $80$，并指出可使用SVC来改进the current design of blockchain-based transaction ledger in such a way that no user has to store the entire state of the ledger in memory。

Benoˆıt Libert, Somindu C. Ramanna 和 Moti Yung 2016年论文《Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators from Simple Assumptions》中实现了accumulator for subset query（参见博客 Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators学习笔记 5.3节内容“Functional commitment构建支持subset query的accumulator”），与SVC最大的不同是不具有position binding属性。

1.5 一些定义

• subvector 定义：
  

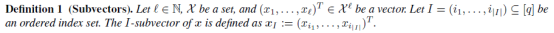
• argument of knowledge定义：
  

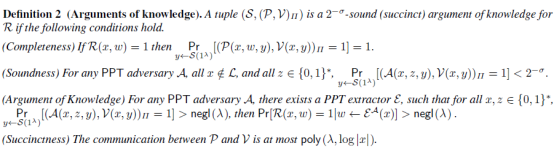
• probabilistic checkable proof (PCP) 定义：
  

• proof of knowledge 定义：
  

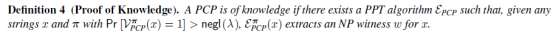
• linear PCP 定义：
  

• 数学背景知识：
  

• (Public-Coin) Adaptive Root 定义：
  
  即(Public-Coin) Adaptive Root可概括为：已知 $e$和 $X$值，求相应的 $Y$值使得 $e\circ Y=X$成立的概率可忽略。

• (Public-Coin) Strong Distinct-Prime-Product (Divisible) Root 定义：
  
  即Strong Distinct-Prime-Product (Divisible) Root可概括为：不存在co-prime $(e_1,\cdots,e_l)$和 $Y$，使得 $A$可分解表示为 $(\prod_{i\in S}e_i)\circ Y$。

• subvector commitment 定义：
  

• Linear Map Commitments (LMC) 定义：
  

2. subvector commitment (SVC)

subvector commitment (SVC) 定义为：
commit to a vector $\vec{x}$ of length $l$，然后允许open to a subvector of an arbitrary length $\leq l$。
Given an ordered index set $I\subseteq [l]$, define the $I$-subvector of $\vec{x}$ as the vector formed by collecting the $i$-th component of $\vec{x}$ for all $i\in I$。

2.1 SVC succinct

SVC应succinct：

• commitment size与vector length $l$ 无关；
• opening proof size与vector length $l$ 无关；
• opening proof应具有compactness，其size应与要open的位置数 $q$ 无关。

本文将SVC的概念归纳为 linear map commitments (LMC)，即：
允许prover reveal arbitrary linear maps $f:\mathbb{F}^l\rightarrow\mathbb{F}^q$ computed over the committed vector。

为满足SVC的succinct特性，相应地要求LMC为be compact，其commitment size和proof size与 $l$ 和 $q$ 均无关。SVC看做LMC的话，要求linear map 可以矩阵表示，该矩阵内每行只有一个 $1$，其它均为 $0$。

2.2 SVC function binding

function binding为position binding的加强版。
直观的，对于position binding，以LMC表示时，Prover cannot open a commitment to $(f,\vec{y})$ and $(f,\vec{y}^{'})$ with $\vec{y}\neq\vec{y}^{'}$，其中 $f$ 为linear map， $\vec{y},\vec{y}^{'}\in{\mathbb{F}^k}$ 为vectors。
仅如上一条约束仍然不够，Prover 通过form an inconsistent system of linear equations的方式，可能存在open to $(f,\vec{y})$ and $(f^{'},\vec{y}^{'})$ with $f\neq f^{'}$ and $\vec{y}\neq\vec{y}^{'}$。

从而要求SVC应具有function binding 属性：
no efficient algorithm can produce openings for $Q$ function-value tuples $\{(f_k,\vec{y}_k)\}_{k\in[Q]}$ for any $Q\in poly(\lambda)$, such that there does not exist $\vec{x}$ with $f_k(\vec{x})=\vec{y}_k$ for all $k\in [Q]$。【即要求open $Q$组信息时，不存在统一的 $\vec{x}$满足所有open linear function $f_k$。】

3. subvector commitment based on root assumption over Euclidean ring

具体实现如上图所示。
其中：

• $(e_1,\cdots,e_l)$为 $l$ 个不同的co-prime素数。
• setup阶段的 $S_i$构建方式为： $S_i=(\prod_{j\in [l] \setminus \{i\}}e_j) \circ X=(\prod_{j\in I}e_j \prod_{j\in [l] \setminus (I\cup \{i\})}e_j) \circ X$。【由于 $(e_1,\cdots,e_l)$为distinct co-prime，从而使得计算的 $S_i$具有position binding属性。】
• setup阶段的 $H$可为：
  1）non-cryptographic hash：secure if the strong distinct-prime-product root assumption hold over the module family $R_D$。
  2）random oracle：secure if the adaptive root problem is hard over the module family。
• open阶段的proof： $\Lambda_I=(\prod_{i\in I}e_i)^{-1}\circ <\vec{x}_{[l]\setminus I}, \vec{S}_{[l]\setminus I}>$
• Verify阶段，基于adaptive root assumption，除非Prover真的知道相应的witness $\vec{x}$ 从而提供正确的 $\Lambda_I$值，否则等式 $C=<\vec{x}_I^{‘},\vec{S}_I>+(\prod_{i\in I} e_i)\circ \Lambda_I$成立的概率可忽略。

4. subvector commitment based on CubeDH assumption over pairing group

为便于描述，采用的是对称pairing group来示例，如上图所示。
其基本实现思路与Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》中的“基于CDH的Vector Commitment实现”类似——基于的是Square-CDH assumption：已知 $g,g^{a}\in\mathbb{G}$，要计算 $g^{a^2}$的值为computationally infeasible。（参见博客 Vector Commitments and their Applications学习笔记 第2.1节内容）

不同之处在于：

• 为了支持batch open和batch verify，相应的计算由“ $\Lambda_i=\prod_{j\in [l], j\neq i}H_{i,j}^{x_j}$，验证 $e(C/G_i^{x_i},G_i)=e(\Lambda_i,G)$成立”，改为，“对集合 $I$的batch open $\Lambda_I=\prod_{i\in I}\prod_{j\in [l],j\notin I}H_{i,j}^{x_j}$，batch verifiy $e(\frac{C}{\prod_{i\in I}G_i^{x_i}},\prod_{i}G_i)=e(\Lambda_I,G)$”。
• 为了实现多个位置的position binding属性（即batch open & batch verify）， 本论文基于的为cube Diffie-Hellman (CubeDH) assumption：已知 $g,g^{a}\in\mathbb{G}$，要计算 $g^{a^3}$的值为computationally infeasible。在该论文中的Theorem 3中采用了归谬法的方式来证明，若对交集位置可open为不同的值，则需要知道相应的 $g^{a^3}和g^{a^2}$。
  
  

5. linear map commitment (LMC) 的构建

本文LMC的构建方式收到Benoˆıt Libert, Somindu C. Ramanna 和 Moti Yung 2016年论文 《Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators from Simple Assumptions》启发，并基于以下观察：

• 当vectors $\vec{x},\vec{f}\in\mathbb{F}^l$ 分别采用多项式 $p_{\vec{x}}(\alpha)=\sum_{j\in [l]x_j\alpha^j}$和 $p_{\vec{f}}(\alpha)=\sum_{j\in [l]}f_j\alpha^{l+1-j}$来编码，则多项式乘积$p_{\vec{x}}(\alpha) p_{\vec{f}}(\alpha) $ 生成的多项式中 $\alpha^{l+1}$ 项的系数为 $<\vec{x}, \vec{f}>$（inner product）。
• 因多项式乘积具有linearity，对矩阵 $F\in\mathbb{F}^{q\times l}$可用多项式 $p_F(\alpha)=\sum_{i\in q,j\in [l]}f_{i,j}z_i\alpha^{l+1-j}$（参数为 $(\alpha,z_1,\cdots,z_q)$）编码，则多项式乘积 $p_F{\alpha}p_{\vec{x}}(\alpha)$生成的多项式中 $z_i\alpha^{l+1},\ for\ i\in [q]$项的系数即为相应的矩阵与vector乘积 $F\vec{x}$。
  利用commitment的加法同态性，可利用public parameters $G^{\alpha^j}$来commit to $\vec{x}$ be $G^{p_{\vec{x}}(\alpha)}$，矩阵 $F$ 为public info（对Prover和Verifier均已知），则batch open的过程可基于 $F\vec{x}=\vec{y}$来生成proof【即the coefficients of $\vec{y}$ must be encoded as the coefficients as the (lifted) monomials $G^{z_i\alpha^{l+1}}$】。详细的流程为：
  

6. 构建succinct arguments of knowledge from SVC/LMC

可通过“traditional PCP + SVC“ 或 ”linear PCP + LMC“ 来构建4-move interactive arguments of knowledge：

其中的Record、Reconstruct和Decide算法含义为：