支持向量机(SVM)的算法原理，公式推导，python编程实现

1.前言

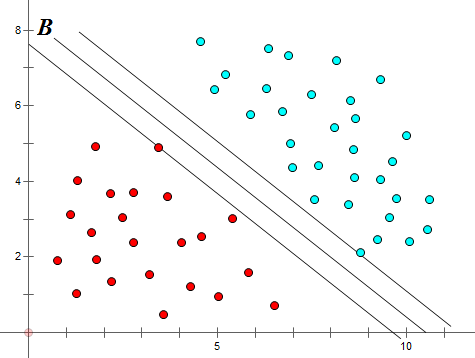
如图，对于一个给定的数据集，通过直线A或直线B（多维坐标系中为平面A或平面B）可以较好的将红点与蓝点分类。那么线A与线B那个更优呢？

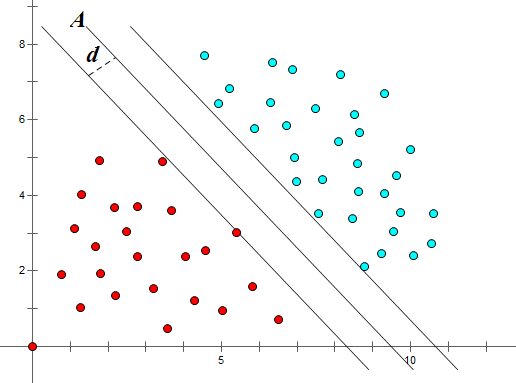
在SVM算法中，我们认为线A是优于线B的。因为A的‘分类间隔’大于B。

那么什么是分类间隔呢？以A线所在图为例，平移直线A直到找到一个极限位置，越过该位置，就会产生分类错误的现象。如图，直线A左右两边的直线就是所谓的极限位置，再往左或者往右移动一下直线都会出现分类错误的情况。这2条直线之前的垂直距离就是分类间隔。（2d）

而这2条直线中间的分界线也是分类间隔中心所在的直线就是SVM的‘最优决策面’

而这两条直线上面的点，我们称之为‘支持向量’

通俗一点来说，SVM的分类目的就是找到最大的分类间隔即使得2倍的d最大。

2.SVM的最优化问题

首先回顾一下初中便开始接触的知识：

对于求坐标系中任意点 $\small \bg_white \small (x^{i},y^{i})$ 到直线 $\small Ax+By+C=0$ 的距离，我们很容易给出下面的式子：

$\small d=\frac{\left | Ax^{i}+By^{i}+C \right |}{\sqrt{A^{2}+B^{2}}}$

把这个原理应用在N维的空间会怎样？首先N维空间的曲线我们可以用一个我们熟知的式子来表示：

$\small W^{T}x+b=0$

那么空间中任意一点到曲线的距离可以表示为：

$\small d=\frac{\left | W^{T}x^{i}+b\right |}{\left \| W \right \|}$

其中： $\small \left \| W \right \|=\sqrt{w_{1}^{2}+w_{2}^{2}+w_{3}^{2}+....+w_{n}^{2}}$ 。

我们令左侧的数据的类别为-1，及对应决策平面左侧的点 $\small y^{i}=-1$ 。同理，右侧的点为+1， $\small y^{i}=1$ 。

你不用去在意为什么是-1和1，实质上你可以令其为任何你想的数，只是用1和-1会在之后的计算中更为简便一些。

那么决策平面A左右2侧的极限位置外的点我们就可以这样表示：

$\bg_white \large \left\{\begin{matrix} \frac{\left | W^{T}x^{i}+b\right |}{\left \| W \right \|}\geq d& y^{(i)}=1\\ \frac{\left | W^{T}x^{i}+b\right |}{\left \| W \right \|}\leq -d& y^{(i)}=-1\end{matrix}\right.$

移项：

$\bg_white \large \left\{\begin{matrix} \frac{\left | W^{T}x^{i}+b\right |}{\left \| W \right \|d}\geq 1& y^{(i)}=1\\ \frac{\left | W^{T}x^{i}+b\right |}{\left \| W \right \|d}\leq -1& y^{(i)}=-1\end{matrix}\right.$

我们令

$\frac{W^{T}}{\left \| W \right \|d}=W^{T}_{d}$ $\frac{b}{\left \| W \right \|d}=b_{d}$

那么原式就可以转化为：

$\left\{\begin{matrix}\left | W^{T}_{d}x^{i}+b_{d}\right |\geq 1& y^{(i)}=1\\ \left | W^{T}_{d}x^{i}+b_{d}\right |\leq -1& y^{(i)}=-1\end{matrix}\right$

对于决策平面A我们也可以用同样的方式表示：

$\small W^{T}_{d}x^{i}+b_{d}=0$

这里有个技巧性的办法，因为我们之前令 $\small y^{i}=+1 /-1$ 。那么上式也可以转化为：

$y^{(i)}[ W^{T}_{d}x^{i}+b_{d}] \geq 1$

为了之后的便于书写，通常情况下，在这个时候，我们会直接设

$W^{T}_{d}=W^{T}$ $b_{d}=b$

*这里的 $W^{T}$ 与 $b$ 与之前的 $W^{T}$ ， $b$ 是不同的概念，相差了一个系数 $\frac{1}{\left \| W \right \|d}$ 的关系，这样做也是为了便于书写，这些是约定俗成的

*记住在这之后的 $W^{T}$ 与 $b$ 都是 $\frac{W^{T}}{\left \| W \right \|d}$ , $\frac{b}{\left \| W \right \|d}$

这样之后

$\left\{\begin{matrix}\left | W^{T}_{d}x^{i}+b_{d}\right |\geq 1& y^{(i)}=1\\ \left | W^{T}_{d}x^{i}+b_{d}\right |\leq -1& y^{(i)}=-1\end{matrix}\right$

$\small W^{T}_{d}x^{i}+b_{d}=0$

$y^{(i)}[ W^{T}_{d}x^{i}+b_{d}] \geq 1$

就转化为了

$\left\{\begin{matrix}\left | W^{T}x^{i}+b\right |\geq 1& y^{(i)}=1\\ \left | W^{T}x^{i}+b\right |\leq -1& y^{(i)}=-1\end{matrix}\right$

$\small W^{T}x^{i}+b=0$

$y^{(i)}[ W^{T}x^{i}+b] \geq 1$

所以我们求最大分割间隔的长度问题就可以表示为：

$\small max(2d)=max(\frac{2\left | W^{T}x^{i}+b\right |}{\left \| W \right \|})$

而我们知道决策平面平移的极限条件为 $y^{(i)}[ W^{T}x^{i}+b] =1$ ，所以：

$\small max(2d)=max(\frac{2\left | W^{T}x^{i}+b\right |}{\left \| W \right \|})=max(\frac{2}{\left \| W \right \|})=min(\frac{1}{2}\left \| W \right \|)$

通常情况下我们不会去求 $\small min(\frac{1}{2}\left \| W \right \|)$ 而是转而去求 $\small min(\frac{1}{2}\left \| W \right \|^{2})$ 的值，这实质上也是为了计算方便，但是从理论上上两者结果并无差别。

我们梳理一下重点内容，通过上面的推到，我们把一个分类的问题转化为了一个最优化问题，

$min(\frac{1}{2}\left \| W \right \|^{2})$

${\color{Red} s.t.}y^{(i)}[ W^{T}x^{i}+b] \geq 1$ （ ${\color{Red} s.t.}$ 表示的是限定的条件）

3.解决SVM最优化问题

上一节我们由分类间隔的思想得到一个最优化问题。这节将以纯数学的方式和大家一起解决这个最优化问题。

首先需要为大家介绍一下，拉格朗日算子。

百度百科：
在数学最优化问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。

拉格朗日算子的定义是生涩不易懂的，所以这里我将用一个例题来让对SVM中拉格朗日算子的作用有更深刻的认识：

例：给定椭球 $\bg_white \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1$ ，求这个椭球的内接长方体的最大体积，即 $f(x,y,z)=8xyz的最大值$ 的最大值

解：建立拉普拉斯算式，算式的偏导为0

$\bg_white f(x,y,z)=8xyz+\lambda(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1)$

$f(x,y,z)$ 对 $x,y,z$ 的偏导结果为0

$\large \left\{\begin{matrix} \frac{\partial f(x,y,z)}{\partial x}=8yz+\frac{2\lambda x}{a^2}=0\\ \frac{\partial f(x,y,z)}{\partial y}=8xz+\frac{2\lambda y}{b^2}=0\\ \frac{\partial f(x,y,z)}{\partial z}=8xy+\frac{2\lambda z}{c^2}=0\\ \frac{\partial f(x,y,z)}{\partial \lambda }= \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1=0\end{matrix}\right.$

联立四个方程：

$\left\{\begin{matrix} bx=ay\\cy=bz\\az=cx \end{matrix}\right.$

代入 $\bg_white \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1$ ：

$\left\{\begin{matrix} x=\frac{\sqrt{3}}{3}a\\y=\frac{\sqrt{3}}{3}b\\z=\frac{\sqrt{3}}{3}c\end{matrix}\right.$

于是得到：

$max(f(x,y,z))=\frac{8\sqrt{3}}{9}abc$

同样以拉格朗日的算子的原理来求解我们SVM分类的最优化问题：

$min(\frac{1}{2}\left \| W \right \|^{2})$

${\color{Red} s.t.}y^{(i)}[ W^{T}x^{i}+b] \geq 1$ （ ${\color{Red} s.t.}$ 表示的是限定的条件）

由拉格朗日算子定义可以转化成：

$L(w,b,x_{i})=\frac{1}{2}\left \| w \right \|^{2}-\sum _{i=1}^{n}\alpha _{i}(y^{(i)}[ W^{T}x^{i}+b]-1)$

其中 $L(w,b,x_{i})$ 对 $w,b$ 的偏导为0

$\large \left\{\begin{matrix} \frac{\partial L(w,b,x_{i})}{\partial w}=w-\sum_{i=1}^{n}\alpha _{i}x^{(i)}y^{(i)} =0\\ \frac{\partial L(w,b,x_{i})}{\partial b}=\sum_{i=1}^{n}\alpha_{i}y^{(i)}=0\end{matrix}\right.$

得到结果：

$\large w=\sum_{i=1}^{n}\alpha _{i}x^{(i)}y^{(i)}$ $\large \sum_{i=1}^{n}\alpha_{i}y^{(i)}=0$

将这2个结果代入 $L(w,b,x_{i})$ ：

$L(w,b,x_{i})=$

$\small =\frac{1}{2}\sum_{i=1}^{n}\alpha _{i}x^{(i)}y^{(i)}\sum_{j=1}^{n}\alpha _{j}x^{(j)}y^{(j)}-\sum_{i=1}^{n}\alpha _{i}x^{(i)}y^{(i)}\sum_{j=1}^{n}\alpha _{j}x^{(j)}y^{(j)} -\sum_{i=1}^{n}\alpha_{i}y^{(i)}b+\sum_{i=1}^{n}\alpha_{i}$

$\bg_white \small \dpi{100} \small =\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y^{(i)}y^{(j)}x^{(i)}x^{(j)}$

所以我们的最优化问题就转化为了：

$\large \bg_white \small max[\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y^{(i)}y^{(j)}x^{(i)}x^{(j)}]$

${\color{Red} s.t.}\sum_{i=1}^{n}\alpha_{i}y^{(i)}=0$

$0\leq \alpha_{i}\leq C$

4.SVM的核函数

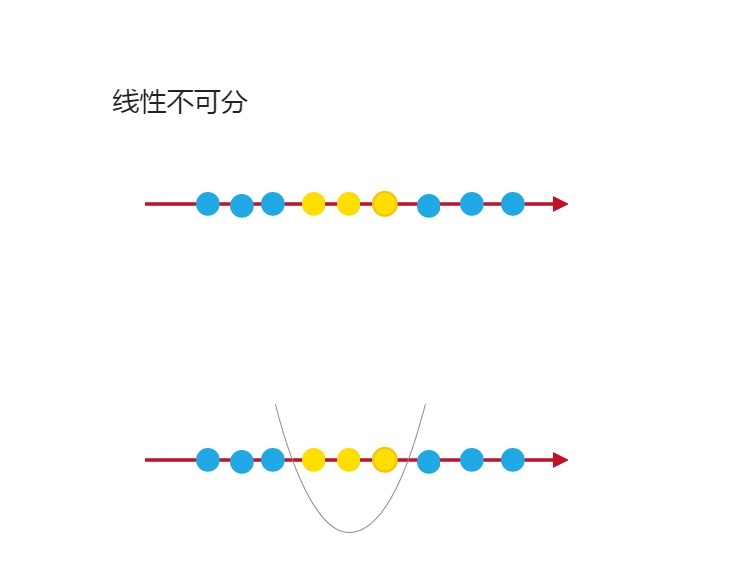
在第三节中，我们将最优化问题使用拉格朗日算子进行了转化，在这一小节要介绍的是SVM的核函数，了解SVM是怎么通过核函数减少欠拟合和过拟合现象的。

首先观察式子 $\large \bg_white \small max[\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y^{(i)}y^{(j)}x^{(i)}x^{(j)}]$

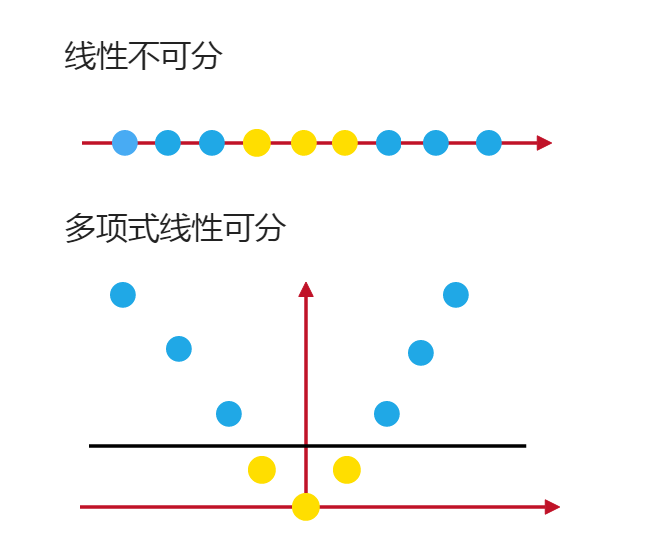
发现这个式子会对每个 $\large x^{(i)},x^{(j)}$ 进行点乘，现在我们将 $\large x^{(i)},x^{(j)}$ 添加上多项式特征使其得到更为复杂的分割曲线：

我们设具有多项式特征的 $\large x^{(i)},x^{(j)}$ 表示为 $\large x^{'(i)},x^{'(j)}$ ,现在假设，我们找到一个函数使得：

$\large K(x^{(i)},x^{(j)})=x^{'(i)},x^{'(j)}$

那么求解具有多项式特征的SVM分类器的最优化问题就转化为：

$\large \bg_white \small max[\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y^{(i)}y^{(j)}K(x^{(i)},x^{(j)})]$

而这个函数 $\large K(x^{(i)},x^{(j)})$ 就是所谓的核函数：

如果不使用核函数，那么我们需要先将 $\large x^{(i)},x^{(j)}$ 转化为 $\large x^{'(i)},x^{'(j)}$ 然后再将 $\large x^{'(i)},x^{'(j)}$ 代入最优化式子去求解。而设定这个核函数就是为了直接将 $\large x^{(i)},x^{(j)}$ 代入最优化式子求得多项式最优解。这样减少了部分计算机计算开销和存储开销。

从这一点可以看出核函数并不是SVM的专用方法，实质上在我们求解最优化问题上遇到 $\large x^{(i)}$ 点乘 $\large x^{(j)}$ 的时候，我们都可以使用到核函数这种技巧。

4.0线性核函数：

$\bg_white \large \dpi{100} \large K(x,y})=x\cdot y$

4.1多项式核函数（poly）：

$\large \dpi{100} \large K(x,y})=(x\cdot y+c)^{d}$

我们以2次项为例子,如果我们直接算 $\large K(x_{i},y_{i})=x^{'}y^{'}$ ，我们需要下面这个几个步骤：

$\large K(x_{i},y_{i})=(\sum _{i=1}^{n}x_{i}x_{i}+1)^{2}$

$\large =\sum _{i=1}^{n}x_{i}^{2}y_{i}^{2}+\sum _{i=2}^{n}\sum _{j=1}^{i-1}(\sqrt{2}x_{i}x_{j})(\sqrt{2}y_{i}y_{j})+\sum _{i=1}^{n}\sqrt{2}x_{i}\sqrt{2}y_{i}+1$

$\large =x^{'}y^{'}$

通过上面这个式子，我们可以直接理解为我们将原来的 $\large x$ 转化成了

$\large x^{'}=(x^{2}_{n}...x^{2}_{1},\sqrt{2}x_{n}x_{n-1}.....\sqrt{2}x_{2}x_{1},\sqrt{2}x_{n}....\sqrt{2}x_{1},1)$

而使用到核函数这种方法，我们就直接将x,y带入 $\large K(x,y})=(x\cdot y+1)^{2}$ ，这种方式大大的降低了我们计算的复杂度。

回到这个我们最优化问题中：

$\large \bg_white \small max[\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y^{(i)}y^{(j)}K(x^{(i)},x^{(j)})]$

我们只用将 $\large K(x,y})$ 替换成 $\large (x\cdot y+1)^{d}$ ，就为其添加了多项式的特征。其实应该为 $\large (x\cdot y+c)^{d}$ 这个C为正则化的系数。

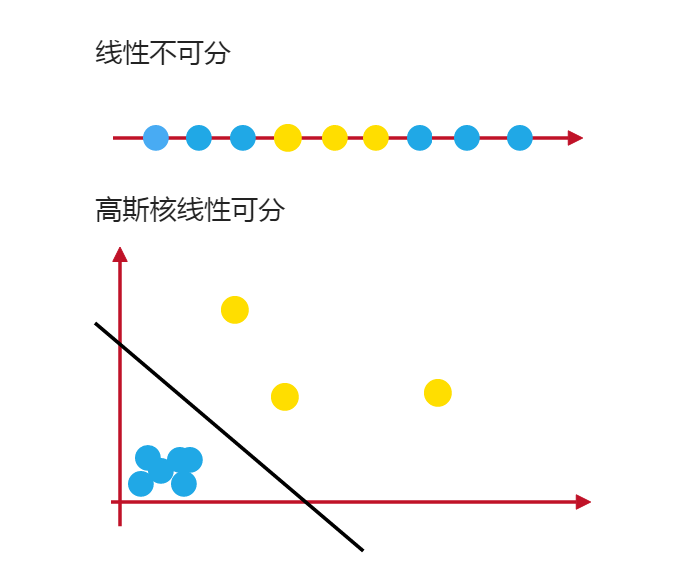
4.2高斯核函数（rbf）：

$\bg_white \large \dpi{100} \large K(x,y})=e^{-\gamma \left \| x-y \right \|^{2}}$

首先我们介绍下高斯函数：

$\large g(x)=\frac{1}{\sigma \sqrt{2\pi }}e^{-\frac{1}{2}(\frac{x-\mu }{\sigma})^{2}}$

高斯核的转化方式如上图：双曲线与坐标轴的交点为 $l_{1},l_{2}$

$\bg_white \large x\rightarrow (e^{-\gamma \left \| x-l_{1} \right \|^{2}},e^{-\gamma \left \| x-l_{2} \right \|^{2}})$

关于高斯核函数的解释我使用可视化的方式我觉得这样可以方便理解：使用工具python的numpy和matpoltlib

import numpy as np
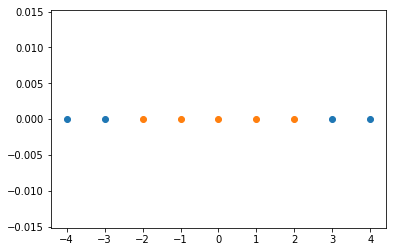
import matplotlib.pyplot as plt

#定义一个从-4到5分布的数值，分割间隔为1
In [1]:x=np.arange(-4,5,1)
Out[1]: array([-4, -3, -2, -1,  0,  1,  2,  3,  4])
#将-2到2之间的点归为一类，类别为1，将小于-2和大于2的点归为一类，类别为0
In [2]:y=np.array((x>=-2)&(x<=2),dtype='int')
Out[2]: array([0, 0, 1, 1, 1, 1, 1, 0, 0])

#可视化一下
plt.scatter(x[y==0],[0]*len(x[y==0]))
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

#定义高斯核的公式：
def gaussian(x,l):
    gamma=1.0
    return np.exp(-gamma * (x-l)**2)

#定义L1和L2的值，即分类的边界点
l1 , l2 = -1, 1
#开辟一个新的空间，用于存放之后计算出来的额高斯值
new_x = np.empty((len(x),2))
#将x中的每个值代入高斯核函数中
for i,data in enumerate(x):
    new_x[i,0] = gaussian(data, l1)
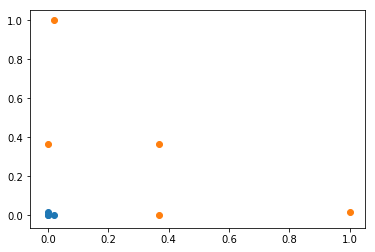
    new_x[i,1] = gaussian(data, l2)

#可视化一下代入高斯核函数后的x分布情况
plt.scatter(new_x[y==0,0],new_x[y==0,1])
plt.scatter(new_x[y==1,0],new_x[y==1,1])
plt.show()

从可视化的图形可以看出，经过高斯核函数后的x变得线性可分了。

打赏一下作者：