共生矩阵及其描述子 Texture Descriptors
1 共生矩阵及其描述子的计算
1.1 共生矩阵原理及其描述子表达式
共生矩阵统计了灰度图中像素间的灰度值分布规律,并借此区分不同的纹理。 灰度共生矩阵中每个元素的值可以定义为(x,y)点与(x+dx,y+dy)点的值对为(i,j)的概率。统计整幅图像中每一种灰度值组合出现的概率矩阵 P 即为灰度共生矩阵。参考实验PPT中助教给的实例来解释共生矩阵,如图所示:

这里考虑的是水平方向的共生矩阵的结果。具体来看,由于(1,1)只出现1次,所以共生矩阵第一行第一列为 1;(6,2)出现3次,所以共生矩阵第六行第二列为 3,以此类推,直到将所有的结果就算出来,便可得到上图右部分所示的共生矩阵。
基于 (归一化后的) 共生矩阵,我们可以计算共生矩阵很多参数。本次实验中要求计算以下六个参数,分别是最大概率(Maximum Probability)、相关性(Correlation)、对比度(Contrast)、一致性(Uniformity(Energy))、同质性(Homogeneity)以及熵(Entropy)。这六个参数定义如下。
最大概率(Maximum Probability):
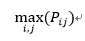
相关性(Correlation):
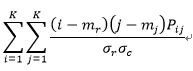
对比度(Contrast):

一致性(Uniformity(Energy)):

同质性(Homogeneity)
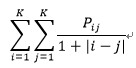
熵(Entropy)
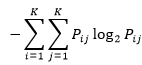
我们统一将上面六个参数成为描述共生矩阵的描述子。
1.2 实验结果
在助教给的 G1,G2,G3 三张图片上进行了实验。所得到的共生矩阵以及对应的共生矩阵描述子如下:
首先是图G1的,原图(左)和共生矩阵(水平)(右)的图像如下图所示:


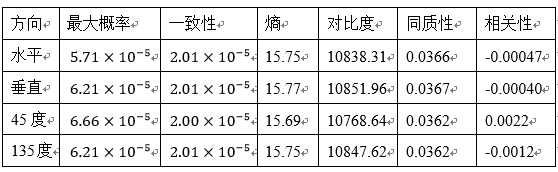
其对应的共生矩阵描述子如下表:
接下来是图G2的,原图(左)和共生矩阵(水平)(右)的图像如下图所示:


其中方向为垂直的共生矩阵的图像如下图所示:

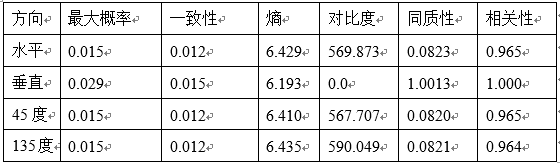
其对应的共生矩阵描述子如下表:
接下来是图G3的,原图(左)和共生矩阵(水平)(右)的图像如下图所示(共生矩阵的图片显示结果与书上的不同,会在1.3小节说明原因):


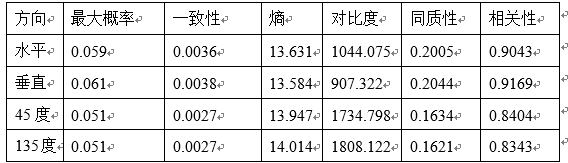
其对应的共生矩阵描述子如下表:
1.3 实验结果分析与结论
首先分析共生矩阵。对于图G1,其表示随机噪声,所以我们得到的共生矩阵也是较为随机的“噪音图像”;G原图是水平上的周期图像,或者说是空间上的正弦波。正弦波具有对称性,也就是说像素对(zi,zj)和像素对(zj,zi)的计数相同,这在G2共生矩阵中得到了体现(即G2共生矩阵是关于主对角线对称的),尤其是当我求不同方向的共生矩阵时,有比较明显的差距。同时,由于原图水平相邻像素的差值相对较小,数字化后正弦波是阶梯状的,这也导致 G2 的共生矩阵非零元素是稀疏且离散的;G3的结构是比较复杂的,因为是一幅可以表达真实场景的图像,所以相邻像素之间的灰度很少有较大的跳变,元素之间并不存在特别强的联系。这也就导致G3图像的共生矩阵在对角线上的数值都比较大(图像较平滑)。不过看到我的代码运行出的共生矩阵的“图像”,基本上是全“黑色”,这主要是因为,为了“画出”共生矩阵,这里我将所有的pixel都归一化到了0-255,而由于共生矩阵之间的极大值比较大,导致了归一化后的除了几个比较大的数值外的其他数值都归一化到了接近于0的值,所以不经过处理的话,共生矩阵显示的就是“全黑色”。同时,图G3中也存在几个由较小灰度跳变到较大灰度的区域,但跟整体相比,这些区域所占比重太小,因此在共生矩阵中没有体现。
其次是共生矩阵的描述子等指标情况。对于G1、G2、G3这三张图来说,最大概率最高的图是G3,最低的图是G1,这是符合预期的,因为 G3 的灰度值有着丰富的变化,相邻像素之间的灰度很少有较大的跳变,而图G1是“随机噪音”的图像,所以最大概率自然比较低。相关性最高的原图是 G2,这是因为 G2 是周期的,是反复出现的正弦模式,因为图G1是随机的噪音,所以其相关性接近于0。由此可知,相关性这个参数可以表示图像pixel的随机性能,图像随机性越大,图像的相关性越小。对于对比度指标来说,结果最高的是 G1,最低是 G2,可以判断出结论,图像的随机性越小,它的对比度往往也越小。同样的,图像的一致性会随着随机性的减小而增大,一致性中G2的数值是最高的,G1的数值是最低的。对于同质性,观察定义,我们可以知道同质性是在度量共生矩阵关于主对角线的集中度。可以发现 G3 的同质性最大, 这和观测到的共生矩阵是吻合的。图像的熵会随着随机性增大而增大,所以图G1的熵是最大的,G2的熵是最小的,此与熵的性质一致。
2 不变矩的计算
2.1 不变矩原理及计算公式
几何矩是由Hu(Visual pattern recognition by moment invariants)在1962年提出的,具有平移、旋转和尺度不变性的图像特征。
在连续情况下,图像函数为f(x,y) ,那么图像的p+q阶几何矩(标准矩)定义为:

其中p=0,1,2,…和q=0,1,2…是整数。相应的p+q阶中心矩定义为
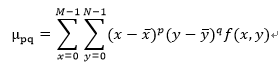
式中p=0,1,2,…和q=0,1,2…,其中
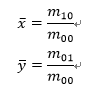
由μ_pq表示的归一化中心矩定义为

式中,
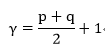
其中p+q=2,3,…
由二阶矩和三阶矩可推出如下的7个不变矩组:

其中ϕ_7中书上的公式有问题,感谢微信群里的同学的分享。以上矩组对于平移、尺度变化、镜像(第七个矩阵为负号)和旋转是不变的。
2.2 实验结果
实验的六张图片如下图所示,其中M1是原图、M2是平移后的图像、M3是缩小一半后的图像、M4是镜像后的图像、M5是旋转45度的图像、M6是旋转90度的图像。

为了减小动态范围进而简化解释,这里所显示的值是计算得到的不变矩ϕ_i经过如下计算的数值:
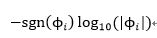
其中需要绝对值的原因是,许多值是小数或负数;符号函数的作用是保留符号(这里我们感兴趣的是矩的不变性和相对的符号,而不是它们的真实数值)
通过计算,最终得到的不变矩结果如下表:

2.3 实验结果分析与结论
从2.2的表格中我们可以看出,(1)7组不变矩的值的接近程度,与平移、尺度缩放、镜像和旋转无关;(2)φ_7的符号对于镜像图像是不同的,所以我们也可以根据这一点来在实践中检测一幅图像是否已被镜像。
使用不变矩我们可以对于图片进行识别,即识别由Hu矩组成的特征量。不过对于纹理比较复杂的图片,使用不变矩方法进行识别时,效果并不好,因为Hu不变矩只用到低阶矩(最多也就用到三阶矩),对于图像的细节未能很好的描述出来,导致对图像的描述不够完整,所以可能会导致识别效果变差。
网上的资料显示,Hu不变矩一般用来识别图像中大的物体,对于物体的形状描述得比较好,图像的纹理特征不能太复杂,像识别水果的形状,或者对于车牌中的简单字符的识别效果会相对好一些。
3 实验心得
通过本次上机实验,我了解了用于对于纹理描述的两个重要概念:共生矩阵和不变矩,并进行了代码实现。实验过程中主要遇到了两个问题:(1)在不变矩的公式中,书上的公式有问题,经过微信群的同学们分享正确公式以后才将最终的结果运行出来。(2)在不变矩的实验中,我又一次忘记了将uint8型图片和double类型图片的区别,导致一开始的不变矩的计算结果与书上的结果差距很大。吃一堑,长一智。