背包问题 (Knapsack problem) 是一种组合优化的 NP 完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。

本文主要介绍最常见的 01 背包问题，且只介绍动态规化的解法。

1. 基本题目描述与分析

问题描述

现有 $N$ 件物品和一个容量为 $C$ 的背包。放入第 $i\ (1\dots N)$ 件物品耗费的空间是 $w_i$ ，得到的价值是 $v_i$ 。求解将哪些物品装入背包可使价值总和最大。

之所以叫做 “0-1” 背包是因为在这里，每个物件只有一个。如果我们把 $\vec{x}$ 视为解空间中的某一个解，那么可以这么来表述:

$x_i = \begin{cases} &&0 &\text{第 i 件物品未放入背包}\\ &&1 &\text{第 i 件物品被放入背包} \end{cases} \quad i = 1, 2,\dots, N$

这个问题的形式化描述如下:

$\max_{\vec{x}}\sum_{i=1}^N{v_ix_i}\\ \text{s.t.} \left\{ \begin{aligned} &\sum_{i=1}^N{w_ix_i} \leqslant C\\ &x_i \in \{0, 1\}\ (1\leqslant i \leqslant N) \end{aligned} \right.$

分析

为了使用动态规化，我们首先定义目标函数 $F(i,\ c)$ ，它表示前 i 个物品放入容量为 c 的背包里最大的收益价值为多少。

首先我们只考虑前 i 个物品放入容量为 c 的背包里收益价值可以有多少，它可以分为两种情况:

把物品 i 放入背包中，则价值为 $F(i - 1,\ c - w_i) + v_i$
不把物品 i 放入背包中，则价值为 $F(i - 1,\ c)$

而 $F(i,\ c)$ 应当取这两者的较大值。

不过我们上面的考虑有一个疏漏，没有考虑到物品 i 放不进去的情况，在这种情况下 $F(i,\ c) = F(i - 1,\ c)$ 。

再考虑初始状况，则有:

$\begin{cases} F(0,\ 1\dots C) = 0\\ F(1\dots N,\ 0) = 0\\ \end{cases}$

前一个表示不把任何物品放入背包，后一个表示背包容量为 0。显然两种情况下，最大的价值都只能为 0。

这样一来，我们就有了完整的目标函数的定义:

$F(i,\ c) = \\ \left\{ \begin{aligned} &0 &c = 0\ \text{ or } i = 0\\ &F(i-1,\ c) &c < w_i\\ &\max{\{F(i-1, c), F(i - 1,\ c - w_i) + v_i\}} &\text{other cases} \end{aligned} \right.$

代码实现

有了以上的分析，我们可以得出基本的算法框架。我们一个一个地考察物品，每次都尝试着把一个新的物品放入到背包中，看会发生什么，直到所有的 N 的物品全部考察完毕为止。

F[0, 0..C] = 0
for i = 1 to N
    for c = Ci, i = 1 to C
        if i 可以放入容量为 c 的背包
            F[i, c] = max {F[i − 1, c], F[i − 1, c − Wi] + Vi}
        else
            F[i, c] = F[i - 1, c]
        end
    end
end

具体实现如下:

const int items = 10;
const int capacity = 20;
int weight[items + 1];
int value[items + 1];
bool used[items + 1];
//dp[i][j]: 前 i 件物品放入容量为 j 的背包里产生的最大价值
int dp[items + 1][capacity + 1];

void Knapsack()
{
    //放入容量为 0 的背包里，价值为 0
    for (int i = 0; i <= items; ++i)
        dp[i][0] = 0;
    //没有东西放入，价值为 0
    for (int c = 0; c <= capacity; ++c)
        dp[0][c] = 0;
    //DP
    int v_i, w_i;
    for (int i = 1; i <= items; ++i)
    {
        for (int c = 1; c <= capacity; ++c)
        {
            //第 i 件物品的价值和重量 (1 <= i <= items)
            v_i = value[i];
            w_i = weight[i];
            //如果剩余的容量比 w_i 还小，那物品 i 肯定放不进来
            if (c < w_i)
            {
                dp[i][c] = dp[i - 1][c];
            }
            //否则，就有两种选择: 放入或者不放入
            else
            {
                //方案一: 不把物品 i 放入背包
                //则获得的价值和把前 i - 1 个物品放入容量为 c 的背包中相同
                int reward1 = dp[i - 1][c];
                //方案二: 把物品 i 放入背包
                int reward2 = dp[i - 1][c - w_i] + v_i;
                //取价值更大的一种方案
                dp[i][c] = max(reward1, reward2);
            }
        }
    }
}

int main()
{
    for (int i = 1; i <= items; ++i)
    {
        cout << "Item " << i << ": ";
        cin >> weight[i] >> value[i];
    }
    Knapsack();
    cout << dp[items][capacity] << endl;
    return 0;
}

查看使用了哪些物品

通过 dp 数组可以反向查看哪些物品放入了背包。思路很简单，从后往前遍历 dp，如果 dp[i][c] > dp[i - 1][c]，说明物品 i 肯定放入背包中了。

void UseWhich()
{
    //首先从 dp[items][capacity] 查起
    int c = capacity;
    for (int i = items; i >= 1; --i)
    {
        //看看是不是用了
        if (dp[i][c] > dp[i - 1][c])
        {
            used[i] = true;
            c = c - weight[i];
        }
        else
            used[i] = false;
    }
    int v = 0;
    c = capacity;
    for (int i = 1; i <= items; ++i)
    {
        if (used[i])
        {
            v += value[i];
            c -= weight[i];
            cout << "Item " << i << " used! ";
            cout << "Value: " << value[i];
            cout << ", Weight: " << weight[i];
            cout << ", TotalValue: " << v;
            cout << ", LeftCapacity: " << c << endl;
        }
    }
}

2. 优化空间复杂度

以上方法的时间和空间复杂度均为 $O(N\times C)$ ，其中时间复杂度应该已经不能再优化了，但空间复杂度却可以优化到 $O(C)$ 。

我们来仔细看看用到的状态转移式子:

F[i, c] = max {F[i − 1, c], F[i − 1, c − Wi] + Vi}
F[i, c] = F[i - 1, c]

把算法抽象一下，其实是这样的:

for i = 1 to N
    for c = c1 to cn
        F[i, c] = F[i - 1, xxx]

也就是说要填充 F[i, c] 的内容，需要用的两部分数据:

同一行的某个数据
上一行正对应的数据

稍加思考我们发现这个迭代式子完全可以改成这样:

for i = 1 to N
    for c = c1 to cn
        F[c] <- F[xxx]

为啥？因为前面的 i - 1 行数据压根就用不到啊！既然用不到，那干嘛不干脆扔了算了呢？

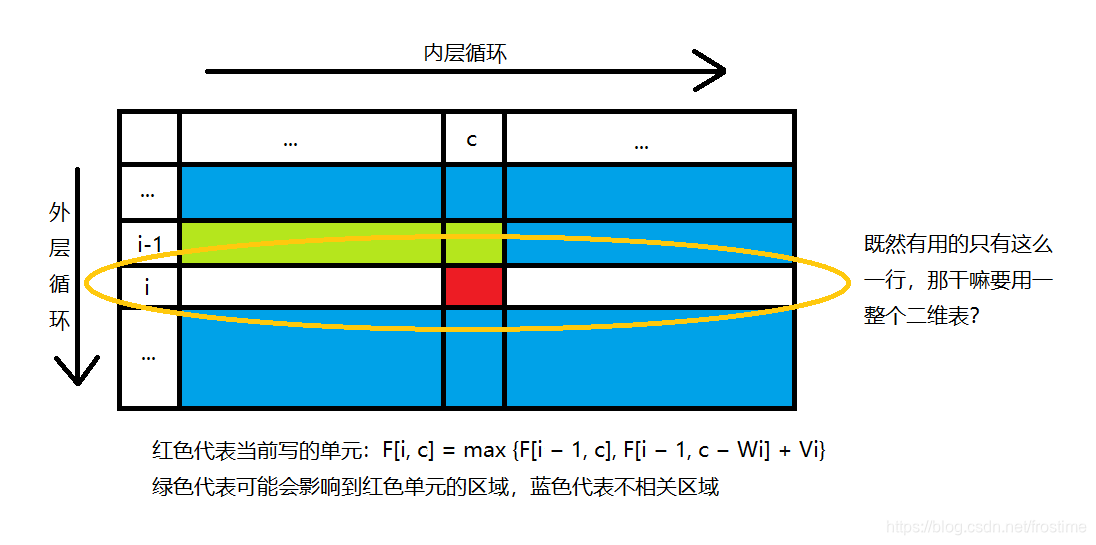
在这里插入图片描述

这样的思路，叫做“滚动数组”，这在动规中是一个很常用的缩减空间开销的法子。用了滚动数组后，原本的 dp[items][capacity] 就变成了 dp[capacity]。在整个外层循环期间，我们可以把 dp[capacity] 形象地想象成一个在 dp[items][capacity] 上不断往下滚动的窗口，透过窗口，我们看到的就是当前行的 dp[items][capacity] 的数据。由于只保留了当前的数据，以前的数据全部丢弃，所以大大减少了空间消耗。

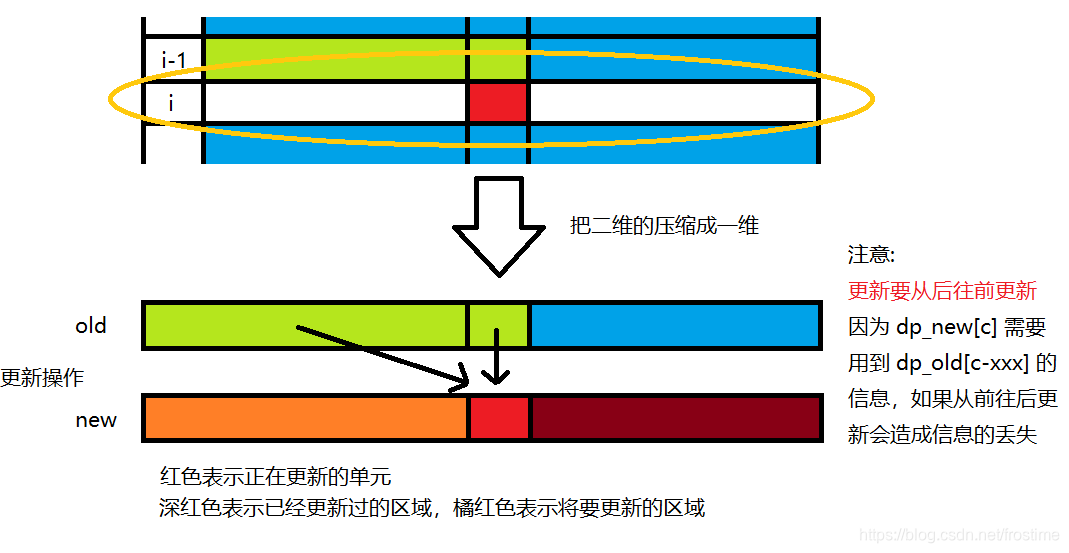
在这里插入图片描述

特别需要注意的是，实现的时候内层循环要从后往前来进行。

这是因为从 F[i, c] = max {F[i − 1, c], F[i − 1, c − Wi] + Vi} 可以看出，F[i, c] 要用到老数据中考前部分的数据，如果从前往后更新，就会造成信息的丢失。

int dp[MAX_CAPACITY + 1];
void Knapsack()
{
    //在空间为 0 的背包内放入
    dp[0] = 0;
    for (int i = 1; i <= items; ++i)
    {
        for (int c = capacity; c >= 1; --c)
        {
            //只有在能放入物品的时候才做一下更新
            if (c >= weight[i])
            {
                //不放入
                int reward1 = dp[c];
                //放入
                int reward2 = dp[c - weight[i]] + value[i];
                dp[c] = max(reward1, reward2);
            }
        }
    }
}

3. 初始化条件

我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。

有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。

如果是第一种问法，要求恰好装满背包，那么在初始化时除了 $F[0]$ 为 0 ，其
它 $F[1...C]$ 均设为 -∞ ，这样就可以保证最终得到的 $F[C]$ 是一种恰好装满背包的最优解。

如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该
将 $F[0...C]$ 全部设为 0。

可以这样理解：初始化的 $F$ 数组事实上就是在没有任何物品可以放入背包时的合法状态。

如果要求背包恰好装满，那么此时只有容量为 0 的背包可以在什么也不装且价值为 0 的情况下被“恰好装满”，其它容量的
背包均没有合法的解，属于未定义的状态，应该被赋值为 -∞ 了。

如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的
价值为 0，所以初始时状态的值也就全部为 0 了。

参考资料

《背包九讲》
《算法设计与分析》

01背包问题完全详解