非线性方程求解：弦截法和抛物线法

非线性方程求解：弦截法和抛物线法

牛顿迭代法虽然具有收敛速度快的优点，但每迭代一次都要计算函数导数，

而有些函数的导数计算十分麻烦。

弦截法和抛物线法便是为了避免上述不便而提出的方法.

一、弦截法：

$牛顿迭代公式：\\ x_{k+1}=x_k-\frac{f(x_k)}{f^{'}(x_k)}\\$

替换牛顿公式中的f’(x),便得到迭代公式：
$x_{k+1}=x_k-\frac{f(x_k)(x_k-x_{k-1})}{f(x_k)-f(x_{k-1})}\\ 这就是弦截迭代公式.$

算法流程：

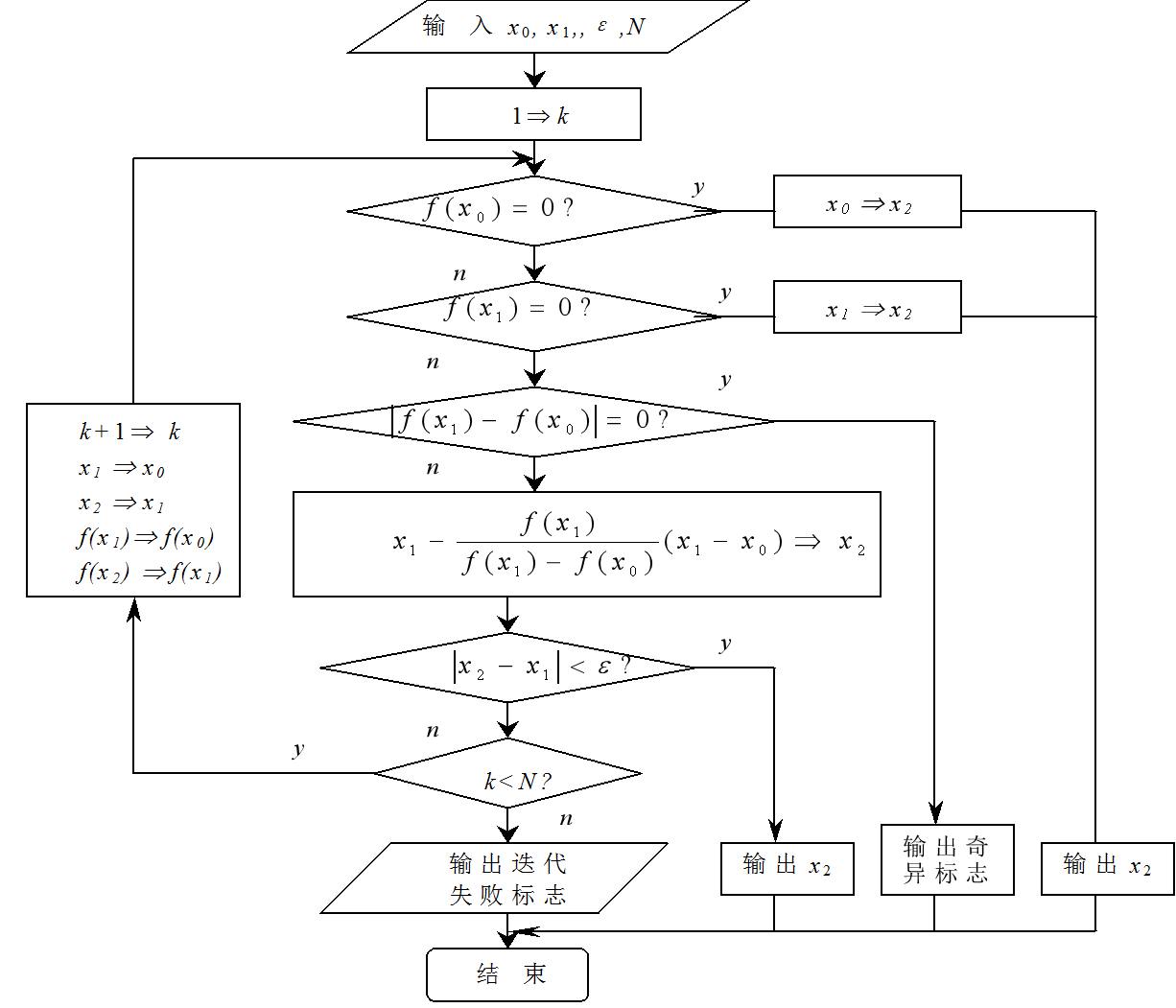
注意，弦截迭代发要用到前两步的结果：

$x_{k}和x_{k-1}.$

二、抛物线法

根据牛顿多项式插值公式：
$N_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+...+a_n(x-x_0)(x-x_1)\cdots(x-x_{n-1})$
取三次牛顿插值公式得：
$N_2(x)=f(x_k)+f[x_k,x_{k-1}](x-x_k)+f[x_k,x_{k-1},x_{k-2}](x-x_k)(x-x_{k-1})$
令上式等于0，得到：
$x_{k+1}=x_k-\frac{2f(x_k)}{\omega±\sqrt{\omega-4f(x_k)f[x_k,x_{k-1},x_{k-2}]}}\\ 式中：\\$

$\begin{cases} f[x_k,x_{k-1}]=\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}} \\ \\ f[x_k,x_{k-1},x_{k-2}](x_k-x_{k-1})= \frac{f[x_k,x_{k-1}]-f[x_{k-2},x_{k-2}]}{x_k-x_{k-2}}\\ \\ \omega=f[x_k,x_{k-1}]+f[x_k,x_{k-1},x_{k-2}](x_k-x_{k-1})\\ \end{cases}$

上式计算可以得到两个值，选择解得时候应该选择离xk更接近的解.

弦截法和抛物线法只是对迭代公式进行了更改，并不影响算法的流程，可以参考链接中的代码进行算法仿真.

链接非线性方程求解 ：二分迭代法和牛顿迭代法