当我们拟合了一个线性回归模型以后,我们需要检验归回模型预测的准确度,这时候我们可能需要计算预测值和实际值之间的残差,理论上残差应服从正太(高斯)分布,那么如何来检验数据是否服从正太分布呢?我们可以通过画QQ图的方式来直观的检验数据是否服从正太分布:

我之前写的一篇有关方房价预测的博客中简单说明了如何来画QQ图,今天我打算对概率计算中的一些概念做一下梳理,在厘清这些基本概念之后,我们将使用python对这些概念进行可视化,学会如何可视化数据我们以后从事数据分析,机器学习等方面的工作都会有很大的帮助。下面我们将从正太分布开始讲起。
正太分布介绍
正太分布是一种连续型的随机变量(随机变量可分为连续型和离散型两种),它具有如下三个性质:
- 单峰,对称,形状宛如一个钟,俗称钟型曲线
- 严格遵循一个法则:数据分布在均值的周围
- 许多变量都是近似正太随机变量,现实中不存在100%的正太随机变量。
正太分布随机变量有两个关键参数,μ和σ,他们分别表示均值(mean)和标准差(sd)。

不同的μ和σ表示正太分布曲线形状上的差异:

正太分布的经验法则:68-95-99.7%
对于正太分布有一个非常重要的经验法则“68-95-99.7%”,所谓68是指服从正太分布的数据集中有68%的数据分布在均值的±1个标准差的范围内,所谓95是指服从正太分布的数据集中有95%的数据分布在均值的±2个标准差的范围内,所谓99.7是指服从正太分布的数据集中有99.7%的数据分布在均值的±3个标准差的范围内,±3个标准差的范围之外的数据就是我们俗称的“异常值”,这里的68%,95%,99.7%指的是正太分布曲线下方的面积(它代表着概率),整个钟型曲线下方的面积从-∞至+∞范围内的面积总和为1,对于像正太分布这样的连续型随机变量,我们关心的只是曲线下方某个区间的面积,因为它代表着概率,而不会去关心曲线上某个点的纵坐标的值,曲线下方某个区间的面积越大,概率也越大,面积越小,概率越小,请记住正太分布我们只关心曲线下方的面积!:

讲了这么多,我们来个例子吧:假如一个医生收集了大量人体心率变化的数据,他对这些数据进行了统计并得到了3个统计量:数据中心率的平均值是mean=110次/分钟,心率的最小值是minimum=65次/分钟,心率的最大值是maximum=155次/分钟,请问数据的标准差应该是多少?(即知道数据的平均值、最小值、最大值求数据的标准差)
解答
首先通过常识我们可以判断出人的心率变化应该服从正太分布,其次题目中只给出了3个统计量(均值、最小值、最大值)的情况下,我们可以默认的认为最小值和最大值应该处于±3个的标准差的位置,好,知道他们分别位于±3个的标准差的位置,那么1个标准差的位置就可以被确定下来:
σ=(110-65)÷3=15 或者 σ=(155-110)÷3=15 即:
110 ± (3×15) = (65,155)

再来一题:SAT和ACT是两种美国高考的形式,学生Pam参加了SAT考试,成绩是1800分,学生Jim参加了ACT考试成绩是24分。并且我们知道了SAT和ACT成绩一些参数:
- SAT~N(mean=1500, sd=300) (这表示SAT成绩服从均值为1500和标准差为300的正太分布)
- ACT~N(mean=21, sd=5) (这表示ACT成绩服从均值为21和标准差为5的正太分布)
有一所大学想录取Pam和Jim中成绩较好的一位,那么如何确定谁的成绩更好呢?

解答
由于SAT和ACT的分制不同,因此我们无法直接比较两个人的成绩,在这种情况下,我们一般将两人的成绩转换成标准正太分布:

将两人的分数转换成标准正太分布后,Pam的成绩落在1的位置,而Jim的成绩落在了0.6的位置。我们可以这样理解:在标准正太分布的曲线下,Pam的成绩所覆盖的面积(-∞至1)要比Jim的成绩所覆盖的面积(-∞至0.6)要大,Pam的成绩高于84.1%的学生,而Jim的成绩只高于72.6%的学生,因此Pam的成绩要Jim的成绩更好:

使用Z分数来进行标准化
正如前面例子中所描述的,由于SAT和ACT考试的分制不一样,因此无法直接比较Pam和Jim的成绩,在这种情况下我们要对他们的成绩进行标准化处理,我们通过计算它们的Z分数,可以将它们转换成标准正太分布。这种对数据的标准化处理方式类似与机器学习中的归一化处理。
- 观察值的标准化(Z)分数是指高于或低于平均值的标准差的数量
- Z分数的均值为0
- 异常值在±2个标准差之外


百分比的计算
我们使用以下三种方法来计算百分比:
- 使用Python来计算百分比
- 使用图形法计算百分比
- 使用查表法来计算百分比

使用web分布图形法:https://gallery.shinyapps.io/dist_calc/

使用查表法:我们的概率统计书籍的附录中会有一张类似于这样的表,可以根据Z分数小数点后一位和后两位来查询它所对应的百分比:

查表时根据Z分数小数点的后一位和后两位来确定百分比


Pam成绩的百分比为0.8413,这意味着Pam的成绩高于84.13%的学生,但另外还有15.87%的学生成绩高于Pam。我们再来一题:

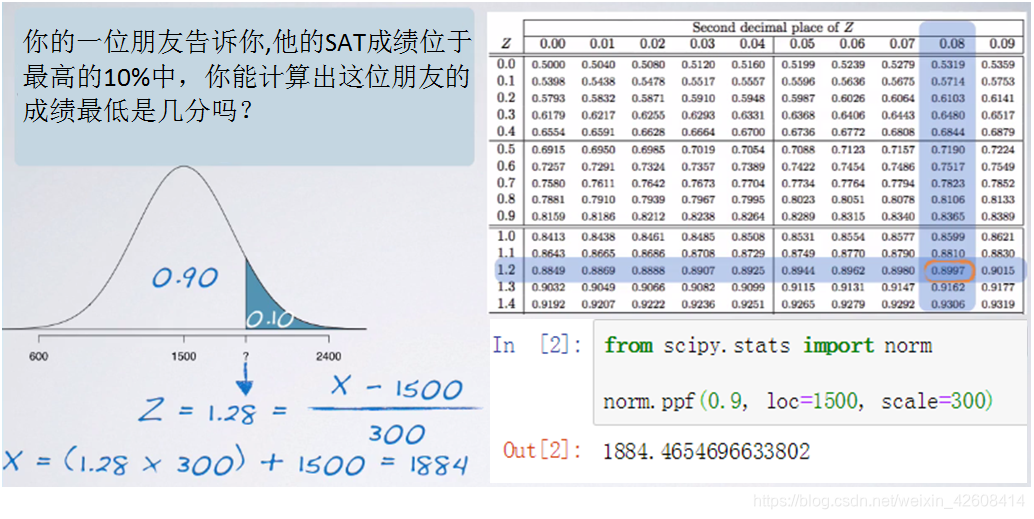
这位朋友的成绩位于最高的10%中,这也就意味着他的成绩将高于其余90%的人。接下来我们利用查表法来查找最接近90%的百分比为0.899。并由0.899所在的行首和列首此得到Z分数小数点后一位和后两位,最后我们得到Pam的Z分数为1.28:

有了Z分数,均值和标准差,Pam这位朋友的最低分应该不难求出,接下来我们将使用pyth和手工计算这两种方式来计算Pam朋友的最低分数:
正态分布的可视化
未完待续。。。
