原文链接

今天来讲一讲树状数组的用法，树状数组是包含在线段树里面的，树状数组能做的线段树一定能做，但是树状数组代码非常短，因此得以应用

lowbit（(这个地方有一点需要注意：lowbit(0)会陷入死循环 )）

先来准备学习树状数组之前需要的知识，树状数组是基于二进制的，给定一个数A，lowbit就是求A的二进制的的最后一个1的位置，准确的说是把A这个数最后一个1前面的数都删去，比如二进制A=00110，lowbit(A)=10，那么怎么实现lowbit的这个功能呢？其实就是lowbit(A)=A&(-A)，就是（一个数）与上（这个数按位取反之后加一的那个数），不难理解一个数按位取反之后再加一该进位的进位后只会留下最后一个1，只要知道这个函数咋写就行了

int lowbit(x){return x&(-x);}

基本原理

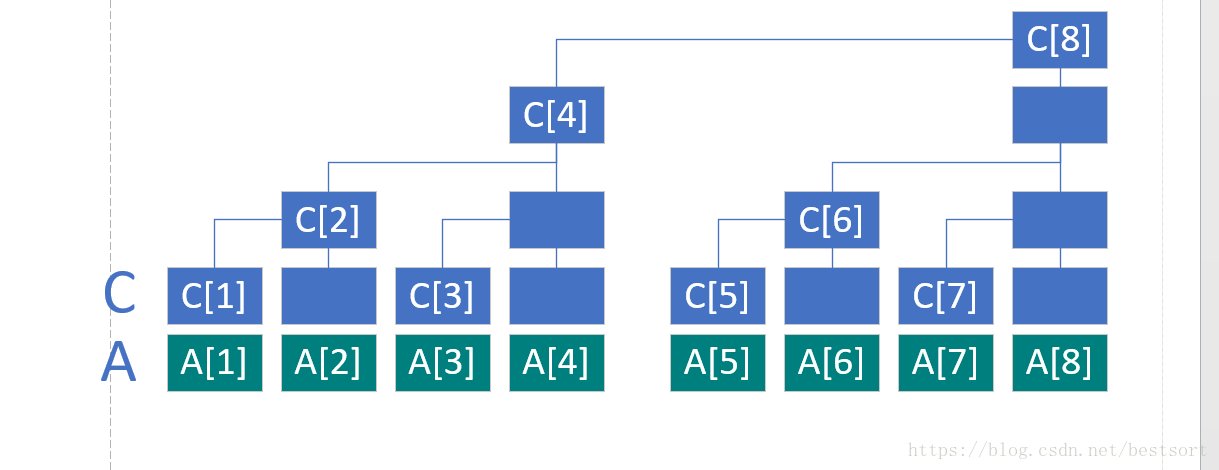
看这个图，树状数组是基于二分的思想，和二叉树相似，只不过二分的位置变了,最底下一层是原数组

C[i]代表子树的叶子结点的权值之和

如图可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

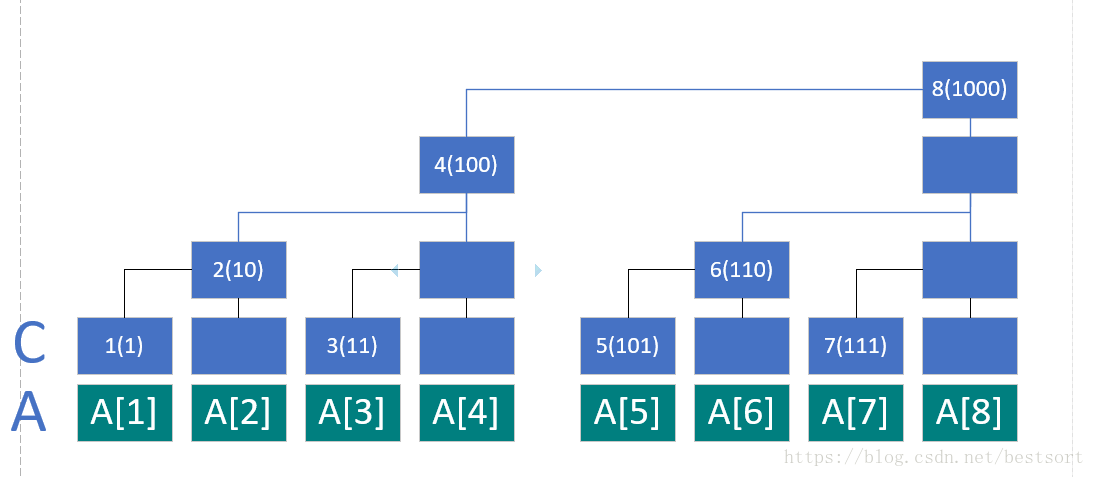
再将其转化为二进制看一下:

C[1] = C[0001] = A[1];

C[2] = C[0010] = A[1]+A[2];

C[3] = C[0011] = A[3];

C[4] = C[0100] = A[1]+A[2]+A[3]+A[4];

C[5] = C[0101] = A[5];

C[6] = C[0110] = A[5]+A[6];

C[7] = C[0111] = A[7];

C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

对照式子可以发现 C[i]=A[i-2^k+1]+A[i-2k+2]+…A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8(1000)时，k=3;

C[8] = A[8-2^3+1]+A[8-23+2]+…+A[8]

现在我们返回到lowbit中来

其实不难看出lowbit(i)便是上面的2^k

因为2^k后面一定有k个0

比如说2^5==>100000

正好是i最低位的1加上后缀0所得的值

这样就通过lowbit建立了层与层之间的关系，每次当底层的某个数改变了，通过lowbit可以找到这个数的上级，让上级改变同样的值，再通过lowbit找到上上级，改变同样的值，知道顶峰

可能上面的图有的地方有空缺，不好看，可以看这张图

单点更新

此时如果我们要更改A[1]

则有以下需要进行同步更新

1(001)： C[1]+=A[1]

lowbit(1)=001 1+lowbit(1)=2(010)： C[2]+=A[1]

lowbit(2)=010 2+lowbit(2)=4(100)： C[4]+=A[1]

lowbit(4)=100 4+lowbit(4)=8(1000)： C[8]+=A[1]

换成代码就是:

    void add(int x,int y,int n){
        for(int i=x;i<=n;i+=lowbit(i))    //x为更新的位置,y为更新后的数,n为数组容量
            c[i] += y;
    }

区间查询

改变某个数是从下级往上级报，而查询就是上级向下级走了，依旧是通过lowbit

举个例子 i=5

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

可以推出: sum(i = 5) ==> C[4]+C[5];

序号写为二进制: sum(101)=C[(100)]+C[(101)];

第一次101,减去最低位的1就是100;

其实也就是单点更新的逆操作

int getsum(int x){
    int ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += c[i];
    return ans;
}

lowbit会了,区间查询有了,单点更新也有了接下来该做题了

http://acm.hdu.edu.cn/showproblem.php?pid=1166

Code

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <string>
#include <vector>
#define For(a,b) for(int a=0;a<b;a++)
#define mem(a,b) memset(a,b,sizeof(a))
#define _mem(a,b) memset(a,0,(b+1)<<2)
#define lowbit(a) ((a)&-(a))
using namespace std;
typedef long long ll;
const int maxn =  5*1e4+5;
const int INF = 0x3f3f3f3f;
int c[maxn];
void update(int x,int y,int n){
    for(int i=x;i<=n;i+=lowbit(i))
        c[i] += y;
}
int getsum(int x){
    int ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += c[i];
    return ans;
}
int main()
{
    int t;
    int n;
    int x,y,z;
    string s;
    cin >> t ;
    for(int j=1;j<=t;j++){
        scanf("%d",&n);
        _mem(c,n);      //初始化数组中前n+1个数为0
        for(int i=1;i<=n;i++){
            scanf("%d",&z);
            update(i,z,n);
        }
        cout <<"Case "<<j<<":"<<endl;
        while(1){
            cin >> s;
            if(s[0] == 'E')
                break;
            scanf("%d%d",&x,&y);
            if(s[0] == 'Q')
                cout << getsum(y)-getsum(x-1)<<endl;
            else if(s[0] == 'A')
                update(x,y,n);
            else
                update(x,-y,n);
        }
    }
    return 0;
}

区间操作单点查询

上面是单点操作区间查询，也可以区间操作单点查询。

结合题目：
https://www.luogu.com.cn/problem/P3368

这道题是对一段区间进行某种操作，明显要用差分，可怎么再树状数组上用呢？我们知道差分数组的前缀和就是原数组进行修改过后的值，例子：设数组a[]={1,6,8,5,10}，那么差分数组b[]={1,5,2,-3,5}，我们知道树状数组就是求前n项的和，索性我们就让树状数组存储差分数组的值，你也可以理解为树状数组代替了前缀和

Code

#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(0)
using namespace std;
const int maxn=5e5+100;
typedef long long ll;
ll a[maxn],n;
int lowbit(int n){
	return n&(-n);
}
void add(int x,int y){
	for(int i=x;i<=n;i+=lowbit(i)){
		a[i]+=y;
	}
}
ll query(int n){
	ll ans=0;
	for(int i=n;i>0;i-=lowbit(i)){
		ans+=a[i];
	}
	return ans;
}
int main()
{
	int m; ios;
	cin>>n>>m;
	int last=0;
	for(int i=1;i<=n;i++){
		int t; cin>>t;
		add(i,t-last); //差分数组
		last=t;
	}
	while(m--){
		int x; cin>>x;
		if(x==1){
			int l,r,k;
			cin>>l>>r>>k;
			add(l,k);add(r+1,-k);
		}
		else{
			int t; cin>>t;
			cout<<query(t)<<endl; 
		}
	}
	return 0;
}

区间操作区间查询

参考原文

我们已经学会了树状数组的基本操作:单点修改区间查询,或区间修改单点查询(不会的话先去自学吧…这篇文章不适合你…).思考,区间修改单点求值是怎么做到的?只需要维护一个新数组c[i]=a[i]-a[i-1],也就是c[]是a[]的差分数组,修改区间[l,r]+v只需

add(l,v);add(r+1,v)

即可.求某个值的时候,只需要把差分数组的前缀和求出来,就是要求的了.
领悟了这个操作以后我们发现,化区间为单点的思想精髓就在于差分二字.利用差分思想,区间修改解决了,接下来就是区间求和公式的推导过程:

sum(1,n)

=a[1]+a[2]+a[3]+…+a[n-1]+a[n]

=c[1]+(c[1]+c[2])+…+(c[1]+c[2]+…+c[n])

=n(c[1]+c[2]+…+c[n])-(0c[1]+1c[2]+2c[3]+…+(n-1)c[n]).

发现什么了?

我们开第二个树状数组c2,令c2[i]=c[i] (i-1),那么…

区间修改[l,r]+=v:

add(c[l],v),add(c[r+1],-v);

add(c2[l],(l-1)v),add(c2[r+1],-rv);

求前缀和sum(1,n):

sum(1,n)=n*query_c(n)-query_c2(n).

求区间和sum(l,r):

sum(l,r)=sum( r )-sum(l-1).

至此,树状数组已经轻松实现了区间修改区间求和!

题目链接

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 102333
using namespace std;
typedef long long ll;
int n,m;
ll a[N],c1[N],c2[N];
inline int lowbit(int x){return x&(-x);}
void add(ll *r,int pos, ll v)   //区间修改 
{
    for(;pos<=n;pos+=lowbit(pos))r[pos]+=v;
}
ll getsum(ll *r,int pos)	//算前缀和 
{
    ll re=0;
    for(;pos>0;pos-=lowbit(pos)) re+=r[pos];
    return re;
}
ll sigma(int r)		//算修改后的前缀和 
{
    ll sum1=r*getsum(c1,r),sum2=getsum(c2,r);
    return sum1-sum2;
}
ll query(int x,int y)	//得出结果 
{
    return sigma(y)-sigma(x-1);
}
int flag,x,y;ll k;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
        add(c1,i,a[i]-a[i-1]);
        add(c2,i,(i-1)*(a[i]-a[i-1]));
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&flag);
        if(flag==1)
        {
            scanf("%d%d%lld",&x,&y,&k);
            add(c1,x,k);add(c1,y+1,-k);
            add(c2,x,(x-1)*k);add(c2,y+1,y*(-k));
        }
        else
        {
            scanf("%d%d",&x,&y);
            printf("%lld\n",query(x,y));
        }
    }
    return 0;
}

树状数组及其扩展

lowbit（(这个地方有一点需要注意：lowbit(0)会陷入死循环 )）

基本原理

单点更新

区间查询

Code

区间操作单点查询

Code

区间操作区间查询

Code

猜你喜欢