差分法是我们所用的一个强力的武器！

~~有这把武器你就可以统治世界。。。~~

一个大佬曾经讲过，一但碰到区间修改的题，就要优先考虑差分。

普通差分法

我们有时做题，会发现这么一种题。

给你长度为n的序列，m次操作，有两种：1. 让[l,r]区间加上k。2. 查询一个点的值。

典型的区间修改，单点查询。
单点查询简单。
但是区间修改怎么做？
~~暴力卡常。。。~~
~~线段树。。。~~
比较正经的做法是差分，差分是什么？

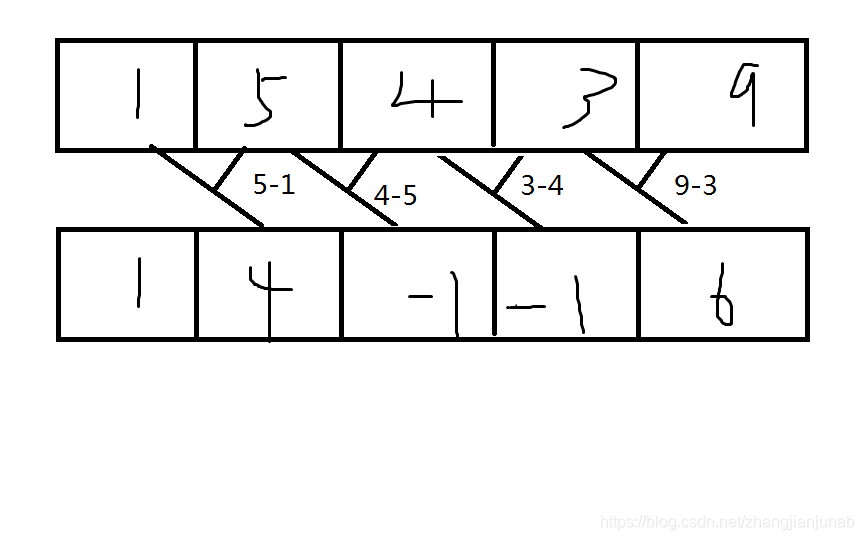
在这里插入图片描述

对于一个序列a，定义另一个序列b， $b[i]=a[i]-a[i-1]$ ，则叫b数组为a数组的差分数组，这样有什么优势呢？

首先，如果要求a[i]，我们会发现就是 $b[i]+a[i-1]$ ，不断拆开， $a[i]=b[i]+b[i-1]+b[i-2]+b[i-3]+....+b[1]$ ，是不是很棒棒，就是前缀和！

~~但是单点查询O(n)呀~~

先讲这样怎么修改，假设是 $[l,r]$ 区间加上k，那么我们就让 $b[l]$ 加上 $k$ ，让 $b[r+1]$ 减去 $k$ 就行了。这样，在 $[l,r]$ 区间内，每个数都会加上 $b[l]$ 多出的 $k$ ，但是在 $r$ 之后，我们也会因为 $b[r+1]$ 减去了 $k$ 从而和 $b[l]$ 的 $k$ 抵消。

这样，区间修改就完成了！

但是单点查询又复杂了，它可以表达成前缀和，前缀和…树状数组维护就可以了！
是不是很不错！

这里给大家一点扩展！

至于树状数组区间查询，区间修改，我粘上一个大佬的话，我认为很不错！

我们还是需要引入delta数组，这里的delta[i]表示区间a[i…j]都需要加上的值的和。那么当我们需要将区间[l,r]上的每个数都加上x时，我们还是可以直接在树状数组上将delta[l]加上x，delta[r+1]减去x。

那么问题来了，如何查询区间[l,r]的和？

我们设a[1…i]的和为sum[i]，根据delta数组的定义，则：

$sum[i]=\sum_{j=1}^ia[j]+\sum_{j=1}^idelta[j]*(i-j+1)$
$sum[i]=\sum_{j=1}^ia[j]+(i+1)*\sum_{j=1}^idelta[j]-\sum_{j=1}^idelta[j]*j$

这样我们就不难看sum[i]是由哪三个部分组成的了。我们需要用一个asum数组维护a数组的前缀和，delta1与delta2两个树状数组，delta1维护delta数组的和，delta2维护delta[i]*i的和，代码如下：

void add(int *arr int pos,int x){
    while(pos<=n) arr[pos]+=x,pos+=lowbit(pos);
}
void modify(int l,int r,int x){
    add(d1,l,x),add(d1,r+1,-x),add(d2,l,x*l),add(d2,r+1,-x*(r+1));
}
int getsum(int *arr,int pos){
    int sum=0;
    while(pos) sum+=arr[pos],pos-=lowbit(pos);
    return sum;
}
int query(int l,int r){
    return asum[r]+r*getsum(d1,r)-getsum(d2,r)-(asum[l-1]+l*getsum(d1,l-1)-getsum(d2,l-1));
}

摘自

咳咳，回归正题，总结一下
普通差分就是这个数减去前一个数所得到的一个数组，他不是个算法，只是种技巧，比如在树状数组中的妙用，让树状数组具有区间查询，单点修改的功能。

差分套差分（二阶差分）

没错你没有听错，差分都可以套了！

好像又叫二阶差分。

怎么套？将差分数组再差分一遍，求到了差分套差分的数组，定位c数组。

那么，推一推，发现 $a[i]=c[i]*1+c[i-1]*2+...+c[1]*(i-1)$

嗯，这个有什么用呢？

如果有一个毒瘤出题人，出了一道题（就是我被坑了，就写出来了）：

给你一个长度为n的序列a，有m次操作，每次操作让区间[l,r]分别加上t,t*2,t*3,...,t*(r-l+1)
最后输出a序列的每个数的值

把1操作中加上的数差分，就为 $t,t,t,t,t,...,t$ （注意：以后求高阶差分的修改公式，将加上的数组也进行差分来推是最好的！），那么，就等于给a的差分数组b区间加上t，那么就将b再差分出另一个差分数组c来更改，最后O(n)输出一下答案就好了。

当然，相比差分，差分套差分会有更多应用，欢迎大家探究！

高阶差分

这个就很毒瘤了，一般没有人出这种题。~~讲一下就是希望以后有什么人出这种毒瘤题~~

我们通过列三阶差分，设数组为d，则有 $a[i]=1*d[i]+3*d[i-1]+6*d[i-2]+10*d[i-3]+...（猴子的脑子烧焦了...）$
我们观察到 $3-1=2,6-3=3,10-6=4...$ 这不是二阶等差数列吗？

继续观察：

我们发现n阶差分数组单点查询就等于n-1阶差分数组的前缀和，也就是说，而我们发现从三阶开始， $d[i]=c[i]+c[i-1]+c[i-2]..+c[1]$ ，而 $c[i]=1*a[i]+2*a[i-1]+...+(i-1)*a[1]$ ，也就是等差数列，我们将 $c[i]、c[i-1]、c[i-2]...$ 逐渐拆开，会发现 $a[j](j<=i)$ 的系数会在 $c[i],c[i-1],...,c[j]$ 中加上 $1,2,3,...,(i-j+1)$ 而a[j+1]的系数减去a[j]的系数就是(j-i+1)，所以从i到1的系数不就是个二阶等差数列吗？

继续推下去，我们发现n阶差分从i到1的系数就是 $(n-1)$ 阶的等差数列。

PS：n阶等差数列：相邻两两数之间的差是 $(n-1)$ 等差数列的数列，0阶数列就是一个常数序列。
如：1 4 9 16 25 36，减完后为3 5 7 9 11，则1 4 9 16 25 36是二阶等差数列

注意，我们把 $(n-1)$ 阶的等差数列之间每个数的差当成一个数列取出来，这个数列就是 $(n-2)$ 阶的等差数列，比如： $1,3,6,10$ 将两两差取出，就是 $1,2,3,4$ 一个一阶等差数列。（1是由 $1-0$ 得出来的）那么，不断的进行操作，我们最后会将这个 $(n-1)$ 阶的等差数列得到一个首项为1，等差为1的等差数列，这是比较重要的。

建议跳过的自己乱搞的东西。。。

至于等差数列求第i项公式，表示并不会，网上也没有找到，但是预处理一遍不好吗？~~就是你不会公示吧！~~

如果有哪位大佬会的话，麻烦发一下评论，我能修改一下我的博客，如果只会二阶的求前i项和的公式，也请发出来，谢谢！

先讲讲我捞比了两个小时的成果。

先发出来二阶等差数列求第i项的公式：
$b[i]=b[1]+a[1]*(i-1)+t*((i-1)*(i-2)/2)，b[1]为二阶等差数列首项，a[1]与t是原数列的一阶等差数列的首项与公差$
三阶的公式：
$c[1]+b[1]*(i-1)+a[1]*(1+2+...+(i-2))+t*(1+3+6+...+(i-2)*(i-3)/2) ，变量意义与之前的意思差不多$
我们发现，系数从左到右，第一个乘1，第二个是0阶等差数列前i-1项和 $(1,1,1,1,1,1...)$ ，第二个是1阶等差数列前i-2项和 $(1,2,3,4,...)$ ，第三个是2阶等差数列前i-3项和 $(1,3,6,10...)$ ，所以我们可以大胆假设对于n阶等差数列求第i项值 $(i>=n)$ 则为：

$a[n][i]=a[n][1]*1+a[n-1][1]*(i-1)+a[n-2][1]*(1+2+3+...)+a[n-3][1]*(1+3+6+10...)+...+t*(n-1阶等差数列前i-n项和)$

注意：这里系数所求的 $j(j<n)$ 阶等差数列的和中，由 $j$ 阶等差数列推导出的0阶等差数列是 $(1,1,1,1,1...)$ ，而且推导出的 $k(k<=j)$ 阶的等差数列中首项都是1。

以上就是我瞎搞的成果了。。。
大佬：语言不通畅，还垃圾。
蒟蒻：这根本不是人看的。
我：我也看不懂我写了什么。。。
所有人：没图，差评。

树上等差数列

基本概念：

树上两点之间只有一条最短路径
树上两点只有一个最近公共祖先

1. 点差分

点差分求什么？

给你一棵树，并给你一些在树上的路径，让你求每个点在树上被经过的次数。

如~~整篇博客没一张图。。。~~：
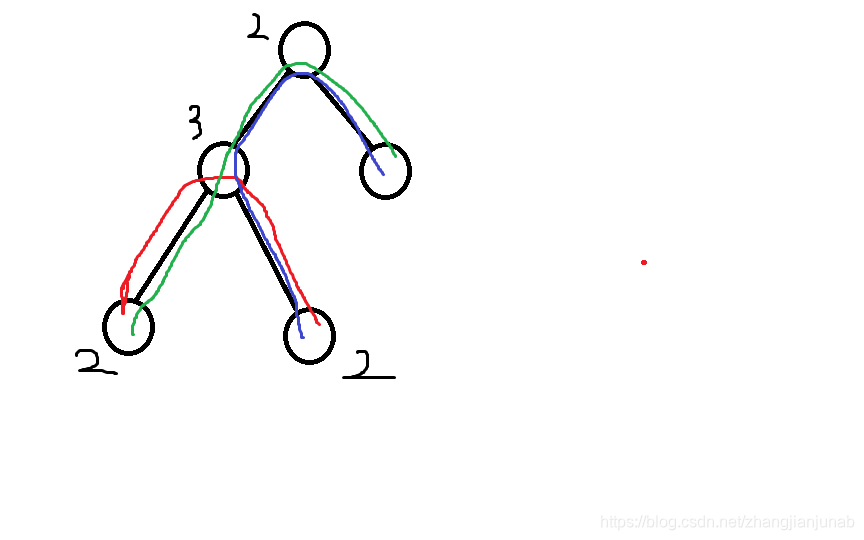
在这里插入图片描述
图中红色绿色蓝色代表三条路径，点旁边的标记代表他被经过的次数。

如何求？
暴力！
在这里插入图片描述

。。。
DFS暴力的话，肯定过不了呀！~~如果你送毒瘤出题人足够刀片说不定可以。。。~~

这时候，就有人跳出来发明了个算法，叫树上差分：
设路径的开头与结尾为 $st$ 与 $ed$ ，设 $k=lca(st,ed)$ ， $father_{k}$ 为 $k$ 的 $father$
那么我们把 $f[st]++,f[ed]++,f[k]--,f[father_{k}]--$ ，有什么用？
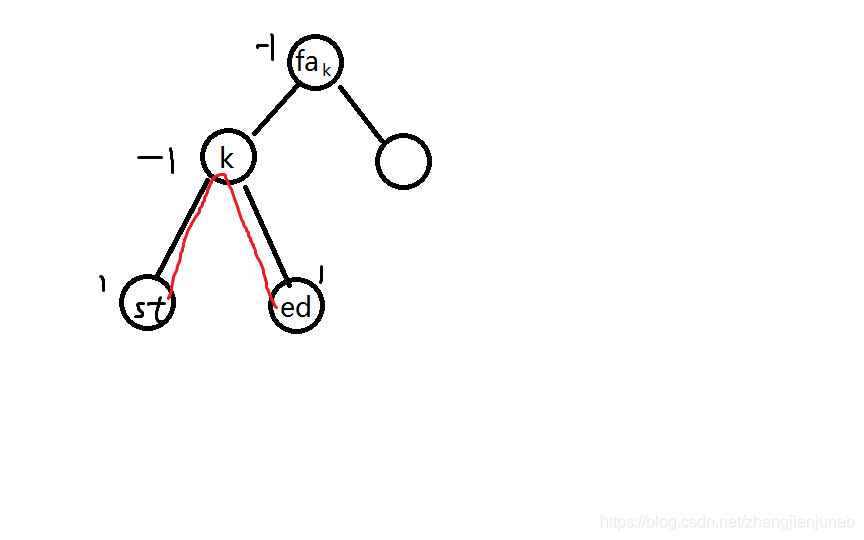
在这里插入图片描述

我们跑用DFS遍历一遍一棵树，设 $tot_{i}$ 为 $i$ 的子树的所有节点的 $f$ 和，如图：在 $st->ed$ 这条路径中，除了 $ed$ 外， $tot$ 值都是 $1$ ，又因为 $k$ 点的 $f$ 值为 $-1$ ，所以将一个1消掉了，所以 $k$ 的tot值也为1.

某银：那 $k$ 的父亲呢？

因为我们让 $father_{k}$ 的 $f值也减了1$ ，所以他和 $k$ 的1抵消了，所以并没有影响。

所以我们只需要 $O(1)$ 将所有路径处理完， $O(n)$ 遍历处理答案就好了！

2. 边差分

跟点差分差不多。

给你一棵树，并给你一些在树上的路径，让你求每条边在树上被经过的次数。

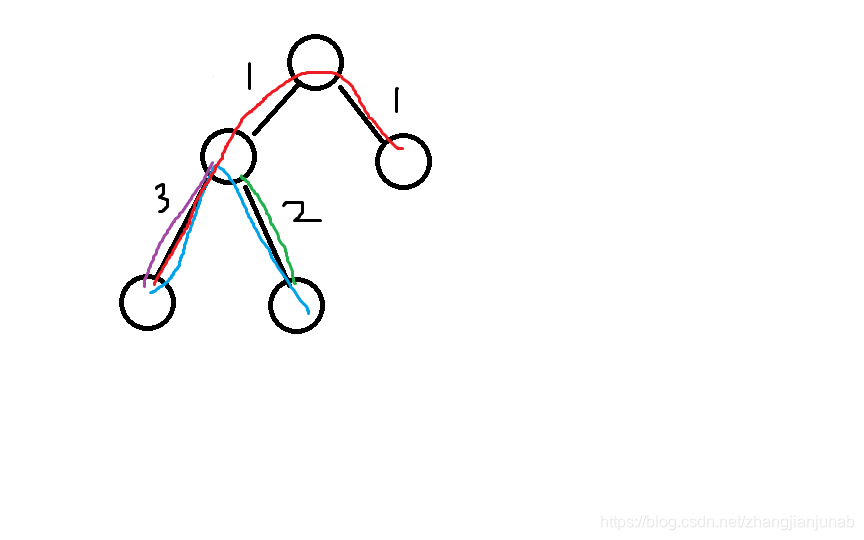
在这里插入图片描述

首先，我们应当考虑把边压到点里面，那么我们就让每个点到父亲的那条边压到这个点身上，然后求每个点被经过的次数就行了，点差分一下，有什么难？

恭喜你WA了。
在这里插入图片描述

难道你就没有发现只算一条路径的话， $k$ 到父亲这条边没有被经过，但是在点差分过程中 $tot_{k}=1$ 吗？所以，我们应当改一下修改 $f$ 值的过程。

$f[st]++,f[ed]++,f[k]-=2$

那么在 $k$ 点的时候，就把 $st、ed$ 的影响消掉了，是不是很舒服？

最后DFS一遍，别忘了每个点代表的是他到父亲的边！

那么不就解决了？

至此，基础的差分结束了。

终于写完了，ヾ(≧▽≦*)o，<(￣ˇ￣)/，～(￣▽￣～)(～￣▽￣)～,(:逃

欢迎大家D我，让我能更好的完善博客！

神奇的差分法（内附树状数组的一点扩展）

目录