机器学习模型之决策树

1、分类决策树模型

决策树模型是一种基于规则的算法，其是一个二叉树结构，其中叶子节点为分类的类别，中间的节点为对不同的特征的选择。其既可以做分类，也可以做回归，决策树学习算法包括特征选择，决策树的构建，剪枝。

1.1、特征选择

特征选择在进行决策树分裂的过程中进行的算法，其主要思想是希望在选择某个特征作为分裂特征之后，整个系统的熵变小。常用的特征选择算法有信息增益和信息增益比

• 信息增益
  首先，要想了解信息增益的原理，我们就需要理解两个概念，熵和条件熵，熵是什么呢？熵表示系统的混乱程度，或者叫不确定程度。
  
  设X为取有限个值的随机变量

\[ P(X = x_{i}) = p_{i} \tag{1} \]

则熵表示为

\[ H(X) = - \sum\limits_{i=1}^{n} p_{i} log p_{i} \tag{2} \]

我们可以看到，如果每个\(p_{i}\)都比较均匀的话，那么熵值就会很大，意味着整个系统就会很不确定。接下来我们引入条件熵，条件熵表示在某个随机变量下，另一个随机变量的混乱程度。公式如下

\[ H(Y|X) = \sum\limits_{i=1}^{n} p_{i}H(Y|X=x_{i}) \tag{3} \]

有了上述知识，我们就可以引出信息增益，其公式如下

\[ g(D,A) = H(D) - H(D|A) \tag{4} \]

可以理解为，数据集D的熵为\(H(D)\)，在\(A\)条件下的熵为\(H(D|A)\)，那就是说，当我们指定\(A\)之后，整体下降的熵即为信息增益，也可以理解为\(A\)帮助系统减少的混乱程度。一般情况下，我们也将信息增益当做\(D\)和\(A\)的互信息。

在决策树中，我们如何来理解信息增益呢？最开始的熵\(H(D)\)表示系统最开始的混乱程度，其公式为

\[ H(D) = - \sum\limits_{k=1}^{K} \frac {|C_{k}|}{|D|} * \log_2 \frac {|C_{k}|}{|D|} \tag{5} \]

其中\(K\)表示类别标签的数量，\(|C_{k}|\)表示在类别标签为\(k\)下的样本数量，\(|D|\)表示数据集样本总数量，这句话理解为类别标签越平均，则原始数据整体混乱。

接着，我们再看下\(H(D|A)\)的公式

\[ H(D|A) = \sum\limits_{i=1}{n}\frac {|D_{i}|}{|D|} H（D_{i}） \tag{6} \]

其中

\[ H（D_{i}）= - \sum\limits_{k=1}^{K} \frac {|D_{ik}|}{|D|} * \log_2 \frac {|D_{Ik}|}{|D|} \tag{7} \]

上面这两个式子怎么理解呢？首先，由于是在条件\(A\)下，所以我们要先算出每个特征占据整个数据集的百分比用\({|D_{i}|}{|D|}\)，接下来，我们就要计算在第\(i\)个特征下，这个特征的混乱程度，即\(H（D_{i}）\)，我们发现这个式子和\(H(D)\)基本类似，其原理也是一样，得到这个特征下的系统混乱程度，接下来，我们将所有特征所在的系统的混乱程度进行加和，最后，用信息增益公式(4)得到结果。

• 信息增益比

以信息增益来作为划分数据集的特征，存在数据偏向特征取值较多的特征，为了避免这一现象，提出了信息增益比

\[ g_{R}（D,A） = \frac {g(D,A)}{H_{A}（D）} \tag{8} \]

其中

\[ H_{A}（D） = - \sum\limits_{i=1}{n} \frac {|D_{i}|}{|D|} \log_2 \frac {|D_{i}|}{|D|} \tag{9} \]

1.2 决策树构建

ID3算法：利用信息增益作为选择特征的算法，从根节点开始依次构建决策树，直到没有可以选择的特征或者信息增益非常小，则不进行构建。

C4.5算法：利用信息增益比作为特征选择的算法。其他基本和ID3算法一样。

1.3 决策树剪枝

我们首先来定义决策树的损失函数

\[ C_{\alpha}(T) = \sum\limits_{t=1}{|T|} N_{t}H_{t}(T) + \alpha |T| \tag{10} \]

公式(10)中，\(|T|\)表示叶子节点的个数，\(H_{t}(T)\)表示叶子节点\(t\)经验熵，\(N_{t}\)表示该叶节点的样本个数。其中经验熵为

\[ H_{t} = - \sum\limits_{k} \frac {N_{tk}}{N_{t}} \log \frac {N_{tk}}{N_{t}} \]

剪枝过程分为预剪枝和后剪枝，预剪枝是在构建树的同时，计算分裂节点前和后的损失函数，如果分裂后损失函数增大，则进行剪枝。后剪枝是在树构建完成后，计算如果减去某一个叶子后，其损失函数若是减小，则进行剪枝。

2、分类回归树CART

2.1、回归树CART

回归树的基本算法就是对于每一类属性，我们将其进行切分，分为两个集合，这两个集合将这个属性分割开，接着我们计算在各自属性上的均方误差，最终选择均方误差最小的属性j以及其切分点s，将数据集分为两个部分，在树形结构中，也就是对节点进行分割，所以由此看来，最终我们得到的回归树是一个二叉树，接下来，我们对每一个部分同时进行上述方法，终止条件可以计算树的损失函数，损失函数请见(1.3)。

接下来介绍回归树生成算法

input:数据集D

output:回归树

• 选择最优切变量j和切分点s，利用公式

• 利用变量j和切分点s可以将数据集切分成两个部分，对两个部分，我们计算各自在不同变量j下的平均值。

2.2、分类树CART

2.2.1、基尼系数

基尼系数也表示了系统的不确定程度，和熵类似，基尼系数越小，表明系统越确定，其公式如下所示

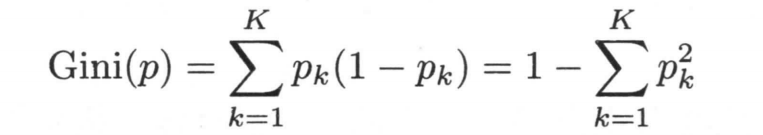
如果根据某个特征A，将整个数据集分成了两个部分S1，S2，则此时的基尼系数为

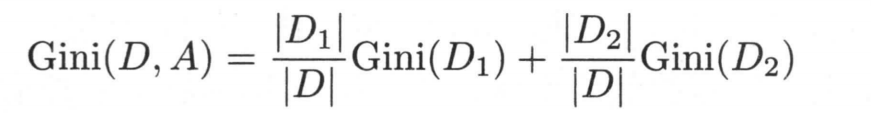
这里\(|D1|\)表示S1的样本数量，\(|D2|\)表示S2的样本数量。

2.2.2、分类树生成

input:数据集D

output:分类的CART树

• step1
  我们选取不同的特征值来把数据集分类两个部分，接着计算在这个特征下的总体基尼系数，接着我们选择使这个基尼系数最小的特征当做分割的特征。
• step2
  依次对分割后的两个子集进行分割
  

所以我们看到，最终CART生成的均为二叉树。