《无梯度优化（Derivative-Free Optimization）》

https://blog.csdn.net/fangqingan_java/article/details/48946903 数值优化（Numerical Optimization）学习系列-无梯度优化（Derivative-Free Optimization） ————————————————
在实际应用中，有些目标函数的梯度不容易计算，即使使用有限差分等近似算法，也会因为噪声的存在导致结果不精确。无梯度优化算法（DFO-Derivative-Free Optimization）可以在不计算梯度的情况下进行问题的最优化，主要有两类思路，一是根据目标函数的样本进行拟合，对拟合函数进行最优化；二是用一些启发式算法。 1. 有限差分和误差 2. 基于模型近似的方法 3. 坐标和模式搜索方法 4. 其他DFO方法 ———————————————— 基于模型的方法 主要思路是，在第k步迭代时，基于该点进行模型近似，通过采样推导出模型中的参数，基于该模型进行最优化计算。 扫描二维码关注公众号，回复： 11206260 查看本文章 ———————————————— 坐标和模式搜索方法 不同于梯度相关的算法，基于模式搜索方法的搜索方向都是事先确定好的，该方法需要从方向集合中选择一个下降方向作为搜索方向并且更新该方向集合，之后利用线搜索决定步长，逐步迭代得到最优解。 坐标下降是模式搜索方法中的一个特例。 坐标搜索方法（Coordinate SearchMethod） 该方法也称之为坐标下降法或者变量交替方法，主要思路是依次沿着坐标轴方向进行线搜索。 ———————————————— 模式搜索方法 每次搜索方向都是从一个“结构集”中选取，找到某个下降点，进行线搜索，否则修改步长，重复该过程。 该方法会受到噪声点、函数值不精确、不平滑的影响。
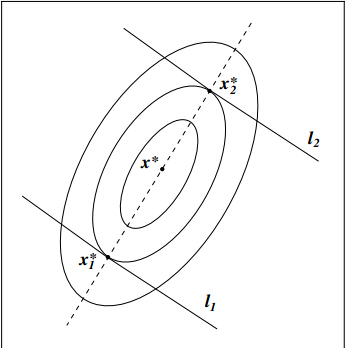
其他DFO算法： 共轭方向算法 类似于共轭梯度方法，该方法的目标是最优化 f(x)=12xTAx−bTxf(x)=12xTAx−bTx ，不同点在于共轭方向的计算仅仅依靠函数值得到，不依赖梯度的计算。 Parallel subspace property 通过该方法可以找到一系列共轭方向，并且沿着该方向可以得到最优解，以二维情况为例 如上图如果直线l1和l2平行，并且x1*和x2*是目标函数沿着该直线的最优解，则x1*-x2*共轭于直线的法向量。 因此只要沿着某两个平行子空间寻找最优解，则最优解的差就共轭于该平面的法向量。 Nelder-Mead 方法 也叫做Nelder-Mead simplex reflection方法。 保存n+1个点，并且这些点构成一个单纯性，在每次循环中搜索使得函数值最低的点，去掉后，用其他更好的点替代。 Implicit Filtering方法 对比于带有噪声的有限微分方法，适用于noise level随着迭代减小的情形。 总结 通过该小结的学习，可以了解到 1. 对于梯度不可求的复杂函数，可以通过DFO的方式进行优化 2. 通过随机试验估计函数值的最优化问题，可以考虑带噪声的有限差分。 3. 了解基于模型的方法，但是复杂度可能会比较大 4. 了解坐标下降法和模式搜索算法 5. 了解基于共轭方向等其他方法。 ————————————————
Nelder–Mead algorithm ( NM算法 ）其实是一种非常简单易懂的适用于在线最优化的算法。。。总的来说这个算法有些无脑。。。 收敛速度慢，效果一般般，因为适用范围较广（或者说unconstrained optimization，无固定模型也可以） 核心就是：向着最优的解收敛，不断抛弃更新现有的解 简介： 　　n维空间中，由n+1个顶点，可以组成“最简单”的图形，叫单纯形。 　　NM算法就是先构造一个出师的，包含给定点的单纯形。 　　然后使用可能的三种手段（反射，扩展，压缩）去替换函数值最差的顶点。 　　在以上三种手段失效的时候，使用收缩。 　　直到该单纯形的半径足够的小。 　　（半径的定义可以有很多，比如两两点的距离，两两点构成的向量中最大的维度的值， 只要当“半径”趋近与0的时候，该单纯形趋于一个点即可） 以下来自wiki： 理解： Reflection：以最优点为中心，做最差点的反射点，来达到抛弃最差点的目的。 Expansion：扩大最优点的优势，尝试是否能够得到更优的解。 Contraction：收缩搜索范围。 Shrink：整体向着最优解收缩。
7.1 Description and Analysis of Implicit Filtering 7.1 Description and Analysis of Implicit Filtering The implicit filtering algorithm was originally formulated in [270], [251], and [271], as a difference-gradient implementation of the gradient projection algorithm [18] in which the difference increment is reduced in size as the iteration progresses. A different formulation for unconstrained problems with certain convexity properties was introduced at about the same time in [279]. From the point of view of this book, the simplex gradient is used in a direct way. The algorithmic description and analysis in this chapter uses the results from §6.2 directly. We will focus on unconstrained problems and derive the convergence results that implicit filtering shares with the search algorithms in Chapter 8. Implicit filtering, by using an approximate gradient directly, offers the possibility of improved performance with quasi-Newton methods and can be easily applied to bound constrained problems. We explore these two possibilities in §§7.2 and 7.4. In its simplest unconstrained form, implicit filtering is the steepest descent algorithm with difference gradients, where the difference increment varies as the iteration progresses. Because the gradient is only an approximation, the computed steepest descent direction may fail to be a descent direction and the line search may fail. In this event, the difference increment is reduced.
最优化问题概述  *介绍最优化问题分类以及求解思路 线搜索方法  *基于线搜索方法，包括最速下降、牛顿方法以及步长计算等 信赖域方法  *介绍信赖域求解最优化问题的思路 共轭梯度方法  *介绍共轭方法的思路 拟牛顿方法  *介绍拟牛顿方法，用一阶梯度近似Hessian矩阵方法 大规模无约束最优化方法  *大规模无约束问题，LBFGS等 梯度计算  *复杂函数梯度近似方法 无梯度最优化方法  *不计算梯度情况下，如何进行最优化 最小二乘问题  *最优化方法应用，求解最小二乘问题 非线性方程  *最优化方法应用，求解非线性方程问题 有约束最优化问题  *介绍等式、非等式约束最优化问题以及最优化条件，包括KKT条件、对偶等 线性规划问题  *线性规划常见求解算法 非线性约束最优化问题  *介绍非线性约束的最优化问题求解思路 二次规划问题  *目标函数是二次函数的特殊最优化问题，是SQP、内点等方法的基础 惩罚和增广拉格朗日方法  *求解带约束最优化问题常用方法 序列二次规划和内点法  *SQP和IP方法对于求解大规模约束最优化问题提供方案

Nelder–Mead algorithm ( NM算法 ）其实是一种非常简单易懂的适用于在线最优化的算法。。。总的来说这个算法有些无脑。。。

收敛速度慢，效果一般般，因为适用范围较广（或者说unconstrained optimization，无固定模型也可以）

核心就是：向着最优的解收敛，不断抛弃更新现有的解

简介：

　　n维空间中，由n+1个顶点，可以组成“最简单”的图形，叫单纯形。

　　NM算法就是先构造一个出师的，包含给定点的单纯形。

　　然后使用可能的三种手段（反射，扩展，压缩）去替换函数值最差的顶点。

　　在以上三种手段失效的时候，使用收缩。

　　直到该单纯形的半径足够的小。

　　（半径的定义可以有很多，比如两两点的距离，两两点构成的向量中最大的维度的值，

只要当“半径”趋近与0的时候，该单纯形趋于一个点即可）

以下来自wiki：

理解：

Reflection：以最优点为中心，做最差点的反射点，来达到抛弃最差点的目的。

Expansion：扩大最优点的优势，尝试是否能够得到更优的解。

Contraction：收缩搜索范围。

Shrink：整体向着最优解收缩。