二分图的概念:如果一个无向图能够被划分为两个集合,使得每一条边的两个端点都在不同的集合中。
下图就是一个二分图。
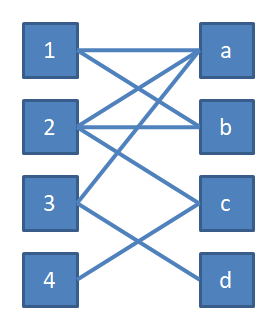
二分图的一个常见问题就是二分图匹配。匹配是指二分图中两两没有公共点的边集,最大匹配问题则是要求一个所含有的边最多的匹配。
POJ 1274 The Perfect Stall
题意简述:每只牛只会去它喜爱的牛棚产奶,一座牛棚只能容纳一只牛,求最多能有多少牛同时产奶。
很显然这就是一个求二分图最大匹配的问题,解决这类问题的算法之一就是匈牙利算法。我们还是以上图为例演示匈牙利算法。
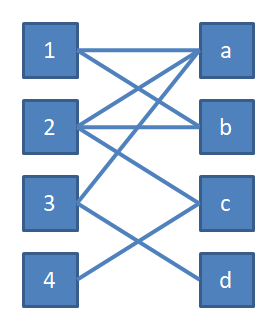
我们让左侧的节点表示牛,右侧的节点表示牛棚。
从 1 号开始,它可以去 a 牛棚,于是将其分配到a牛棚。
途中橙色的边表示匹配边,即在我们当前求出的匹配中的边;蓝色的线表示非匹配边。
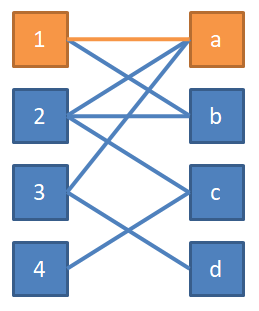
2 号也可以去 a 牛棚,但是 a 牛棚已经有 1 号牛了,为了让 2 号牛去 a 牛棚,我们需要让 1 号牛去别的地方。我们发现可以让 1 号改去 b 牛棚,2 号去 a 牛棚,这样我们就让两只牛都入住牛棚了。
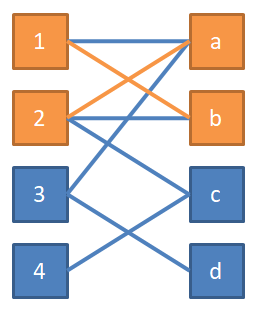
3 号也可以去 a 牛棚,但 a 牛棚现在又有 2 号牛了,同样我们需要让 2 号牛腾出地方。2 号牛还可以去 b 牛棚,递归查询 1 号牛,因为 1 号牛除了 a 和 b 牛棚已无处可去,因此让 2 号牛去 b 牛棚不可行。2 号牛还可以去 c 牛棚,于是让 2 号牛去 c 牛棚,3 号牛去 a 牛棚。
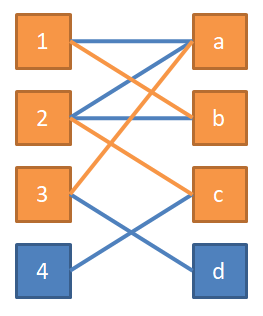
4 号可以去 c 牛棚,但 c 牛棚已经有 2 号牛了。查询 2 号牛,它还可以去 a 牛棚,但 a 牛棚又有 3 号牛;于是递归查询 3 号牛,它还可以去 d 牛棚,d 牛棚是空的。于是让 3 号牛去 d 牛棚,2 号牛去 a 牛棚, 4 号牛去 c 牛棚,皆大欢喜。

由此我们知道,这种算法的执行过程就是“腾”,尽可能让当前的牛可以去的牛棚能够腾空。
AC代码:
#include <cstdio> #include <algorithm> #include <cstring> #include <vector> using namespace std; int barn[1010]; //这一数组表示第i个牛棚中装了哪只牛 bool vis[1010]; //vis数组加速 int n,m; vector<int> cowwill[1010]; bool dfs(int cown){ for(auto i:cowwill[cown]){ if(vis[i]) continue; //若已被查询过,那么一定是不能腾出的 vis[i]=true; //否则应该已经回溯退出 if(!barn[i]||dfs(barn[i])){ //如果这一牛棚为空,或者该牛棚可以腾出空间 barn[i]=cown; //则将当前牛放入新的牛棚 return true; } } return false; } int main(){ int k,t,ans; while(scanf("%d%d",&n,&m)==2){ memset(barn,0,sizeof(barn)); for(int i=1;i<=n;i++) cowwill[i].clear(); //多测记得清零 ans=0; for(int i=1;i<=n;i++){ scanf("%d",&k); for(int j=0;j<k;j++){ scanf("%d",&t); cowwill[i].push_back(t); } } for(int i=1;i<=n;i++){ memset(vis,0,sizeof(vis)); if(dfs(i)){ ++ans; //如果这一只牛可以放进新的牛棚,则答案+1 } } printf("%d\n",ans); } return 0; }
在这里为了简洁,我们将没有与任何一条匹配边直接相连的点叫做未匹配点,其他的叫做匹配点。
注意我们最后一步访问的顺序,4(未匹配点) --非匹配边-- c --匹配边-- 2 --非匹配边-- a --匹配边-- 3 --非匹配边-- d(未匹配点),像这样的,从未匹配点开始,依次途经非匹配边、匹配边、非匹配边、匹配边、... 、非匹配边,最终到达另一个未匹配点的一条路径叫做增广路。
在完成最后一步后,这条路径则变成了 4 --匹配边-- c --非匹配边-- 2 --匹配边-- a --非匹配边-- 3 --匹配边-- d。从这可以引出一个结论:
在二分图中如果存在一条增广路,那么我们向这个匹配中添加这条路径上的所有非匹配边,删除这条路径上的所有匹配边,得到的新边集仍然时一个匹配,并且其中的边比原匹配多一条。
匈牙利算法的本质就是在找增广路,不断改进匹配。可以证明以下结论:
1. 如果二分图中不存在增广路,则当前匹配为最大匹配。
2. 在执行匈牙利算法的过程中,如果现在不能找到从某点开始的增广路,那么以后也找不到。
这两条结论保证了匈牙利算法的正确性。
匈牙利算法的时间复杂度应该是 O(mn).