这里所介绍的二分图匹配算办法又称之为匈牙利算法，而至于为什么被称为匈牙利算法，其原因只有一个，因为他是由一个匈牙利数学家Edmonds在1965年提出的一种算法。
>匈牙利算法是基于Hall算法中充分性证明的思想，是二分图匹配的最常见的算法，其算法的核心就是寻找增广路径，是一种用增广路求二分图最大匹配的算法。
——摘自《度娘百科》
首先我们来建立一个初步的认识：
1、什么叫做二分图呢？？
顾名思义，二分图就是被分成两块的图，是图论中的一种特殊模型。比如下图
我们暂且将这个图称为G=（Yeasion，Nein），这表示这个图被分为了两个集合，一个是左边的四个点，1，2，3，4属于Yeasion集合，而右面的A,B,C,D属于Nein集合。由于整张图被Yeasion和Nein两个集合给分取了，于是便叫做了二分图。
这就是一个还没有连边的二分图。而关于二分图的连边有一个特殊的性质：同集合内不能进行连线。换句话说，就是只能进行相异集合内元素的连接。
比如这么连：
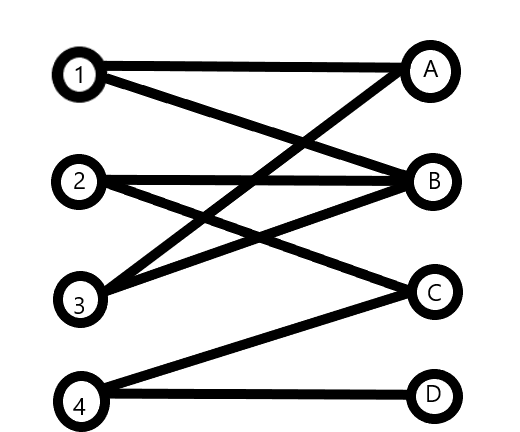
就是一种连法。
那么什么叫做匹配呢？？就是我们选取这几条边的其中几条，保证任意两条边都没有公共端点，比如选取（2，B）和（3，B）就不行，因为这两条边有一个公共端点B。比如下图就是该图的一个匹配。
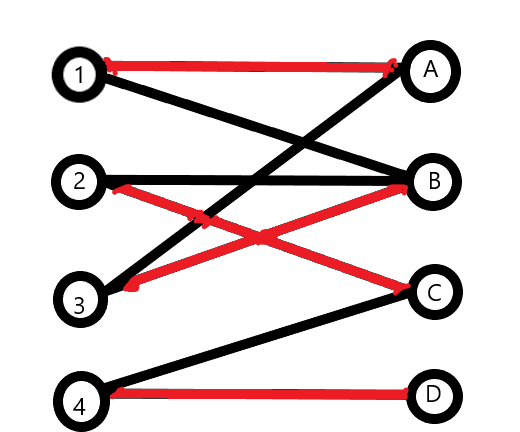（图丑见谅。。。。。qnq）
我们在这里面可以很容易的发现，你无法再找出一个匹配方法的符合法则的边的数量超过这个图。因为一共有八个点，我们最多找到四条边。此时，这个图的匹配方法就被称为该二分图G的最大匹配。
以上介绍了两个基本概念：匹配与最大匹配。
接下来再介绍几个定义：
1.完全匹配。
就是某些文章中所说的完备匹配，就是要让所有的点都有连边。就是每一个端点都被匹配。以上这个图中是有最大匹配的，但是不一定每一个二分图中都有。所以要依情况而定。一个很浅显的道理:二分图完全匹配中的边数=端点数/2。
2.最优匹配。
这听起来好像和最大匹配并没有什么区别，但是要注意：最有匹配是带权的匹配，不一定要使得连的边数最多，但是要使你连的所有边的权值最大。
并且最优匹配也是一个完全匹配。注意一个点：当两个集合的元素个数不相等的时候，可以通过补上点，并添加权值为0的边。
3.最小覆盖
分为最小顶点覆盖和最小路径覆盖。
最小顶点覆盖，是指的用最少的顶点数使每一条边都至少与其中的一个点关联，二分图的最小顶点覆盖数=二分图最大匹配数。
最小路径覆盖，就是用尽量少的边（不相交的简单路径）覆盖二分图里面的所有顶点。二分图的最小路径覆盖数=二分图的顶点数-二分图最大匹配数。
4.最大独立集
就是寻找一个点最多的集合，是的这个集合中的任意两个点在图中都没有边相连。二分图的最大独立集=二分图最小路径覆盖数。
So，正式开始我们的匈牙利算法。
首先，我们建立一个图，来做一个匈牙利算法的模拟流程。
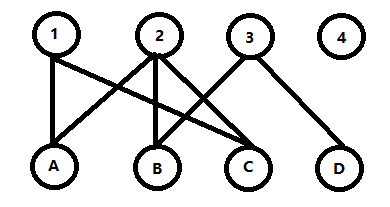
那么我们现在知道了集合Yeasion是有{1,2,3,4}，Nein是有{A,B,C,D}。
然后题目就是让我们输出这个图的最大匹配数，我们首先记一个ans用以记录最大匹配数。
首先从A开始，我们发现有{A，1}，和{A，2}，我们先取第一个，然后就匹配上了{A，1}.
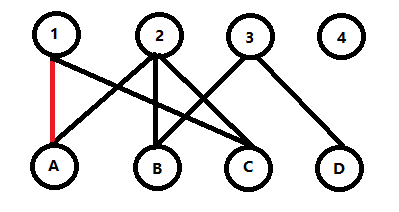
然后继续进行，我们循环到发现了B，然后发现B有{B，2}和{B，3}两个边，所以我们仍然先匹配{B，1}.
然后我们继续进行便利，发现C一共有两个相连的边，分别为{C，1}和{C，2}，按照我们的规则，取第一个匹配。
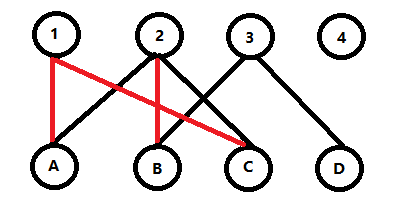
但是我们发现，他违背了第一个法则：二分图中没有任何一条边有公共的端点。而我们如果这样进行匹配，{A，1}和{C，1}就有了公共端点1.
于是我们在这里进行回溯操作。
我们由C找到1，然后发现1已经连上了A，于是破坏掉{A，1}的匹配，加上{C，1}的匹配，然后回溯到A。
既然1已经被后来居上的C给无耻占领了，然后我们继续对A进行搜索，发现A还有{A，2}这条边，于是我们再次连上这条边。
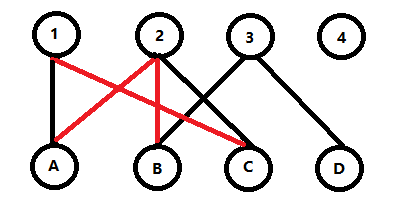
但是我们再次发现，{A,2}和{B,2}又再次冲突了，于是我们再次执行回溯操作。
我们由A找到2，然后发现2已经连上了B，于是破坏掉{B，2}的匹配，加上{A，2}的匹配，然后回溯到B。
我们发现B还有一个可连的3，于是我们连接上{B，3}.
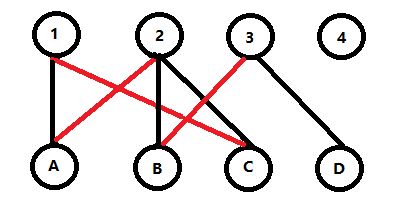
然后我们接着遍历，到了D，发现，我们用上面的遍历方法，无法使得D再次有边。那么遍历就此结束。
那么上面就是基本的匈牙利算法流程。