【洛谷】P1306 斐波那契公约数

闲来无事，开始刷洛谷。这是一道与斐波那契数有关的题。

原题链接：https://www.luogu.com.cn/problem/P1306

分析：

直接上递归方式求Fibonacci数列的公式，发现全部TLE（微笑）。

发现这题并没有那么简单（毕竟是省选题）。

查阅资料：

①矩阵递推关系

由线性代数知识得，下面这个式子是成立的：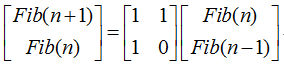

不停地利用这个式子迭代右边的列向量，会得到下面的式子：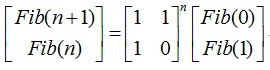

这样，问题就转化为如何计算这个矩阵的n次方了。

②矩阵快速幂

考虑直接计算矩阵A的n次幂，需要算n次。时间复杂度为O(n)。有没有更快的方法？

快速幂是一种利用结合律快速计算幂次的方法。比如我要计算 $2^{20}$ ，我们知道 $2^{20} = 2^{16} * 2^{4}$ ，而 $2^{2}$ 可以通过 $2^{1} \times 2^{1}$ 来计算， $2^{4}$ 而可以通过 $2^{2}\times 2^{2}$ 计算，以此类推。通过这种方法，可以在O（logn）的时间里计算出一个数的n次幂。快速幂的代码如下：

int QuickPow(int a,int n){
    int ans=0;
    while(n){
        if(n&1)ans*=a;
        a*=a;
        n>>=1;
    }
    return ans;
}

同样的，对矩阵运算也可以采用相同的套路。

③发现对于Fibonacci，有一个公式是成立的：gcd(fibonacci(m),fibonacci(n))=fibonacci(gcd(m,n))

证明

Part 1

gcd(Fn,Fn−1)=1
证明：gcd(Fn,Fn−1)=gcd(Fn−Fn−1,Fn−1)=gcd(Fn−2,Fn−1)gcd(Fn,Fn−1)=gcd(Fn−Fn−1,Fn−1)=gcd(Fn−2,Fn−1)……
归纳得证

Part 2

Fn+m=Fn−1Fm+FnFm+1
首先对于m=1显然成立
对于m=2推一下也成立
然后我们来归纳一发，若m=k-1和m=k成立，那么m=k+1也成立
Fn+k+1=Fn+k+Fn+k−1
=Fn−1Fk+FnFk+1+Fn−1Fk−1+FnFk
=Fn−1(Fk+Fk−1)+Fn(Fk+1+Fk)
=Fn−1Fk+1+FnFk+2
得证

Part 3

gcd(Fn+m,Fn)=gcd(Fn,Fm)
证明：gcd(Fn+m,Fn)=gcd(Fn−1Fm+FnFm+1,Fn)=gcd(Fn−1Fm,Fn)=gcd(Fm,Fn)//因为Fn-1与Fn互质
得证

Part 4

gcd(Fn,Fm)=Fgcd(n,m)gcd(Fn,Fm)=Fgcd(n,m)
Part 3 的结论也可以写作gcd(Fn,Fm)=gcd(Fn−m,Fm)gcd(Fn,Fm)=gcd(Fn−m,Fm)

gcd(Fm,Fn)=gcd(Fm,F(n mod m)),继续递归即可证明。

④那么就可以愉快的写代码了：

#include<iostream>
using namespace std;
#define ll long long
ll fibo(int n);
ll gcd(int m, int n);
struct matrix {
    ll m[2][2];
}ans, base;
matrix multi(matrix a, matrix b);

int main() {
    int m, n;
    cin >> m >> n;
    ll out = fibo(gcd(m, n));
    cout << out;
}

ll fibo(int n) {
    ans.m[0][1] = ans.m[1][0] = 0; ans.m[0][0] = ans.m[1][1] = 1;
    base.m[0][0] = base.m[0][1] = base.m[1][0] = 1; base.m[1][1] = 0;
    while (n) {
        if (n & 1)ans = multi(ans, base);
        base = multi(base, base);
        n >>= 1;
    }
    return ans.m[1][0];
}

ll gcd(int m, int n) {
    while (m != n) {
        if (m > n)m -= n;
        else n -= m;
    }
    return m;
}

matrix multi(matrix a, matrix b) {
    matrix t;
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            t.m[i][j] = 0;
            t.m[i][j] =(a.m[i][0] * b.m[0][j] + a.m[i][1] * b.m[1][j])%100000000;//该题要求模10e8，故这里这么写。否则会溢出。
        }
    }
    //cout << t.m[0][0] << " " << t.m[0][1] << " " << t.m[1][0] << " " << t.m[1][1] << endl;
    return t;
}

参考：

1^ 斐波那契数列当n很大时如何高效的求借第n项a(n) mod M的值? - 王希的回答 - 知乎

https://www.zhihu.com/question/23582123/answer/40464211

2^ 定理证明 https://blog.csdn.net/alan_cty/article/details/73928751

3^官方题解https://www.luogu.com.cn/problemnew/solution/P1306

【洛谷】P1306 斐波那契公约数

猜你喜欢