(四)数据分布的数字特征
数据的分布特征与使用的描述统计量

数据集中趋势
在统计研究中,需要搜集大量数据并对其进行加工整理,大多数情况下数据都会呈现出一种钟形分布,即各个变量值与中间位置的距离越近,出现的次数越多;与中间位置距离越远,出现的次数越少,从而形成了一种以中间值为中心的集中趋势。这个集中趋势是现象共性的特征,也是现象规律性的数量表现。
根据统计学知识,集中趋势指平均数,是一组数据中有代表性的值,这些数值趋向于落在数值大小排列的数据中心,被称为中心趋势度量。最常用的中心趋势度量有算术平均数、几何平均数、调和平均数、众数和中位数。
均值是一组数据的算术平均,它利用了全部数据信息,是概括一组数据最常用的一个值。
众数是一组数据中出现次数最多的变量值,它用于对分类数据的概括性度量,其特点是不受极端值的影响,但它没有利用全部数据信息,而且还具有不唯一性。一组数据可能有众数,也可能没有众数;可能有一个众数,也可能有多个众数。
中位数是一组数据按大小顺序排序后处于中间位置上的变量,它主要用于对顺序数据的概括性度量。
对于总体中的个体数据,有时会呈现出在一定范围内以某个数据为中心上下波动的分布特征,即数据有时具有它分布的中心,我们称之为数据分布的集中趋势。
集中趋势指标的分类

集中趋势指标的作用
可以反映一组数据分布的中心或一般水平;
可以反映同一现象在不同时间或空间条件下的发展趋势或差异;
以用来分析现象之间的依存关系;
样本平均数是统计推断的一个重要统计量。
集中趋势的测定
数值平均数
数值平均数只适用于定量数据(数值型数据),而不适用于定性数据。
1、算术平均数
(1)简单算术平均数
简单算术平均数是根据未分组数据(原始数据)计算的一种平均数,它是将所有的原始数据相加再除以数据总个数得到的。
- 样本计算的简单算术平均数的计算公式是:
- 总体数据计算的简单算术平均数的计算公式为:
2、加权算术平均数
- 加权算术平均数是根据分组数据计算的一种平均数。设样本被分为k组,各组的频数为fi样本计算的加权算术平均数的计算公式为:

其中,Xi有两种情况:在单变量值分组中,Xi代表各组的变量值;在组距式分组中,Xi代表各组的组中值,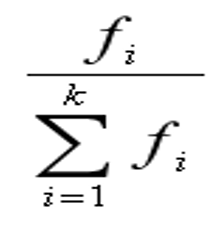 称作权重(频率)。
称作权重(频率)。
- 总体数据计算的加权算术平均数 的计算公式为:

(3)算术平均数的主要数学性质
①各变量值与其算术平均数的离差之和等于零;
即: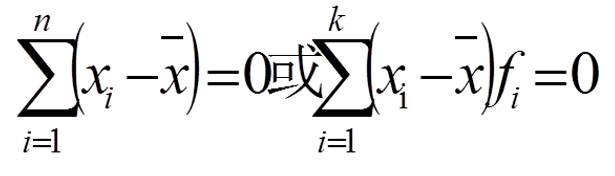
②各变量值与其算术平均数的离差平方和最小。
即: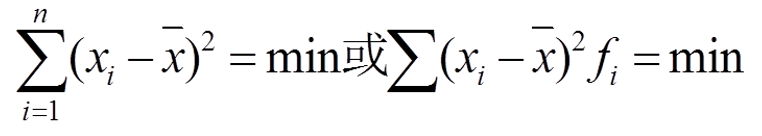
3. 调和平均数
调和平均数加权算术平均数的一种变形。
调和平均数与加权算术平均数的关系是:若已知各组变量值 及其标志总量mi(mi=xifi ),而缺乏fi的数据时,则加权算术平均数可通过变形得到fi(fi=mi/xi)后,再以mi为权数的调和平均数形式来计算。

4. 几何平均数
几何平均数是 n个变量值连乘积的n次方根
(1)简单几何平均数
当样本数据中各变量值出现的次数都相同时,用简单几何平均数公式。
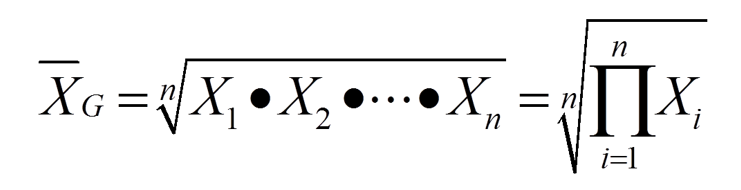
式中,xi代表各变量值,n为样本容量, 为连乘符号
(2)加权几何平均数
当样本数据中各变量值出现的次数不全相同时,用加权几何平均数公式。

式中,xi代表各变量值,n为样本容量, 为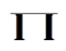 连乘符号
连乘符号
如果获得一组总体数据,根据总体数据计算的几何平均数 的公式与样本数据的基本相同。
需要注意的是:
- 当数据中出现零或负值时不宜计算几何平均数;
- 几何平均数是一种适用于特殊数据的平均数,当变量值之间具有连乘积关系时,采用几何平均数更加合理;
- 现实生活中,几何平均数主要用于计算现象的平均增长率和平均发展速度。
统计学计算题选讲: https://blog.csdn.net/seagal890/article/details/105498085
位置代表值
1. 众数
众数(Mode)是一组数据中出现频数最多的变量值,通常用符号 表示。
众数主要用于测度分类数据的集中趋势,也可作为顺序数据以及数值型数据集中趋势的测度值。
众数代表的是最常见、最普遍的情况。众数不仅可以度量定性数据的集中趋势,还可以度量定量数据的集中趋势。
众数的特点:
- 众数是位置型平均数,它只与位置有关,不受数据中极端值的影响;
- 从分布形态上看,众数是一组数据分布最高峰点所对应的变量值;
- 众数具有不唯一性(可以有一个或多个或没有)

组距式分组数据中众数的求解较为复杂。在组距式分组数据中,求解众数的步骤:
- 先要确定众数所在组;
如果是等距分组数据,那么次数最多的那一 组就为众数组;如果是不等距分组数据,那么组密度(组频率/组距)最大的组就为众数组。
- 之后再按照下列公式求解众数的近似值。计算公式如下:
下限公式:

上限公式:
![]()

2. 中位数
中位数是一组数据从小到大排序后位于中间位置上的变量值,通常用符号 表示。
由于中位数和位置有关,所以中位数只能度量定序数据和数值型数据的集中趋势;
求解中位数的步骤:
- 首先,对数据进行排序;
- 其次,确定中位数的位置,即中间位置;
- 最后,计算中间位置上的变量值。
中位数的位置计算公式为:

分组数据中位数的求解
对于分组数据而言,不需要再另外排序,直接按照分组的顺序即可。
分组数据中位数的位置计算公式:

求出中位数位置后,按照下列公式求解中位数的近似值。
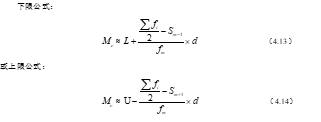
中位数特点及应用
- 中位数是位置型度量值,其特点是不受极端值的影响,因此具有稳定性;
- 在实际运用中,当数据的偏斜程度较大时,用中位数作为该组数据一般水平的代表值比较合适。
3. 分位数
实际上,测度数据在特定位置上的水平,还可以计算四分位数、十分位数和百分位数等,我们统称它们为分位数 。
四分位数
定义:一组数据由小到大排序后位于25%位置和75%位置处的变量值。
位于在25%位置处的变量值(即下四分位数,用符号QL表示)和处在75%位置处的变量值(即上四分位数,用符号QU表示),上、下四分位数之间恰好包含了50%的数据。
求解四分位数的步骤:
- 先排序;
- 然后确定上、下四分位数的位置;
- 最后,求相应位置上的变量值。(看例题P69)
![]()
4. 箱线图
将中位数、四分位数和其他指标结合起来,可以更详细的反应数据的分布特征。
箱线图是由一组数据的最小值(Xmin)、最大值(Xmax)、下四分位数(QL)、上四分位数(QU)和中位数(Me)这五个特征值构成。通过箱线图,可以观察数据的中心位置、离散程度及对称性等特征,同时还可以进行多组数据分布的比较。

算术平均数、众数和中位数三者的比较与应用
(1)算术平均数属于数值型平均数,它是根据全部数据计算的集中趋势测度值,因此可以综合反映全部数据的信息;众数和中位数属于位置型代表值,它们是根据数据分布的特定位置确定出的集中趋势测度值,因此不能概括全部数据的信息
(2)算术平均数和中位数在任何一组数据中都存在且具有唯一性,但不一定所有数据都存在众数,且众数也不具有唯一性。一般情况下,在数据量充分大并且具有明显集中趋势时,计算众数才有意义;
(3)算术平均数只适用于定量数据,中位数适用于定序数据和定量数据,众数则适用于所有数据,即定性数据和定量数据均可;
(4)算术平均数受极端值的影响,因此,当数据偏斜程度较大时(数据中存在极端值),不宜用算术平均数来代表数据的一般水平。众数和中位数不受极端值的影响,因此,当数据偏斜程度较大时,可以考虑用众数或中位数来代表数据的一般水平;
(5)算术平均数可以估计或推断总体特征值。而众数和中位数不宜用作此类推断
(6)算术平均数和众数、中位数的数量关系主要取决于数据分布的偏斜程度(非对称程度)
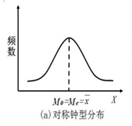
- 对于呈现单峰分布的数据,如果数据的分布是对称的,则众数M0、中位数Me和算术平均数X三者相等,即M0=Me=X
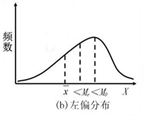
- 如果数据呈现左偏(负偏)分布,说明数据中存在极小值
从而略使中位数偏小,而众数则完全不受极小值大小和位置的影响,因此一般情况下,三者的关系表现为X<Me<M0
- 如果数据呈现右偏(正偏)分布,则一般有:M0<Me<X
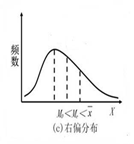
(7)皮尔逊经验公式数据呈现偏斜但偏斜程度不大时,算术平均数、众数和中位数之间存在一定的比例关系,即
![]()
数据离散程度的测定
离散程度测定问题的提出
由于差异性是数据的本质属性,所以各个数据与其分布中心之间总是存在着不同程度的偏离。我们把数据偏离其中心值的程度叫做离散程度,离散程度可以说明数据之间差异程度的大小,那么如何测定一组数据的离散程度呢?
离散程度测定的作用
离散程度的大小主要通过变异指标来测定。变异指标的主要作用有:
- 可以衡量平均指标的代表程度。变异指标值越大,则数据的离散程度越大、数据越分散,继而平均指标的代表性就越弱;反之,变异指标值越小,则数据的离散程度越小、数据越集中,继而平均指标的代表性就越强;
- 可以反映数据的稳定性和均衡性。变异指标值越大,则数据的离散程度越大,数据的稳定性和均衡性就越差;反之,则数据的离散程度越小,数据的稳定性和均衡性就越好。
离散程度的测定
离散程度的测定,可以采用异众比率,极差、四分位差或者平均差等。
异众比率
异众比率是指非众数组的频数占总频数的比重,通常用Vr表示,计算公式为:
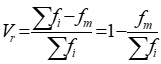
式中: ![]() 是众数组的频数;
是众数组的频数; ![]() 是变量值的总频数
是变量值的总频数
异众比率的特点:
- 可用来衡量众数的代表性强弱,即,异众比率越大,则众数的代表性越弱;反之,众数的代表性就越强;
- 异众比率主要用于测度定性数据的离散程度,也可以用于定量数据离散程度的测度。
极差、四分位差和平均差
极差
极差(Range)又称全距,是一组数据中最大值与最小值之差,通常用R表示。计算公式为:
![]()
- 对于原始数据和单变量值分组数据:
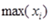 为一组数据的最大值;
为一组数据的最大值; 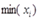 为一组数据的最小值。
为一组数据的最小值。 - 对于组距式分组数据,极差就用变量值最大组的上限减去变量值最小组的下限近似得到。
极差的特点:极差是变异指标中最简单的测度值,其优点是计算简便、易于掌握。但因极差只利用了一组数据两端的信息,容易受到极端值的影响。因此,极差不能全面、稳定地反映数据的离散程度。
四分位差
四分位差是指上四分位数(QU)与下四分位数(QL)之差,因此也叫内距或四分间距。
计算公式为:
![]()
四分位差特点:
- 四分位差只能说明中间50%数据的离散程度,它依然不能充分反映全部数据的离散状况。四分位差越大,说明中间50%数据的离散程度越大;四分位差越小,说明中间50%数据的离散程度越小;
- 在一定程度上,四分位差也可以反映中位数的代表性好坏;
- 四分位差是一种顺序统计量,因此四分位差适用于测度定序数据和定量数据的离散程度。
平均差
平均差(mean deviation)是各变量值与其算术平均数离差绝对值的平均数。因此,也称平均绝对离差,通常用M.D表示。
平均差的计算有两种情况
- 简单平均法
如果数据是未分组数据(原始数据),则用简单算术平均法来计算平均差:

- 加权平均法
如果数据是分组数据,采用加权算术平均法来计算平均差:
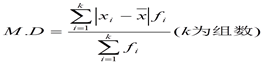
平均差的特点:
- 平均差意义明确,计算结果易于理解,并且利用了全部数据的信息,反映了每个变量值与平均数的平均差异程度。因此能全面地反映一组数据的离散状况。平均差越大,则数据的离散程度越大;平均差越小,则数据的离散程度越小;
- 为了避免正负离差相互抵消的现象发生,平均差在计算时给离差加上了绝对值。但由于绝对值的出现给计算带来了很大的不便,因此在实际应用中受到很大的限制。
方差和标准差
方差是各变量值与其算术平均数离差平方的算术平均数。标准差就是方差的平方根。
方差、标准差特点:
- 方差、标准差利用了全部数据的信息,能较好地反映数据的离散程度;
- 方差、标准差是通过平方的方法消去离差的正负号,这更便于数学上的处理。因此,方差、标准差是统计中最重要的变异指标,同时也是实际中应用最广泛的离散程度测度值。
方差、标准差计算公式
总体数据

样本数据
① 未分组数据(原始数据)的样本方差和样本标准差的计算公式分别为:
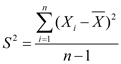
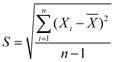
② 分组数据的样本方差和样本标准差的计算公式分别为:
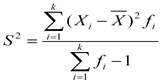

(k为组数)
标准化值(标准分数)
标准化值就是用各变量值与其平均数的离差再除以其标准差。
标准化值的计算公式为:
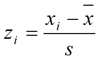
标准化值的特点:标准化值具有均值为0,标准差为1的特性。
经验法则(3σ 质量管理法则的原理)
使用条件:
在正态分布或近似正态分布(对称的钟型分布)的条件下
- 大约有68%的数据位于均值±1个标准差范围内;
- 大约有95%的数据位于均值±2个标准差范围内;
- 大约有99%的数据位于均值±3个标准差范围内。
切比雪夫定理
利用切比雪夫定理来判断有多少的数据落入以均值为中心的k(标准化值)个标准差范围内。
使用条件:任意分布形态的数据
根据切比雪夫定理的内容,至少有(![]() )的数据落入均值左右k个标准差范围内,其中k为大于1的任意数,当然也可以为小数。
)的数据落入均值左右k个标准差范围内,其中k为大于1的任意数,当然也可以为小数。
- k=2 说明至少有75%的数据落入均值±2个标准差范围内;
- k=3 说明至少有89%的数据落入均值±3个标准差范围内;
- k=4 说明至少有94%的数据落入均值±4个标准差范围内。
离散系数
离散系数也称变异系数(coefficient of variation),它是极差、四分位差、平均差或标准差等变异指标与其算术平均数对比的结果。
常用的离散系数有极差系数、平均差系数和标准差系数,但应用最广泛的是标准差系数。
标准差系数的计算公式:

离散系数的作用
离散系数是测度数据离散程度的相对统计量,可用于比较不同变量值水平或不同计量单位的不同组别数据的离散程度。
离散系数大的,则该组数据的离散程度就大;离散系数小的,则该组数据的离散程度就小。
总结:反映数据离散程度的各测定值的应用场合
1)对于分类数据,主要用异众比率来测度其离散程度;
2)对于顺序数据,主要用四分位差来测度其离散程度;
3)对于数值型数据,主要用方差或标准差来测度其离散程度。
4)当需要对不同组别数据的离散程度进行比较时,则使用离散系数。
数据分布形态的测定
分布形态测定问题的提出
集中趋势和离散程度是数据分布特征的两个重要方面,但要想全面了解数据的分布特点,我们还需要知道数据的分布形状,那么如何测定一组数据的分布形状呢?
分布形态测定的作用
通过分布形态的测定,我们可以了解数据分布形状的对称性以及分布曲线的扁平陡峭程度。将这两点结合,我们还可以判断数据是否接近于正态分布。
矩
数据分布形态的测度主要是通过偏度系数和峰度系数来实现的。矩又是计算偏度系数和峰度系数的基础。
矩可分为总体矩和样本矩。
样本距
一般来说,将一组样本X1,…,Xn与其算术平均数离差的k次方的平均数称为样本的k 阶中心矩,即


算术平均数: 一阶原点矩
方差 : 二阶中心矩
阶数k=3和k=4时,矩则可以反映数据的分布形态特征。矩可以看成是一系列反映数据分布特征指标的统称。
偏度
偏度(skewness)是指数据分布的不对称程度或偏斜程度。偏度也就是对数据非对称程度和方向的测度。用来测定偏度的统计量是偏度系数,记作SK 。
对于分组数据,偏度系数SK 的计算公式为:

其中,为样本的3阶中心距,
为样本标准差的三次方。
偏态系数性质:
- 如果分布是对称的,则SK=0;
- 如果SK≠0,说明分布是非对称的;当SK>0时,表明分布是右偏分布(正偏分布);当SK<0时,表明分布是左偏分布(负偏分布)。SK的数值越大,表明数据的偏斜程度越大。
峰度
1、峰度(kurtosis)是指数据分布曲线的陡峭或扁平的程度。
2、对峰度的度量通常以正态分布曲线为标准进行比较。如果比正态分布曲线更加尖峭,称为尖峰分布;如果比正态分布曲线更加扁平,称为扁平分布。
3、测度峰度的统计量是峰度系数,记作K。对于分组数据,峰度系数K 的计算公式为:

其中,为样本的4阶中心距,
为样本标准差的四次方。
4、峰态系数性质:
- 当K=0 时,说明分布为正态分布;
- 当K>0 时,说明曲线是尖峰(陡峭)分布,即数据比正态分布更集中,K的数值越大,则曲线越陡峭;
- 当K<0 时,说明曲线是扁平分布,即数据比正态分布更分散, K的数值越小,则曲线越平缓。
