数据结构---图（Graph）

定义和相关术语

• 图由顶点（Vertex）和边（Edge）组成，每条边的两端都必须是图的两个顶点（可以是相同顶点）。记G（V,E）。

• 顶点：图中的数据元素。

• 弧：若 <v, w>∈E，则 <v, w> 表示从 v 到 w 的一条弧，且称 v 为弧尾，称 w 为弧头，此时的图称为有向图。

• 边：若 <v, w>∈E 必有<w, v>∈E，则以无序对 (v, w) 代表这两个有序对，表示 v 和 w 之间的一条边，此时的图称为无向图。

• 顶点和边都可以有一定属性，量化的属性称为权值，顶点的权值和边的权值称为点权或边权。

• 图可以分为有向图和无向图，可以把无向图的所有边看成是双向边。

• 特点：
  图的任意两个顶点之间都可能相关；
  顶点之间的关系是任意的；
  顶点的前驱和后继个数无限制；

• 无向图中边的取值范围：0≤e≤n(n-1)/2。
  有向图中弧的取值范围：0≤e≤n(n-1)。

• 完全无向图：有 n(n-1)/2 条边的无向图，即：每两个顶点之间都存在着一条边。
  完全有向图：有 n (n - 1) 条弧的有向图 ，即：每两个顶点之间都存在着方向相反的两条弧。

• 稀疏图：含有很少条边或弧的图。
  稠密图：含有很多条边或弧的接近完全图的图。

• 权：与图的边或弧相关的数，这些数可以表示从一个顶点到另一个顶点的距离或耗费。
  网： 带权的图。

• 子图：如果图 G = (V, E) 和 G´= (V ´, E´)，满足：V ´属于V 且 E´属于E，则称 G´为G 的子图。

• 邻接点：若 (v, v´) 是一条边，则称顶点 v 和 v´互为邻接点，或称 v 和 v´相邻接；称边 (v, v´) 依附于顶点 v和 v´，或称边 (v, v´) 与顶点 v 和 v´ 相关联。
  若 <v, v´> 是一条弧，则称顶点 v 邻接到 v´，顶点v´邻接自顶点 v。并称弧 <v, v´> 与顶点 v 和 v´ 相关联。

• 度：无向图中顶点 v 的度是和 v相关联的边的数目，记为：记为：ID(v)。
  入度：有向图中以顶点 v 为头的弧的数目称为 v 的入度， 记为：ID(v)。
  出度：有向图中以顶点 v 为尾的弧的数目称为 v 的出度， 记为：OD(v)。
  度：入度和出度之和，即：TD(v) = ID(v) + OD(v)。
  有向图中所有顶点的入度之和等于所有顶点的出度之和。
  如果顶点 vi 的度为 TD(vi)，则一个有 n 个顶点 e 条 边（弧）的图，满足如下关系：e=1/2[TD（v1）+···+TD（vn）];

• 路径：从顶点 v 到 v´ 的路径是一个顶点序列 (v = vi, 0, vi, 1, …, vi, m= v´)
  对于有向图，路径也是有向的。
  路径长度：路径上边或弧的数目。
  回路（环）：第一个顶点和最后一个顶点相同的路径。
  简单路径：序列中顶点（两端点除外）不重复出现的路径。
  简单回路（简单环）：前后两端点相同的简单路径。
  连通：从顶点 v 到 v´ 有路径，则说 v 和 v´ 是连通的。
  连通图：图中任意两个顶点都是连通的。
  非连通图：有 n 个顶点和小于 n-1 条边的图。
  连通分量：无向图的极大连通子图（不存在包含它的更大的连通子图）；任何连通图的连通分量只有一个，即其本身；非连通图有多个连通分量（非连通图的每一个连通部分）。
  强连通图： 任意两个顶点都连通的有向图。
  强连通分量：有向图的极大强连通子图；任何强连通图的强连通分量只有一个，即其本身；非强连通图有多个强连通分量。
  -生成树：所有顶点均由边连接在一起但不存在回路的图。
  一个图可以有许多棵不同的生成树。
  所有生成树具有以下共同特点：
  生成树的顶点个数与图的顶点个数相同；
  生成树是图的极小连通子图；
  一个有 n 个顶点的连通图的生成树有 n-1 条边；
  生成树中任意两个顶点间的路径是唯一的；
  在生成树中再加一条边必然形成回路。
  含 n 个顶点 n-1 条边的图不一定是生成树。

• 生成森林：对于非连通图，其每个连通分量可以构造一棵生成树，合成起来就是一个生成森林。
  有向树：如果一个有向图恰有一个顶点的入度为 0 ,其余顶点的入度均为 1 ，则是一棵有向树。
  有向图的生成森林：由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。

图的存储结构

邻接矩阵

• 邻接矩阵是表示顶点之间相邻关系的矩阵。设G=(V,E)是具有n个顶点的图，顶点编号依次为0、1、…、n-1，则G的邻接矩阵是具有如下定义的n阶方阵A：
  

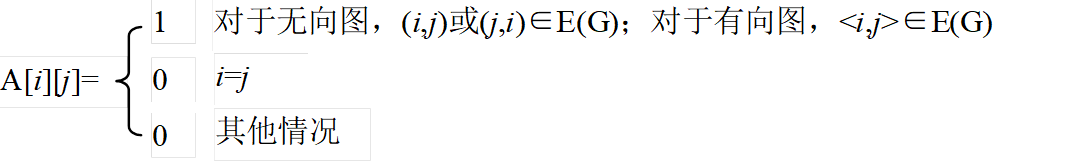
• 若G是带权图或网，则邻接矩阵可定义为（其中wij为边(i,j)或<i,j>的权）：
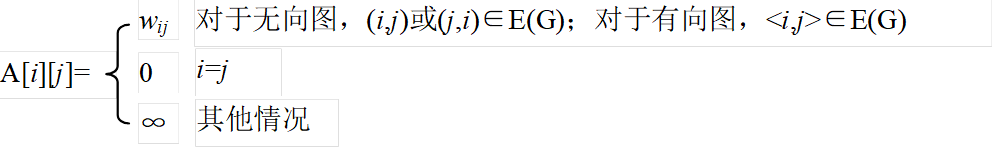
  无向图时一定为对称矩阵
  有向图不一定是对称矩阵

• 特点
  无向图的邻接矩阵对称，可压缩存储：有n个顶点的无向图所需存储空间为n(n-1)/2。
  有向图的邻接矩阵不一定对称：有n个顶点的有向图所需存储空间为n*n，用于稀疏图时空间浪费严重
  有向图中，顶点vi的出度是邻接矩阵中第i行1的个数，顶点vi的入度是邻接矩阵中第i列1的个数。

• 优点
  容易实现图的操作。
  缺点
  空间效率差，只适用于顶点数目不太大的图。

• 存储结构

#define MAXVEX 100		//图中最大顶点个数
typedef char VertexType[10];	//定义VertexType为字符串类型
typedef struct vertex
{   int adjvex;			//顶点编号
　　	VertexType data; 		//顶点的信息
} VType;			//顶点类型
typedef struct graph
{  int n,e;			//n为实际顶点数,e为实际边数
　　VType vexs[MAXVEX];		//顶点集合
　　int edges[MAXVEX][MAXVEX];	//边的集合
} MatGraph;				//图的邻接矩阵类型

• 建立图的邻接矩阵运算算法，由邻接矩阵数组A、顶点数n和边数e建立图G的邻接矩阵存储结构。

void CreateGraph(MatGraph &g,int A[][MAXVEX],int n,int e)
{　  int i,j;
　　g.n=n; g.e=e;
　　for (i=0;i<n;i++)
	for (j=0;j<n;j++)
	　　g.edges[i][j]=A[i][j];
}

• 销毁图运算算法，这里邻接矩阵是图的一种顺序存储结构，其内存空间是由系统自动分配的，在不再需要时由系统自动释放其空间。所以对应的函数不含任何语句。

void DestroyGraph(MatGraph g)
{  }

• 输出图运算算法，将图G的邻接矩阵存储结构输出到屏幕上。

void DispGraph(MatGraph g)
{　  int i,j;
　　for (i=0;i<g.n;i++)
　　{	for (j=0;j<g.n;j++)
	　　if (g.edges[i][j]<INF)
		　printf("%4d",g.edges[i][j]);
	　　else
		　printf("%4s","∞");
	printf("\n");
　　}
}

• 添加一个顶点运算算法，在图G中自动增加一个顶点，图中顶点是自动编号的。

void AddaVex(MatGraph &g)
{
　　g.n++;
}

• 插入边运算算法，在图G中添加一条从顶点u到v、权值为w的边，这一功能对于无向图和有向图略有不同。

int InsertEdge1(MatGraph &g,int u,int v,int w)	//无向图中插入边
{　   if (u<0 || u>=g.n || v<0 || v>=g.n)
　　　　return 0;			//顶点编号错误返回0
　　g.edges[u][v]=w;
　　g.edges[v][u]=w;
　　g.e++;				//边数增1
　　return 1;
}
int InsertEdge2(MatGraph &g,int u,int v,int w)	//有向图中插入边
{      if (u<0 || u>=g.n || v<0 || v>=g.n)
	return 0;			//顶点编号错误返回0
　　g.edges[u][v]=w;
　　g.e++;				//边数增1
　　return 1;
}

• 求顶点度运算算法，对于无向图和有向图，求顶点度有所不同。

int Degree1(MatGraph g,int v)	//求无向图中顶点的度
{      int i,d=0;
　　if (v<0 || v>=g.n)
	return -1;		//顶点编号错误返回-1
　　for (i=0;i<g.n;i++)
	if (g.edges[v][i]>0 && g.edges[v][i]<INF)
	　　d++;	//统计第v行既不为0也不为∞的边数即度
　　return d;
}
int Degree2(MatGraph g,int v)	//求有向图中顶点的度
{      int i,d1=0,d2=0,d;
　　if (v<0 || v>=g.n)
	return -1;	//顶点编号错误返回-1
　　for (i=0;i<g.n;i++)
	if (g.edges[v][i]>0 && g.edges[v][i]<INF)
	　　d1++;	//统计第v行既不为0也不为∞的边数即出度
　　for (i=0;i<g.n;i++)
	if (g.edges[i][v]>0 && g.edges[i][v]<INF)
	　　d2++;	//统计第v列既不为0也不为∞的边数即入度
　　d=d1+d2;
　　return d;
}

邻接表

• 若无向图中有 n 个顶点、e 条边，则其邻接表需 n 个头结点和 2e 个表结点。适宜存储稀疏图。
• 无向图中顶点 vi 的度为第 i 个单链表中的结点数。
• 邻接表
  顶点 vi 的出度为第 i 个单链表中的结点个数。
  顶点 vi 的入度为整个单链表中邻接点域值是 i的结点个数。
  逆邻接表
  顶点 vi 的入度为第 i 个单链表中的结点个数。
  顶点 vi 的出度为整个单链表中邻接点域值是 i的结点个数。
• 存储结构

typedef char VertexType[10];	//定义VertexType为字符串类型
typedef struct edgenode
{      int adjvex;			//邻接点序号
　　int weight;			//边的权值
　　struct edgenode *nextarc;	//下一条边的顶点
} ArcNode;		//每个顶点建立的单链表中边结点的类型
typedef struct vexnode
{      VertexType data;		//存放一个顶点的信息
　　ArcNode *firstarc; 		//指向第一条边结点
} VHeadNode;			//单链表的头结点类型
typedef struct 
{      int n,e;			//n为实际顶点数,e为实际边数
　　VHeadNode adjlist[MAXVEX];	//单链表头结点数组
} AdjGraph;				//图的邻接表类型

• 建立图的邻接表运算算法
  　　先创建邻接表头结点数组，并置所有头结点的firstarc为NULL，遍历邻接矩阵数组A，当A[i][j]≠0且A[i][j]≠∞时，说明有一条从顶点i到顶点j的边，建立一个边结点p，置其adjvex域为j，其weight域为A[i][j]，将p结点插入到顶点i的单链表头部

void CreateGraph(AdjGraph *&G,int A[][MAXVEX],int n,int e)
{      int i,j;
　　ArcNode *p;
　　G=(AdjGraph *)malloc(sizeof(AdjGraph));
　　G->n=n; G->e=e;
　　for (i=0;i<G->n;i++)		//邻接表中所有头结点的指针域置空
	G->adjlist[i].firstarc=NULL;
　　for (i=0;i<G->n;i++)		//检查A中每个元素
	for (j=G->n-1;j>=0;j--)
	　　if (A[i][j]>0 && A[i][j]<INF)		//存在一条边
	　　{    p=(ArcNode *)malloc(sizeof(ArcNode));    //创建一个结点*p
		p->adjvex=j;
		p->weight=A[i][j];
		p->nextarc=G->adjlist[i].firstarc;  //采用头插法插入*p
		G->adjlist[i].firstarc=p;
	　　}
}

• 销毁图运算算法
  　　邻接表的头结点和边结点都是采用malloc函数分配的，在不再需要时应用free函数释放所有分配的空间。其基本思想是，通过adjlist数组遍历每个单链表，释放所有的边结点，最后释放adjlist数组的空间。

void DestroyGraph(AdjGraph *&G)	//销毁图
{      int i;  ArcNode *pre,*p;
　　for (i=0;i<G->n;i++)		//遍历所有的头结点
　　{	pre=G->adjlist[i].firstarc;
	if (pre!=NULL)
	{      p=pre->nextarc;
	　　while (p!=NULL)	//释放adjlist[i]的所有边结点空间
	　　{	free(pre);
		pre=p; p=p->nextarc;
	　　}
	　　free(pre);
	}
　　}
　　free(G);			//释放G所指的头结点数组的内存空间
}

• 输出图运算算法

void DispGraph(AdjGraph *G)	//输出图的邻接表
{      ArcNode *p;
　　int i;
　　for (i=0;i<G->n;i++)		//遍历所有的头结点
　　{	printf("  [%2d]",i);
	p=G->adjlist[i].firstarc;	//p指向第一个邻接点	
	if (p!=NULL)
	　　printf(" →");
	while (p!=NULL)
	{      printf(" %d(%d)",p->adjvex,p->weight);
	　　p=p->nextarc;	//p移向下一个邻接点
	}
	printf("\n");
　　}
}

• 添加一个顶点运算算法

void AddaVex(AdjGraph *&G)
{
　　G->n++;
}

• 插入边运算算法，在图G中添加一条从顶点u到v、权值为w的边。

int InsertEdge1(AdjGraph *&G,int u,int v,int w)	//在无向图中插入一条边
{　  ArcNode *p,*q;
　　if (u<0 || u>=G->n || v<0 || v>=G->n)
	return 0;		//顶点编号错误返回0
　　p=(ArcNode *)malloc(sizeof(ArcNode));
　　p->adjvex=v;
　　p->weight=w;		//建立一个边结点*p
　　p->nextarc=G->adjlist[u].firstarc;	//将*p插入到顶点u的单链表开头
　　G->adjlist[u].firstarc=p;
　　q=(ArcNode *)malloc(sizeof(ArcNode));
　　q->adjvex=u;
　　q->weight=w;		//建立一个边结点*q
　　q->nextarc=G->adjlist[v].firstarc;	//将*q插入到顶点v的单链表开头
　　G->adjlist[v].firstarc=q;
　　G->e++;				//边数增1
　　return 1;
}
int InsertEdge2(AdjGraph *&G,int u,int v,int w)	//在有向图中插入一条边
{      ArcNode *p;
　　if (u<0 || u>=G->n || v<0 || v>=G->n)
	return 0;			//顶点编号错误返回0
　　p=(ArcNode *)malloc(sizeof(ArcNode));
　　p->adjvex=v;
　　p->weight=w;			//建立一个边结点*p
　　p->nextarc=G->adjlist[u].firstarc;	//将*p插入到顶点u的单链表开头
　　G->adjlist[u].firstarc=p;
　　G->e++;				//边数增1
　　return 1;
}

• 求顶点度运算算法

int Degree1(AdjGraph *G,int v)	//求无向图G中顶点v的度
{      int d=0;
　　ArcNode *p;
　　if (v<0 || v>=G->n)
	return -1;		//顶点编号错误返回-1
　　p=G->adjlist[v].firstarc;
　　while (p!=NULL)		//统计v顶点的单链表中边结点个数即度
　　{	d++;
	p=p->nextarc;
　　}
　　return d;
}
int Degree2(AdjGraph *G,int v)	//求有向图G中顶点v的度
{      int i,d1=0,d2=0,d; ArcNode *p;
       if (v<0 || v>=G->n)
　	return -1;		//顶点编号错误返回-1
　　p=G->adjlist[v].firstarc;
　　while (p!=NULL)	//统计v顶点的单链表中边结点个数即出度
　　{	d1++;
	p=p->nextarc;
　　}
　　for (i=0;i<G->n;i++)	//统计边结点中adjvex为v的个数即入度
　　{	p=G->adjlist[i].firstarc;
	while (p!=NULL)
	{      if (p->adjvex==v) d2++;
	　　p=p->nextarc;
	}
　　}
　　d=d1+d2;
　　return d;
}

• 邻接表与邻接矩阵的异同
  联系：邻接表中每个链表对应于邻接矩阵中的一行，链表中结点个数等于一行中非零元素的个数。
  区别：
  对于任一确定的无向图，邻接矩阵是唯一的（行列号与顶点编号一致），但邻接表不唯一（链接次序与顶点编号无关）。
  邻接矩阵的空间复杂度为O(n2),而邻接表的空间复杂度为O(n+e)。
  用途：邻接矩阵多用于稠密图的存储(e接近n(n-1)/2)；而邻接表多用于稀疏图的存储(e<<n2)

代码技巧

• vector：变长数组ADJ[N].
• 其中N为顶点个数，每一个ADJ[i]都是一个变长数组vector，使得存储空间只与图的边数有关
• 若邻接表只存放每条边的终点编号，则

vector<int>ADJ[N];

• 若想添加一条从i号顶点到j号顶点的有向边

ADJ[i].push_back(j);

• 若需要同时存放边的终点编号和边权

struct Node{
	int v;//边的终点编号
	int w;//边权
}

• 这样vector邻接表中的元素类型就是Node型。

vector<Node>ADJ[N];

• 若想添加一条从i号顶点到j号顶点的有向边，且边权为w。

Node temp;
temp.v=j;
temp.w=w;
ADJ[i].push_back(temp);

//使用构造函数 不需要定义临时变量
struct Node{
	int v,w;
	Node(int _v,int_w):v(_v),w(_w){}
}

十字链表

• 结点结构
  顶点结点：date，firstin，firstout
  边结点：tailvex，headvex，hlink，tlink
  临接多重表
• 结点结构
  顶点结点：date，firstdge
  边结点：mark，ivex，ilink，jvex，jlink，info

遍历

• 从图的任意指定顶点出发，依照某种规则去访问图中所有顶点，且每个顶点仅被访问一次，这一过程叫做图的遍历。

深度优先遍历（DFS）

• 类似于树的先根遍历 递归
• 方法
  访问指定的起始顶点；
  若当前访问的顶点的邻接顶点有未被访问的，则任选一个访问之；反之，退回到最近访问过的顶点；直到与起始顶点相通的全部顶点都访问完毕；
  若此时图中尚有顶点未被访问，则再选其中一个顶点作为起始顶点并访问之，转 2； 反之，遍历结束。

const int MAXV=1000;
const int INF=1000000000;
//邻接矩阵版
int n,g[MAXV][MAXV];
int vis[MAX]={0};

void DSF(int u,int depth){
	vis[u]=1;
	for(int v=0;v<n;v++）{
		if(vis[v]==0&&g[u][v]!=INF){
			DSF(v,depth+1);
		}
	}
}
void DSFTrave(){
	for(int u=0;u<n;u++){
		if(vis[u]==0){
			DSF(u,1);
		}
	}
}
//邻接表版
vector<int>ADJ[MAXV];
vis[N]={0};
void DSF(int u,int depth){
	vis[u]=1;
	for(int i=0;i<ADJ[u].size();i++){
		int v=ADJ[u][i];
		if(vis[v]==0){
			DFS(v,depth+1);
		}
	}
}
void DSFTrave(){
	for(int u=0;u<n;u++){
		if(vis[u]==0){
			DSF(u,1);
		}
	}
}

广度优先遍历BSF

• 从图的某一结点出发，首先依次访问该结点的所有邻 接顶点 Vi1, Vi2, …, Vin 再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点，重复此过程，直至所有顶点均被访问为止。
• 队列

const int MAXV=1000;
const int INF=10000000;
//邻接矩阵版
int g[MAXV][MAXV];
int vis[MAXV]={0};
void BSF(int u){
	queue<int>q;
	q.push(u);
	vis[u]=1;
	while(!q.empty){
		int u=q.front();
		q.pop();
		for(int v=0;v<n;v++){
			if(vis[v]==0&&g[u][v]!=INF){
				q.push(v);
				vis[v]=1;
			}
		}
	}
}
void BSFTrave(int u){
	for(int u=0;u<n;u++){
		if(vis[u]==0){
			BSF(u);
		}
	} 
}
//邻接表版1
vector<int>g[MAXV];
int n;
int vis[MAXV];
void BSF(int u){
	queue<int>q;
	q.push(u);
	vis[u]=1;
	while(!q.empty){
		u=q.front();
		q.pop();
		for(int i=0;i<g[u].size(),i++){
			int v=g[u][i];
			if(vis[v]==0){
				q.push(v);
				vis[v]=1;
			}
		}
	}
}
void BSFTrave(int u){
	for(int u=0;u<n;u++){
		if(vis[u]==0){
			BSF(u);
		}
	} 
}
//邻接表版2(带上层号）
struct Node{
	int v;//边的终点编号
	int layer;
};
vector<Node>g[MAXV];
int n;
int vis[MAXV];
void BSF(int u){
	queue<Node>q;
	Node Start;
	start.v=u;
	start.layer=0;
	q.push(start);
	vis[start.v]=1;
	while(!q.empty){
		Node topNode=q.front();
		q.pop();
		for(int i=0;i<g[u].size(),i++){
			Node next=g[u][i];
			next.layer=topNode.layer+1;
			if(vis[v]==0){
				q.push(next);
				vis[next.v]=1;
			}
		}
	}
}

最短路径

• 有向网中 A 点（源点）到达 B 点（终点）的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

单源最短路径

从某个源点到其余各顶点的最短路径

迪杰斯特拉（Dijkstra）算法

• 算法思想
  把 V 分成两组：
  S：已求出最短路径的顶点的集合。
  V - S = T：尚未确定最短路径的顶点集合。
  将 T 中顶点按最短路径递增的次序加入到 S 中，
  保证：从源点 v0 到 S 中各顶点的最短路径长度都不大于从 v0 到 T 中任何顶点的最短路径长度。
  每个顶点对应一个距离值：
  S 中顶点：从 v0 到此顶点的最短路径长度。
  T 中顶点：从 v0 到此顶点的只包括S 中顶点作中间顶点的最短路径长度。

const int MAXV=1000;
const int INF=100000000;
//邻接矩阵版
int g[MAXV][MAXV];
int vis[MAXV]={0};
int d[MAXV];
int n;
vector<int>pre[MAXV];
void Dijkstra(int s){
	fill(d,d+MAXV,INF);
	d[s]=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(d[j]<MIN){
				u=j
				MIN=d[j];
			}
		}
		if(u==-1)return;
		vis[u]=1;
		for(int v=0;v<n;v++){
			if(vis[v]==0&&g[u][v]!=INF){
				if(d[u]+g[u][v]<d[v]){
					d[v]=d[u]+g[u][v];
					pre[v].clear();
					pre[v].push_back(u);
				}
				if(d[u]+g[u][v]==d[v]){
					pre[v].push_back(u);
				}
			}
		}
	}
}
//邻接表版
struct Node{
	int v;//边的终点编号
	int dis;
};
vector<Node>g[MAXV];
int vis[MAXV]={0};
int d[MAXV];
int n;
vector<int>pre[MAXV];
void Dijkstra(int s){
	fill(d,d+MAXV,INF);
	d[s]=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(d[j]<MIN){
				u=j
				MIN=d[j];
			}
		}
		if(u==-1)return;
		vis[u]=1;
		//只有这与邻接矩阵不同
		for(int j=0;j<n;j++){
			int v=[u][j].v;
			if(vis[v]==0){//
				if(d[u]+g[u][v].dis<d[v]){
					d[v]=d[u]+g[u][v].dis;
					pre[v].clear();
					pre[v].push_back(u);
				}
				if(d[u]+g[u][v].dis==d[v]){
					pre[v].push_back(u);
				}
			}
		}
	}
}
//若最短路径只有一条 则创建数组pre[MAXV],初始化，pre[v]=u

• 给每条边再增加一个边权cost 路径长度相同时 找花费最少的

//初始化时只有c[s]=0,其他均为INF
for(int v=0;v<n;v++){
	if(vis[v]==0&&g[u][v]!=INF){
		if(d[u]+g[u][v]<d[v]){
			d[v]=d[u]+g[u][v];
			c[v]=c[u]+cost[u][v];
		}
		if(d[u]+g[u][v]==d[v]&&c[v]>c[u]+cost[u][v]){
			c[v]=c[u]+cost[u][v];
		}
	}
}

• 新增加点权 w找点权多的

//初始化时只有w[s]=weight[s],其他均为0
for(int v=0;v<n;v++){
	if(vis[v]==0&&g[u][v]!=INF){
		if(d[u]+g[u][v]<d[v]){
			d[v]=d[u]+g[u][v];
			w[v]=w[u]+weight[u][v];
		}
		if(d[u]+g[u][v]==d[v]&&w[v]<w[u]+weight[u][v]){
			w[v]=w[u]+weight[u][v];
		}
	}
}

• 求最短路径条数

//初始化时只有num[s]=1,其他均为0
for(int v=0;v<n;v++){
	if(vis[v]==0&&g[u][v]!=INF){
		if(d[u]+g[u][v]<d[v]){
			d[v]=d[u]+g[u][v];
			num[v]=num[u];
		}
		if(d[u]+g[u][v]==d[v]){
			num[v]+=num[u];
		}
	}
}

• Dijkstra+DSF

int optvalue;
vector<int>pre[MAXV];
vector<int>path,tempPath;
void DSF(int v){
	if(v==st){//递归边界
		tempPath.push_back(v);
		int value;
		计算路径tempPath上的value值；
		if(value优于optvalue){
			temp=tempPath;
			optvalue=value;
		}
		tempPath.pop_back();
		return;
	}
	tempPath.push_back(v);
	for(int i=0;i<pre[v].size();i++){
		DSF(pre[v][i];
	}
	tempPath.pop_back();
}
//边权之和
int value=0;
for(int i=tempPath.size-1;i>0;i--){
	int id=tempPath[i],idNext=tempPath[i-1];
	value+=v[id][idNext];
}
//点权值和
int value=0;
for(int i=tempPath.size-1;i>0;i--){
	int id=tempPath[i];
	value+=W[id];
}

Bellman-Ford算法

• 求解有负权边的最短路径问题
• 根据环中边权之和的正负，可以将环分为正环、负环、零环。
  若图中有负环，且从原点可以到达，就会影响最短路径的求解。
  若图中的负环无法从原点到达，则最短路径的求解不会受到影响。
  算法思想
  对图中的边进行V-1轮操作，每轮操作都遍历图中所有的边：对每条边u->v，若以u为中介点可以使d[v]更小，即d[u]+length[u->v]<d[v]，就更新d[v].
  此时，若图中没有源点可达的负环，数组d中的所有值都达到最优。
  再对所有的边进行一轮操作，若存在d[u]+length[u->v]<d[v]，返回false。

struct Node{
	int v,dis;
};
vector<Node>ADJ[MAXV];
int n;
int d[MAXV];
bool Bellman(int s){
	fill(d,d+MAXV,INF);
	d[s]=0;
	for(int i=0;i<n-1;i++){
		for(int u=0;u<n;u++){
			for(int j=0;j<ADJ[u].size();j++){
				int v=ADJ[u][j].v;
				int dis=ADJ[u][j].dis;
				if(d[u]+dis<d[v]){
					d[v]=d[u]+dis;
				}
			}
		}
	}
	for(int u=0;u<n;u++){
		for(int j=0;j<ADJ[u].size();j++){
			int v=ADJ[u][j].v;
			int dis=ADJ[u][j].dis;
			if(d[u]+dis<d[v]){
				return false;
			}
		}
	}
	return true;
}

• 使用Bellman求解最短路径条数时

set<int>pre[MAXV];
if(d[u]+dis<d[v]){
	num[v]=num[u];
}
if(d[u]+dis==d[v]){
	num[v]==0;
	set<int>::iterator it;
	for(it=pre[v].begin();it!=per[v].end();it++){
		num[v]+=num[*it];
	}
}

对Bellman的优化—SPFA

vector<Node>ADJ[MAXV];
int n,d[MAXV],num[MAXV];//num用来记录顶点入队的次数
int vis[MAXV];
bool SPFA(int s){
	fill(vis,vis+MAXV,0);
	fill(num,num+MAXV,0);
	fill(d,d+MAXV.INF);
	queue<int>q;
	q.push(s);
	vis[s]=1;
	num[s]++;
	dis[s]=0;
	while(!q.empty){
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(j=0;j<ADJ[u].size();j++){
			int v=ADJ[u][j].v;
			int dis=ADJ[u][j].dis;
			if(d[u]+dis<d[v]){
				d[v]=d[u]+dis;
				if(vis[v]==0){
					q.push(v);
					vis[v]=1;
					num[v]++;
					if(num[v]>=n)return false;//有可达负环
				}
			}
		}
	}
	return true;
}

全源最短路径

• 每对顶点间的最短路径

弗洛伊德（Floyd）算法

• 算法思想
  若果存在顶点k，使得以k作为中介时，顶点i和顶点j的当前路径缩短，则使用顶点k作为顶点i和顶点j的中介

void Floyd(){
	for(int k=0;k<n;k++){
		for(i=0;i<n;i++){
			for(j=0;j<n;j++){
				if(dis[i][k]!=INF&&dis[k][j]!=INF&&dis[i][k]+dis[k][j]<dis[i][j]){
					dis[i][j]=dis[i][k]+dis[k][j];
				}
			}
		}
	}
}

最小生成树

• 在给定的无向图G（V,E）中求得一棵树T，使得这棵树拥有图G中的所有顶点，且所有边都是来自图G中的边，并且满足整棵树的边权之和最小。
• 生成树：是一个极小连通子图，它含有图中全部顶点，但只有n-1条边。
• 生成森林：由若干棵生成树组成，含全部顶点，但构成这些树的边是最少的。
• 求生成树的方法—DFS(深度优先搜索)和BFS(广度优先搜索)
• 最小生成树可以不唯一，但组小生成树的边权一定是唯一的。
• 贪心法

普利姆（Prim）算法

• 加点（类似于Dijkstra）
• 适合稠密图

const int MAXV=1000;
const int INF=100000000;
//邻接矩阵版
int g[MAXV][MAXV];
int vis[MAXV]={0};
int d[MAXV];
int n;
vector<int>pre[MAXV];
int Prim(){
	fill(d,d+MAXV,INF);
	d[0]=0;
	int ans=0;//存放最小生成树的边权之和
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(d[j]<MIN&&vis[j]==0){
				u=j;
				MIN=d[j];
			}
		}
		if(u==-1)return-1;
		vis[u]=1;
		ans+=d[u];
		for(int v=0;v<n;v++){
			if(vis[v]==0&&g[u][v]!=INF&&g[u][v]<d[v]){
				d[v]=g[u][v];
			}
		}
	}
	return ans;
}
//邻接表版
struct Node{
	int v;//边的终点编号
	int dis;
};
vector<Node>g[MAXV];
int vis[MAXV]={0};
int d[MAXV];
int n;
int Prim(){
	fill(d,d+MAXV,INF);
	d[s]=0;
	int ans=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(d[j]<MIN&&vis[j]==0){
				u=j
				MIN=d[j];
			}
		}
		if(u==-1)return-1;
		vis[u]=1;
		ans+=d[u];
		//只有这与邻接矩阵不同
		for(int j=0;j<n;j++){
			int v=[u][j].v;
			if(vis[v]==0&&g[u][v].dis<d[v]){//
				d[v]=+g[u][v].dis;
			}
		}
	}
	return ans;
}

克鲁斯卡尔（kruskal）算法

• 加边（并查集）
• 稀疏图

struct edge{
	int u,v;
	int cost;
}E[MAXE];
int father[N];
int findFather(int x){
	int a=x;
	while(x!=father[x]){
		x=father[x];
	}
	while(a!=father[a]){
		int z=a;
		a=father[a];
		father[z]=x;
	}
	return x;
}
bool cmp(edge a,edge b){
	return a.cost<b.cost;
}
int Kruskral(int n,int m){//n为顶点个数，m为边数
	int ans=0,Num_egde=0;
	for(int i=1;i<=n;i++)father[i]=i;
	sort(E,E+MAXE,cmp);
	for(int i=0;i<m;i++){
		int fau=findFather(E[i].u);
		int fav=finfFather(E[i].v);
		if(fau!=fav){
			father[fau]=fav;
			ans+=E[i].cost;
			Num_edge++;
			if(Num_edge==n-1)break;
		}
	}
	if(Num_edge!=n-1)return -1;
	else return ans;
}

拓扑排序（待续）

• 若有一个有向图的任意顶点都无法通过一些有向边回到自身，那么称这个图为有向无环图（DAG）。
• 拓扑排序：将有向无环图G的所有顶点排成一个线性序列
• 算法思想
  定义一个队列q，将所有入度为q的顶点加入队列
  取队首节点输出，然后删去所有从他出发的边，并令这些边到达的顶点的入度-1，若某个顶点的入度减为0，将其加入队列。直到队为空。
  若队列为空时，如果队的节点数目恰好为n，则排序成功，g为有向无环图。否则失败。

vector<int>g[MAXN];
int n,m,inDegree[MAXV];
bool tppologicalSort(){
	int num=0;//记录加入拓扑序列的顶点数
	queue<int>q;
	for(int i=0;i<n;i++){
		if(inDegree[i]==0){
			q.push();
		}
	}
	while(!q.empty){
		int u=q.front();
		q.pop();
		for(int i=0;i<g[u].size();i++){
			int v==g[u][i];
			inDegree[v]--;
			if(inDegree[v]==0){
				q.push(v);
			}
		}
		g[u].clear();
		num++;
	}
	if(num==n)return true;
	else return false;
}

关键路径

• AOV网（顶点活动网）：顶点表示活动，边表示活动间优先关系的有向图。

• AOE网（边活动网）：带权的边表述活动，顶点表示事件的有向图。不允许有回路。
  添加超级源点、超级汇点。

• AOV->AOE
  将AOV网中的每个顶点拆成两个顶点，分别表示活动的起点和终点，两个顶点之间用有向边连接，表示活动，边权给定。

• AOE网中的最长路径被称为关键路径，关键路径上的活动称为关键活动。

• 最长路径：图中的最长简单路径。

• List item

• 关键路径
  事件的最早发生时间可以看成旧活动的最早结束时间。
  事件的最迟发生时间可以看成新活动的最迟开始时间。

//拓扑序列
stack<int>topOrder;
//拓扑排序+ve
vector<Node>g[MAXN];
int n,m,inDegree[MAXV];
bool tppologicalSort(){
	queue<int>q;
	for(int i=0;i<n;i++){
		if(inDegree[i]==0){
			q.push();
		}
	}
	while(!q.empty){
		int u=q.front();
		q.pop();
		topOrder.push(u);
		for(int i=0;i<g[u].size();i++){
			int v==g[u][i];
			inDegree[v]--;
			if(inDegree[v]==0){
				q.push(v);
			}
		}
		if(ve[u]+g[u][v].w>ve[v]){
			ve[v]=ve[u]+g[u][v].w;
		}
	}
	if(topOrder.size()==n)return true;
	else return false;
}
int CriticalPath(){
	fill(ve,ve+n,0);
	if(topologicalSort()==false)return -1;
	fill(vl,vl+n,ve[n-1]);
	while(!topOrder.empty){
		int u=topOrder.top();
		topOrder.pop();
		for(int i=0;i<g[u][i].size();i++){
			int v=g[u][i].v;
			if(vl[v]-g[u][i].weight<vl[u]){
				vl[u]=vl[v]-g[u][i].weight;
			}
		}
	}
	for(int u=0;u<n;u++){
		for(int i=0;i<g[u].size();i++){
			int v=g[u][i].v,w=g[u][i].weight;
			int e=ve[u];
			int l=vl[u]-w;
			if(e==l)printf("%d->%d\n",u,v);
		}
	}
	return ve[n-1];
}