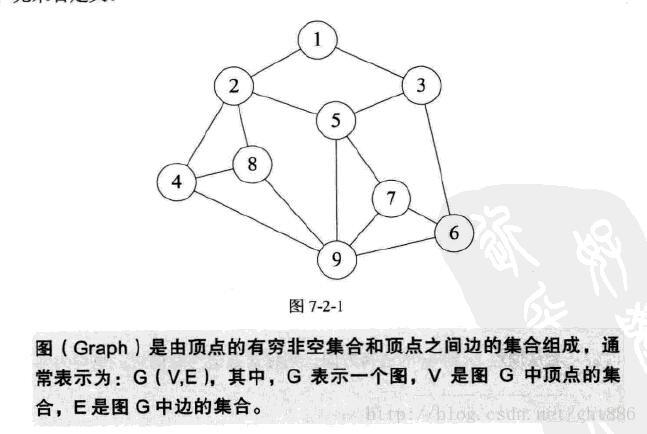
| 图的相关定义: |
- 在图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
- 图按照边的有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。
- 图按照边或弧的多少分稀疏图和稠密图。如果图中的任意两个顶点之间都存在边叫做完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
- 图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度。有向图顶点分为入度和出度。
- 图上的边或弧带有权则称为网。
- 图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环,当中不重复的叫简单路径。若任意两顶点都是连通的,则图就是连通图,有向则称为强连通图。图中有子图,若子图极大连通则就是连通分量,有向的则称为强连通分量。
- 无向图中连通且n个顶点n-1条边称为生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
| 图的遍历 |
图的遍历就是从图中的某个顶点出发,按某种方法对图中的所有顶点访问且仅访问一次。为了保证图中的顶点在遍历过程中仅访问一次,要为每一个顶点设置一个访问标志。通常有两种方法:深度优先搜索(DFS)和广度优先搜索(BFS).这两种算法对有向图与无向图均适用。
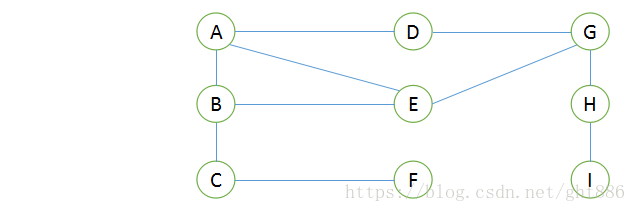
1.深度优先搜索(DFS)
基本步骤:
1.从图中某个顶点v0v0出发,首先访问v0v0;
2.访问结点v0v0的第一个邻接点,以这个邻接点vtvt作为一个新节点,访问vtvt所有邻接点。直到以vtvt出发的所有节点都被访问到,回溯到v0v0的下一个未被访问过的邻接点,以这个邻结点为新节点,重复上述步骤。直到图中所有与v0v0相通的所有节点都被访问到。
3.若此时图中仍有未被访问的结点,则另选图中的一个未被访问的顶点作为起始点。重复深度优先搜索过程,直到图中的所有节点均被访问过。

2.广度优先搜索(BFS)
BFS类似与树的层次遍历,从源顶点s出发,依照层次结构,逐层访问其他结点。即访问到距离顶点s为k的所有节点之后,才会继续访问距离为k+1的其他结点。
基本步骤:
1.从图中某个顶点v0v0出发,首先访问v0v0;
2.依次访问v0v0的各个未被访问的邻接点。
3.依次从上述邻接点出发,访问他们的各个未被访问的邻接点。始终保证一点:如果vivi在vkvk之前被访问,则vivi的邻接点应在vkvk的邻接点之前被访问。重复上述步骤,直到所有顶点都被访问到。
4.如果还有顶点未被访问到,则随机选择一个作为起始点,重复上述过程,直到图中所有顶点都被访问到。
| 最小生成树: |
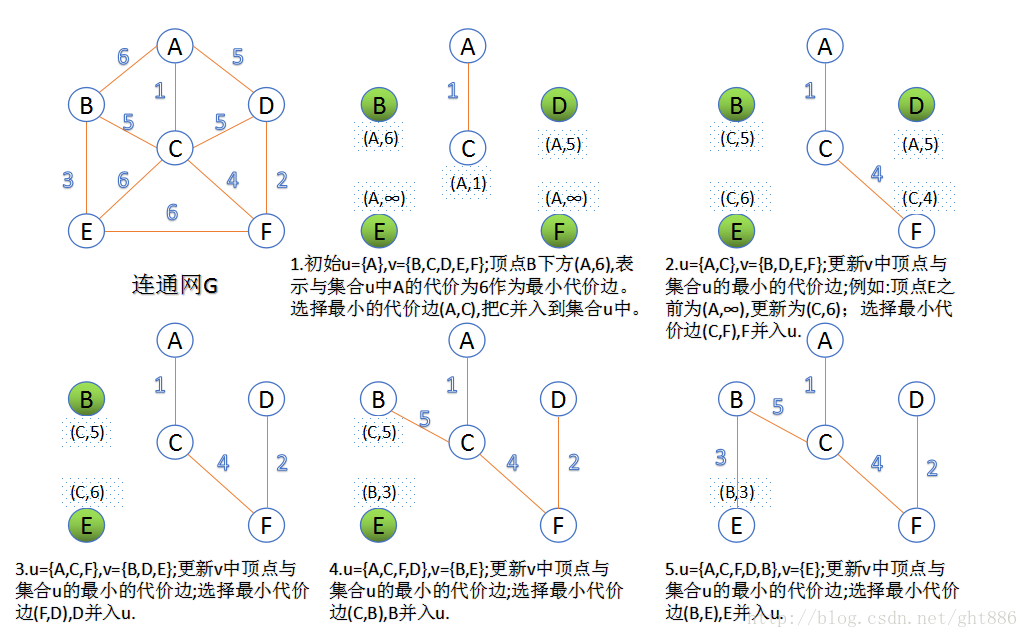
1.普里姆(Prim)算法:
- 此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为VV;初始令集合u={s},v=V−uu={s},v=V−u;
在两个集合u,vu,v能够组成的边中,选择一条代价最小的边(u0,v0)(u0,v0),加入到最小生成树中,并把v0v0并入到集合u中。 - 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
- 由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息。
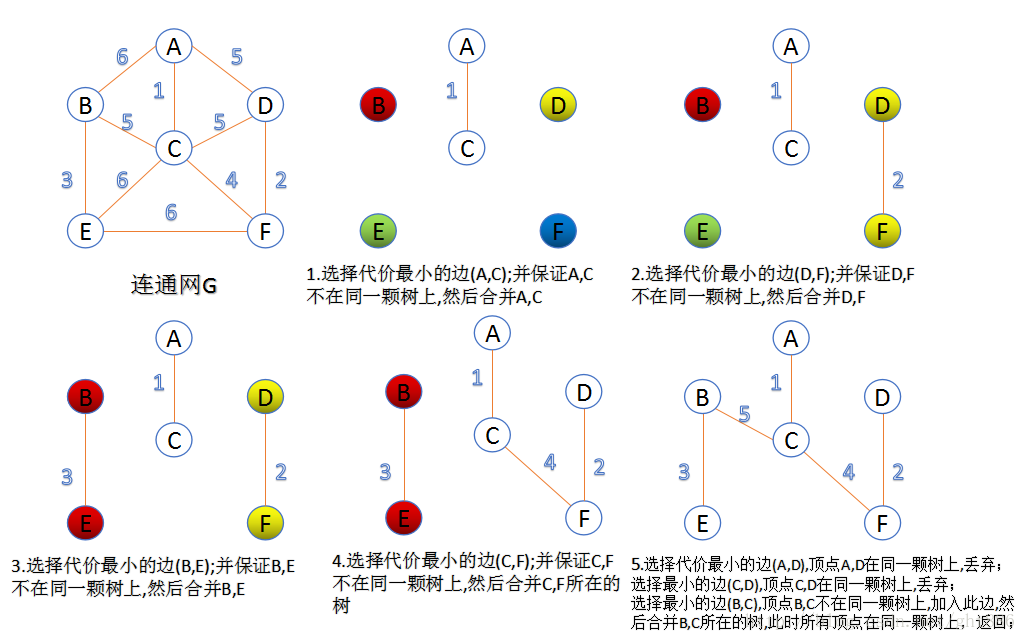
2.克鲁斯卡尔(Kruskal)算法
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
1. 把图中的所有边按代价从小到大排序;
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
| 算法对比 |
普里姆算法更加注重的是结点,点与点之间距离最短的优先;克鲁斯卡尔算法更加注重的是边,将边排序,最小边排在前面,最大边排在后面。