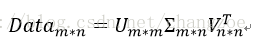机器学习之奇异值分解SVD及应用于协同过滤推荐和LSA潜在语义分析

隐形语义分析LSA

隐形语义分析（LSA）是一种自然语言处理中用到的方法，又称为隐形语义索引 LSI，其通过“矢量语义空间”来提取文档与词中的“概念”，进而分析文档与词之间的关系。LSA的基本假设是，如果两个词多次出现在同一文档中，则这两个词在语义上具有相似性。LSA使用大量的文本上构建一个矩阵，这个矩阵的一行代表一个词，一列代表一个文档，矩阵元素代表该词在该文档中出现的次数，然后再此矩阵上使用奇异值分解（SVD）来保留列信息的情况下减少矩阵行数，之后每两个词语的相似性则可以通过其行向量的cos值（或者归一化之后使用向量点乘）来进行标示，此值越接近于1则说明两个词语越相似，越接近于0则说明越不相似。

词-文档矩阵（Occurences Matrix)

LSA 使用词-文档矩阵来描述一个词语是否在一篇文档中。词-文档矩阵式一个稀疏矩阵，其行代表词语，其列代表文档。一般情况下，词-文档矩阵的元素是该词在文档中的出现次数，也可以是是该词语的tf-idf(term frequency–inverse document frequency)

降维

在构建好词-文档矩阵之后，LSA将对该矩阵进行降维，来找到词-文档矩阵的一个低阶近似。降维的原因有以下几点：

• 原始的词-文档矩阵太大导致计算机无法处理，从此角度来看，降维后的新矩阵式原有矩阵的一个近似。
• 原始的词-文档矩阵中有噪音，从此角度来看，降维后的新矩阵式原矩阵的一个去噪矩阵。
• 原始的词-文档矩阵过于稀疏。原始的词-文档矩阵精确的反映了每个词是否“出现”于某篇文档的情况，然而我们往往对某篇文档“相关”的所有词更感兴趣，因此我们需要发掘一个词的各种同义词的情况。

由于降维要用到SVD，下边介绍矩阵分解SVD

---

---

SVD

奇异值分解原理

矩阵只有对角元素，其余元素为0 ，将这些对角元素从大到小排列，我们称为奇异值。
一般PCA用的是矩阵的特征值，奇异值其实就是Data * Data^T 的特征根
：原理
http://blog.csdn.net/zhongkejingwang/article/details/43053513

python实现
基于numpy包的linalg就可实现

from numpy import *  
'''
生成数据
'''  
def loadExData():  
    return[[0, 0, 0, 2, 2],  
           [0, 0, 0, 3, 3],  
           [0, 0, 0, 1, 1],  
           [1, 1, 1, 0, 0],  
           [2, 2, 2, 0, 0],  
           [5, 5, 5, 0, 0],  
           [1, 1, 1, 0, 0]] 

data = loadExData()
U,Sigma,VT=linalg.svd(data)
Sigma
array([  9.64365076e+00,   5.29150262e+00,   6.51609210e-16,
         2.14818942e-16,   5.18511491e-17])

其中S向量只存储了对角元素的成分，可以大大节省存储空间。接下来我们就需要保留部分奇异值，，一个典型的方法就是奇异值的平方和的累加总值为90%为止。另一种方法就是，有千万的奇异值时，只保留2000或3000个。

应用：

基于协同过滤的推荐引擎

基于用户与其他用户的数据进行对比来实现精确推荐
比如说对于用户没有看过的电影，我们只需要计算与用户看过的电影中的高评分电影的相似度，然后推荐相似度高的电影即可

相似度计算

• 1/(1+距离)
• 皮尔逊相关系数 numpy 用corrcoef()来实现，由于皮尔逊系数是由-1到1，考虑归一化，采用0.5+0.5*corrcoef() 转化为0到1
• 余弦相似度 linalg.norm（）计算范数
  这篇博客介绍的很详细有趣
  http://blog.csdn.net/yixianfeng41/article/details/61917158

def ecludSim(inA,inB):  
    return 1.0/(1.0 + la.norm(inA - inB))  #计算向量的第二范式,相当于直接计算了欧式距离  

def pearsSim(inA,inB):  
    if len(inA) < 3 : return 1.0  
    return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1] #corrcoef直接计算皮尔逊相关系数  

def cosSim(inA,inB):  
    num = float(inA.T*inB)  
    denom = la.norm(inA)*la.norm(inB)  
    return 0.5+0.5*(num/denom)  #计算余弦相似度 

注意，计算相似度后，最好把数据归一化，一般归一化到0-1的范围。计算相似度中我们一般考虑使用基于物品的相似度的分析。原因是由实际考虑的。设想你有一个商店，商品种类可能不太会变动，但是用户不断进进出出，那么计算那个方便呢！ 对，由于物品的稳定性更高，计算量小，那么就基于物品的推荐即可。

推荐引擎的评价
常用RMSE

推荐未评级的
（1）收集数据！
（2）建立用户评价矩阵
（3）针对特定用户，找到其没有评价的物品，计算其评分
（4）将预测的物品评分从大到小排序，然后推荐给用户。

def standEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0: continue
        overLap = nonzero(logical_and(dataMat[:,item].A>0, \ #.A将矩阵转化成array
                                      dataMat[:,j].A>0))[0]  #给出两个物品中已经被评分的元素
        if len(overLap) == 0: similarity = 0
        else: similarity = simMeas(dataMat[overLap,item], \
                                   dataMat[overLap,j])
        print('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    unratedItems = nonzero(dataMat[user,:].A==0)[1]#find unrated items 
    if len(unratedItems) == 0: return 'you rated everything'
    itemScores = []
    for item in unratedItems:
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N] #对列表进行从大到小逆序排列并返回前N个值

尝试推荐

data = loadExData()

mymat=mat(data)

recommend(mymat,2)

>>>[(2, 2.5), (1, 2.0243290220056256)]

这表明用户2对物品2（矩阵第三行）的预测评分是2.5，物品1是2.05

利用SVD提高推荐的效果

#引入更稀疏矩阵
def loadExData2():
    return[[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
           [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
           [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
           [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
           [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
           [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
           [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
           [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
           [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
           [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
           [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]

利用SVD可以将上诉11维矩阵简化为3维

def svdEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    U,Sigma,VT = la.svd(dataMat)
    Sig4 = mat(eye(4)*Sigma[:4]) #arrange Sig4 into a diagonal matrix
    xformedItems = dataMat.T * U[:,:4] * Sig4.I  #create transformed items
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j==item: continue
        similarity = simMeas(xformedItems[item,:].T,\
                             xformedItems[j,:].T)
        print('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

mymat=loadExData2()
mtmat=mat(mymat)
recommend(mymat,1,estMethod=svdEst)

[(2, 3.4177569186592378), (1, 3.3307171545585641)]

完整代码：

# -*- coding: utf-8 -*-
"""
Created on Fri Dec 22 15:22:36 2017

@author: elenawang
"""

from numpy import *
from numpy import linalg as la

def loadExData():
    return[[0, 0, 0, 2, 2],
           [0, 0, 0, 3, 3],
           [0, 0, 0, 1, 1],
           [1, 1, 1, 0, 0],
           [2, 2, 2, 0, 0],
           [5, 5, 5, 0, 0],
           [1, 1, 1, 0, 0]]

def loadExData2():
    return[[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
           [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
           [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
           [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
           [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
           [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
           [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
           [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
           [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
           [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
           [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]

def ecludSim(inA,inB):
    return 1.0/(1.0 + la.norm(inA - inB))

def pearsSim(inA,inB):
    if len(inA) < 3 : return 1.0
    return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]

def cosSim(inA,inB):
    num = float(inA.T*inB)
    denom = la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)

def standEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0: continue
        overLap = nonzero(logical_and(dataMat[:,item].A>0, \
                                      dataMat[:,j].A>0))[0]
        if len(overLap) == 0: similarity = 0
        else: similarity = simMeas(dataMat[overLap,item], \
                                   dataMat[overLap,j])
        print('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

def svdEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    U,Sigma,VT = la.svd(dataMat)
    Sig4 = mat(eye(4)*Sigma[:4]) #arrange Sig4 into a diagonal matrix
    xformedItems = dataMat.T * U[:,:4] * Sig4.I  #create transformed items
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j==item: continue
        similarity = simMeas(xformedItems[item,:].T,\
                             xformedItems[j,:].T)
        print('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    unratedItems = nonzero(dataMat[user,:].A==0)[1]#find unrated items 
    if len(unratedItems) == 0: return 'you rated everything'
    itemScores = []
    for item in unratedItems:
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]

---

---

LSA降维

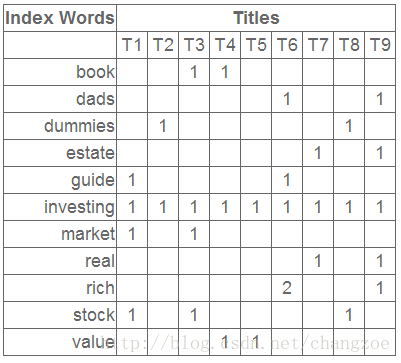
假设X是词-文档矩阵，其元素（i,j）代表词语i在文档j中的出现次数，则X矩阵看上去是如下的样子：

$$\begin{matrix} & \textbf{d}_j \\ & \downarrow \\\textbf{t}_i^T \rightarrow &\begin{bmatrix} x_{1,1} & \dots & x_{1,n} \\\vdots & \ddots & \vdots \\x_{m,1} & \dots & x_{m,n} \\\end{bmatrix}\end{matrix}$$
可以看到，每一行代表一个词的向量，该向量描述了该词和所有文档的关系。

=

$$\begin{bmatrix} x_{i,1} & \dots & x_{i,n} \end{bmatrix}$$
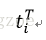
相似的，一列代表一个文档向量，该向量描述了该文档与所有词的关系。

=

$$\begin{bmatrix} x_{1,j} \\ \vdots \\ x_{m,j} \end{bmatrix}$$
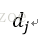
词向量 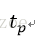的点乘可以表示这两个单词在文档集合中的相似性。矩阵X X^T 包含所有词向量点乘的结果，元素（i,p）和元素（p,i）具有相同的值，代表词p和词i的相似度。类似的，矩阵X^T X包含所有文档向量点乘的结果，也就包含了所有文档那个的相似度。

现在对矩阵X进行奇异值分解（SVD），即：

$$\begin{matrix}X = U \Sigma V^T\end{matrix}$$

因此，词与文本的相关性矩阵可以表示为：

$$\begin{matrix}X X^T &=& (U \Sigma V^T) (U \Sigma V^T)^T = (U \Sigma V^T) (V^{T^T} \Sigma^T U^T) = U \Sigma V^T V \Sigma^T U^T = U \Sigma \Sigma^T U^T \\X^T X &=& (U \Sigma V^T)^T (U \Sigma V^T) = (V^{T^T} \Sigma^T U^T) (U \Sigma V^T) = V \Sigma^T U^T U \Sigma V^T = V \Sigma^T \Sigma V^T\end{matrix}$$

因为 \Sigma \Sigma^T与\Sigma^T \Sigma是对角矩阵，因此U 肯定是由X X^T的特征向量组成的矩阵，同理V是X^T X特征向量组成的矩阵。这些特征向量对应的特征值即为\Sigma \Sigma^T中的元素。综上所述，这个分解看起来是如下的样子：

$$\begin{matrix} & X & & & U & & \Sigma & & V^T \\ & (\textbf{d}_j) & & & & & & & (\hat{\textbf{d}}_j) \\ & \downarrow & & & & & & & \downarrow \\(\textbf{t}_i^T) \rightarrow &\begin{bmatrix} x_{1,1} & \dots & x_{1,n} \\\\\vdots & \ddots & \vdots \\\\x_{m,1} & \dots & x_{m,n} \\\end{bmatrix}&=&(\hat{\textbf{t}}_i^T) \rightarrow&\begin{bmatrix} \begin{bmatrix} \, \\ \, \\ \textbf{u}_1 \\ \, \\ \,\end{bmatrix} \dots\begin{bmatrix} \, \\ \, \\ \textbf{u}_l \\ \, \\ \, \end{bmatrix}\end{bmatrix}&\cdot&\begin{bmatrix} \sigma_1 & \dots & 0 \\\vdots & \ddots & \vdots \\0 & \dots & \sigma_l \\\end{bmatrix}&\cdot&\begin{bmatrix} \begin{bmatrix} & & \textbf{v}_1 & & \end{bmatrix} \\\vdots \\\begin{bmatrix} & & \textbf{v}_l & & \end{bmatrix}\end{bmatrix}\end{matrix}$$

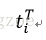
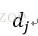
\sigma_1, … \sigma_l 被称作是奇异值，而 u_1, …, u_l 和v_1, …, v_l则叫做左奇异向量和右奇异向量。通过矩阵分解可以看出，原始矩阵中的只与U矩阵的第i行有关,同理，原始矩阵中的只与V^T中的第j列有关.

X_k = U_k \Sigma_k V_k^T

：参考见
http://blog.csdn.net/roger__wong/article/details/41175967

举例：

SVD分解

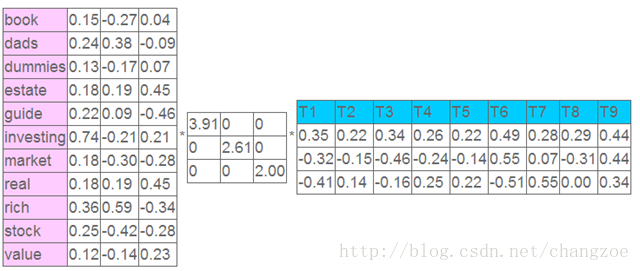
左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程序，数字越大越重要。

继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；
其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。
然后我们反过头来看，我们可以将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上，可以得到

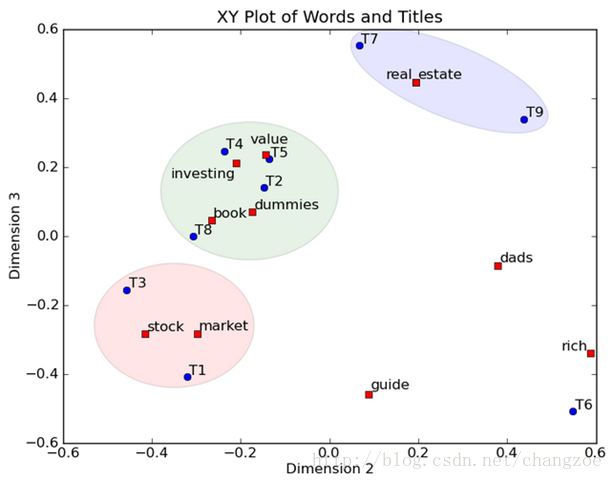
在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

参考：
https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html

http://blog.csdn.net/roger__wong/article/details/41175967