微分几何I

微分几何I——度量、标架

$\quad\quad$在Guass 关于内蕴几何研究的启发下，Riemann认识到作为几何学的基本假设，应当将拓扑性质和空间度量性质区别开来，Riemann、Levi、Civita等人在Riemann度量的发展起到重要作用，Riemann提出为每条曲线提供长度的方法，首先为流形上的切向量指定长度，然后沿着曲线积分来定义曲线长度。在Riemman几何中，Levi-Civita平行移动的概念提出对几何发展起到重要作用。它发展为后续的联络以及向量丛上的联络。
在向量空间V中，考虑函数$\langle \cdot , \cdot\rangle:V\times V \longrightarrow \mathbb{R}$，如果它满足下面两个条件就称为向量V的内积
1. 对称性 ：$\langle u,v\rangle=\langle v,u\rangle，\forall u ,v \in V$
2. 非负性：$\langle u,u\rangle \geq 0,\forall u \in V$，等号成立当且仅当$u=0$

内积的作用就是可以定义长度、角度，有了长度角度应用叉积可以定义面积，它可以把欧式空间长度推广至曲面上，接着我们可以定义RIemann度量。从Riemann 度量从发 定义联络然后是 曲率

定义：设$M$是$m$维光滑流形，$g$是$M$上的二阶协变张量场或者称$(0，2)$型张量场，如果$g$是对称，正定的，称$g$是$M$上的一个Rimann度量。指定了Riemman度量的光滑流形$M$，称为$\bf Riemann流形$，记为$(M,g)$,简记为$M$。

假设正则曲线方程为$r=r(s)$，切向量$d{\bf r}$的长度按内积定义
$$\left|d{\bf r} \right |_g=\sqrt{\langle d{\bf r},d{\bf r}\rangle}$$
有了长度在定义切向量之间的角度：
$$\theta=arccos \left (\frac {\langle d{\bf r},\delta r \rangle}{\left|d{\bf r} \right |_g \cdot \left|\delta{\bf r} \right |_g}\right)$$

图1 曲面参数

设曲面$\Sigma$的参数方程为${\bf r}(u,v)=(x(u,v),y(u,v),z(u,v))$，则坐标$u,v$的切向量为
$$\frac {\partial {\bf r}}{\partial u}=\left (\frac {\partial {x}}{\partial u},\frac {\partial {y}}{\partial u},\frac {\partial {z}}{\partial u}\right) ,\frac {\partial {\bf r}}{\partial v}=\left (\frac {\partial {x}}{\partial v},\frac {\partial {y}}{\partial v},\frac {\partial {z}}{\partial v}\right)$$

如果处处有$\frac{\partial {x}}{\partial v}\times\frac{\partial {x}}{\partial v}\neq0$，则称$\Sigma$为$\bf正则曲面$。

图2 曲面参数

切向量 $${\bf d{\bf r}=\left(\frac {\partial {\bf r}}{\partial u}d{\bf u},\frac {\partial {\bf r}}{\partial v}d{\bf v} \right)=({\bf r}_udu，{\bf r}_vdv})$$
法向量 $${\bf n}= \frac {{\bf r}_u\times{\bf r}_v }{\left |{\bf r}_u\times{\bf r}_v\right|}$$

通过叉积使用长度、角度定义微元面积
$$dA=\left|{\bf r}_ud_u\times {\bf r}_vd_v\right |_g=\left|{\bf r}_u\right| \cdot \left|{\bf r}_u\right| sin(\theta) dudv\\=\sqrt{ {\bf r}_u^2{\bf r}_v^2(1-cos^2(\theta))}dudv\\=\sqrt{ {\bf r}_u^2{\bf r}_v^2-({\bf r}_u \cdot {\bf r}_v)^2}dudv\\=\sqrt{EG-F^2}dudv$$

定义第一基本形式：
$$I=d{\bf r^2}\\={\langle d{\bf r},d{\bf r}\rangle}={\langle( {\bf r}_udu+{\bf r}_vdv), ({\bf r}_udu+{\bf r}_vdv)\rangle} \\={{\bf r}_u \cdot {\bf r}_ududu+2 {\bf r}_u \cdot {\bf r}_v dudv+{\bf r}_v \cdot {\bf r}_vdvdv}\\=Edu^2+2Fdudv+Gdu^2$$
这是一个关于du,dv的二次型，整理成矩阵形式：
$$I= \begin{bmatrix} du & dv \\ \end{bmatrix} \cdot \begin{bmatrix}E &F \\F & G \\ \end{bmatrix} \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}$$

记
$$g=\begin{bmatrix}E &F \\F & G \\ \end{bmatrix}$$
$g$称为度量矩阵。上述计算的微元面积可简化为：
$$dA=\sqrt {det(g)}dudv$$

考虑微分流形M上的两个开集$A,B$，如下图所示，它满足$A$,$B$相交非空，设$A$的局部坐标为$(x,y)$度量为$\rho$；$B$的局部坐标是$(u,v)$，度量为$g$。它们满足坐标变换。$h:(x,y) \rightarrow (u,v)$，相应地微分形式满足变换:
$$\begin{bmatrix} du \\dv\\\end{bmatrix}=\begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}$$

图3 流形M上的坐标变换

在 $A$与 $B$相交的区域，它的基本形式I不依赖于坐标选取，所以有：
$$\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} du & dv\\\end{bmatrix}\cdot g \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}$$
进一步把微分形式变换带入就有：
$$\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} ^T \cdot g \cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix}\cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}$$
所以 $$\rho= \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} ^T \cdot g \cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix}$$
满足上述形式的度量称为在曲面上指定了Riemann 度量。

图4 向量内积

文中开头就介绍了内积定义，那是公理化的定义，现在考虑Riemann度量g定义的内积,假设某点的两个向量为 $d{\bf r},\delta {\bf r}$，则 $d{\bf r}=(dx,dy)$， $\delta{\bf r}=(\delta x,\delta y)$
它们的内积表示为：
$$\langle d{\bf r},\delta {\bf r}\rangle=\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} \delta x \\\delta y\\\end{bmatrix}$$

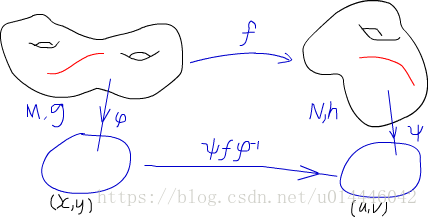
图5 拉回度量

考虑两个Riemann流形 $(M,g)$, $(N,h)$， $\phi,\psi$分别表示两个流形的局部坐标， $M$上的曲线通过 $f$映射到 $N$上，由于在 $N$上有相应的度量，它可以定义 $N$上的长度，这个长度然后拉回到 $M$上，认为是 $M$上的长度。角度也类似。如此就在原 $M$上定义新的度量 $f^*h$，称为拉回度量。
微分形式从M映射到N ： $(dx,dy)\rightarrow(du,dv)$。拉回度量的内积不变
$$\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot f^*h \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} du & dv\\\end{bmatrix}\cdot h \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}$$
可得到 $$f^*h=\left(\frac{\partial (u,v)}{\partial (x,y)}\right)^T\cdot h\cdot \left(\frac{\partial (u,v)}{\partial (x,y)}\right)$$
如果拉回度量与原度量相等 $f^*h=g$,则 $f$是等距变换，若拉回度量与原度量相差一个标量函数 $f^*h=e^{2 \lambda}g$， $\lambda:S\rightarrow\mathbb{R}$是曲面到 $\mathbb{R}$，则 $f$称为共形变换。

$\quad\quad$微分几何的出发点是微积分，一条曲线的切线和微分是同一概念，一条封闭曲线包围的面积相当于对其内部积分。微积分在几何上应用主要是曲线和曲面。首先考虑空间正则曲线$\Gamma$，可以认为它是曲面$\Sigma$上的曲线嵌入在欧式$\mathbb{R^3}$中，曲线参数方程$r=r(s)$,$s$是其弧长参数。对参数方程求导，令${\bf T}(s)=r'(s)$，则${\bf T}(s)$是曲线的切向量(tangent vector)。为了描述曲线的弯曲程度，常常使用曲率的概念，它是切向量对弧长的导数$d{\bf T}(s)/ds$，记为$\kappa(s)$。即：
$${\kappa(s)}=\dfrac{d{\bf T}(s)}{ds}$$
对于单位切向量$\left|{\bf T}(s)\right|=1$，取平方求导可得，${\bf T'}(s){\bf T}(s)$=0，由此可以得出${\bf T'}(s)$与${\bf T}(s)$垂直。定义${\bf T'}(s)$单位向量为${\bf N}(s)$，它表示曲线$\Gamma$的主法向量。有了${\bf T}(s),{\bf N}(s)$这两个向量，可以确定唯一的第2法向量，即：
$${{\bf B}(s)}={\bf T}(s)\times{\bf N}(s)$$
这样${\{r(s),{\bf T}(s),{\bf N}(s),{\bf B}(s)}\}$构成曲线$r(s)$的正交标架。

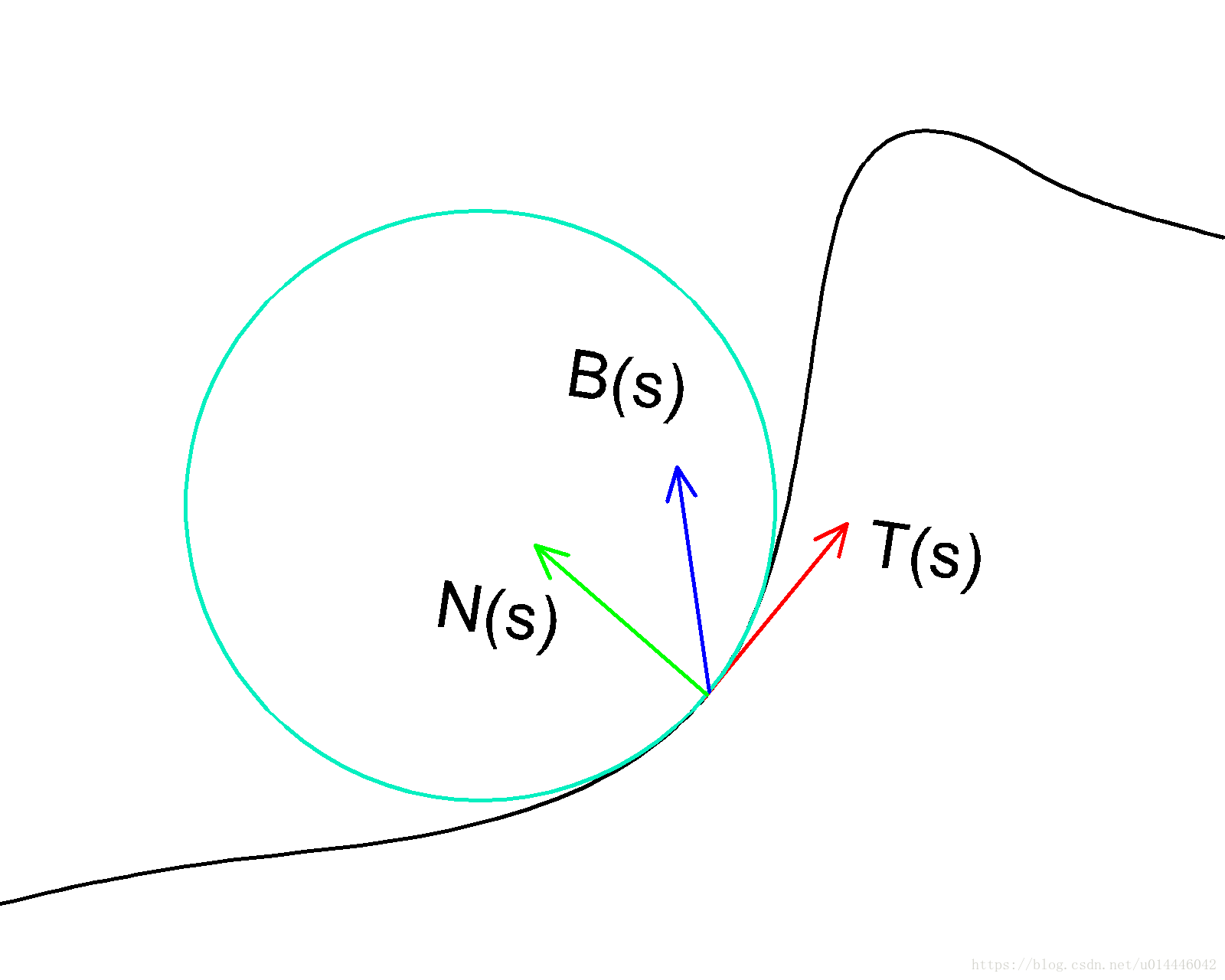
图6 曲线标架

\quad曲线在一点的切线和主法线所张的平面是曲线的密切平面，它的法向量是曲线在p点的次法向量${\bf B}$。前面说过，曲线单位切向量${\bf T}$关于$s$的导数的长度表示曲线的曲率，反映的是曲线的切线方向转动的快慢；类似的是，次法向量关于$s$的导数，反映出曲线的密切平面方向转动的快慢，因而它刻画了曲线偏离平面曲线的程度，即曲线的“挠率”。
由于${\{{\bf T}(s),{\bf N}(s),{\bf B}(s)}\}$分别是单位切向量、单位主法向量、单位次法向量，和前面类似,
${\bf B'} \bot {\bf B}$，此外，${\bf B}(s)={\bf T}(s)\times{\bf N}(s)$，${\bf T'}(s) \parallel {\bf N}(s)$
对${\bf B}(s)$求导可得：
$${\bf B'}(s)={\bf T'}(s)\times{\bf N}(s)+{\bf T}(s)\times{\bf N'}(s)={\bf T}(s)\times{\bf N'}(s)$$
所以${\bf B'} \bot {\bf T}$，${\bf B'}$和${\bf N}$共线，既然共形两者相差一个常数，不妨设 $${\bf B'}=- \tau(s) {\bf N}(s)$$
先前已有 ${\bf N}(s)$是单位向量，上式两边同乘以${\bf N}(s)$可得：
$$\tau(s)=-{\bf B'} (s){\bf N}(s)$$
这里插一个定义：设 ${\bf N}(s)$和 ${\bf B}(s)$分别是曲线C的主法向量和次法向量，其中$s$是曲线的弧长参数，则$\tau(s)=-{\bf B'} (s){\bf N}(s)$称为曲线C的挠率。

有了这些曲率、挠率、标架后我们可以推出曲线运动公式
$$\begin{align} {\bf T}(s) & = r'(s) &\text{切向量} \tag 1\\ {\bf T'}(s) & =\kappa(s){\bf N}(s)& \text{曲率} \tag 2\\ {\bf B'}(s) & = -\tau(s){\bf N}(s) & \text{挠率} \tag 3\\ \end{align}$$

要使用运动公式，上述还缺${\bf N'}(s)$，由右手法则可知：
$${\bf N}(s) ={\bf B}(s)\times{\bf T}(s)$$
两边微分：
$$\begin{align} {\bf N}'(s) & = B'(s) \times T(s)+B(s) \times T'(s) \tag 1\\ & = -\tau(s)N(s)\times T(s)+B(s)\times\kappa(s)N(s) \tag2 \\ & =-\tau(s)\times(-B(s))+\kappa(s)\times(-T(s)) \tag 3\\ & =\tau(s)B(s)-\kappa(s)T(s)\tag4 \end{align}$$

如果整理成矩阵形式：
$$\begin{bmatrix} {\bf T'}(s) \\ {\bf N'}(s)\\ {\bf B'}(s) \\ \end{bmatrix} = \begin{bmatrix}0 & \kappa(s) & 0 \\-\kappa(s) & 0 & \tau(s) \\0 & -\tau(s) & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf T}(s) \\ {\bf N}(s)\\ {\bf B}(s) \\ \end{bmatrix}$$
这个公式称为Frenet公式。

考虑曲面$\Sigma$的参数方程$r(u,v)$，定义$e_1$是曲面S的单位切向量场，在切平面上将$e_1$逆时针旋转$90^\circ$得到$e_2$，$e_1\times e_2$得到$e_3$向量场。$\{r(u,v),e_1(u,v),e_2(u,v),e_3(u,v)\}$构成曲面的局部标架场

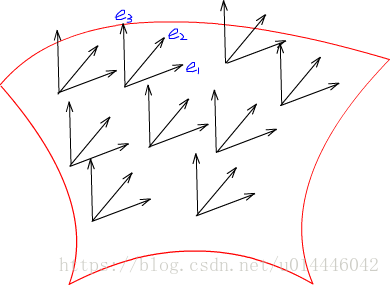
图7 标架场

由微分1形式在切平面上分解
$$d\mathbb{r}=\mathbb{r}_udu+\mathbb{r}_vdv\\= (\langle\mathbb{r}_u,e_1\rangle e_1+\langle\mathbb{r}_u,e_2\rangle) e_2)du\\+(\langle\mathbb{r}_v,e_1\rangle e_1+\langle\mathbb{r}_v,e_2\rangle) e_2)dv\\= (\langle\mathbb{r}_u,e_1\rangle du+\langle\mathbb{r}_v,e_1\rangle) dv)e_1\\+ (\langle\mathbb{r}_u,e_2\rangle du+\langle\mathbb{r}_v,e_2\rangle) dv)e_2\\=\omega_1e_1+\omega_2e_2$$
构成微分形式分解。
同理切向量存在分解： $de_i=\omega_{i1}e_1+\omega_{i2}e_2+\omega_{i3}e_3$
$$\langle e_i,e_j\rangle=\delta^i_j \implies \langle de_i,e_j\rangle+\langle e_i,de_j\rangle=0$ \implies \omega_{ij}+\omega_{ji}=0$$
曲面标架运动方程：
$d\mathbb{r}=\mathbb{r}_udu+\mathbb{r}_vdv=\omega_1e_1+\omega_2e_2$
$$d \begin{bmatrix} {{\bf e}_1} \\ {\bf e}_2\\ {\bf e}_3\\ \end{bmatrix} = \begin{bmatrix}0 & \omega_{12} & \omega_{13} \\-\omega_{12} & 0 &\omega_{23} \\-\omega_{13} & -\omega_{23} & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf e}_1 \\ {\bf e}_2\\ {\bf e}_3 \\ \end{bmatrix}$$
有了微分1-形式的公式，后面的几何计算都可以采用微分形式表示，比较方便。也便于联系上同调等。
基本量用微分形式表示：
1.Riemann 度量： $\langle d{\bf r},d{\bf r}\rangle=\omega_1^2+\omega_2^2$
2.面元: $dA_g=\omega_1 \wedge \omega_2$
3.联络： $\omega_{12}$

联络和平行移动
联络D是为了定义曲面上的切向量的微分而出现的，它与平行移动有关，谈到平行移动首先考虑测地线上的平行移动，测地线是曲面上两点最短线，曲面$S$在点$p$处的切向量$\vec v_p$沿着测地线$\gamma(t)$平行移动满足：1.切向量$\vec v_p$和该点处的测地线的切向量$\gamma'(0)$保持夹角不变；2.切向量$\vec v_p$模长不变；3.$\vec v_p \in T_p^*S$。对于普通曲线取曲线上的分点，在分点之间取测地线，这就是分段测地线，让分点取更细，最后取极限，即可得到平行移动。对于欧式空间的平行移动比较简单，因为测地线是线段，平行移动后向量不变，而对于曲面上的平行移动就比较复杂了。从分析上描述平行移动有利于计算，参考欧式的平行移动，曲面的平行移动可以描述为$D_{\gamma'(t)}\vec v(t))=0$,测地线方程可以描述为$D_{\gamma(t)}\vec v(t)=0$。所以有了联络就可以计算平行移动和测地线了。
定义联络D作用于函数:
$D_{\vec v}f=df(\vec v)$
定义联络D作用于向量:
$D_{\vec v}({fe_1+ge_2})=D_{\vec v}({f})e_1+fD_{\vec v}e_1+D_{\vec v}({g})e_2+gD_{\vec v}e_2$
其中：
$D_{\vec v}({e_1})=\langle De_1, {\vec v}\rangle=\omega_{12}e_2$
$D_{\vec v}({e_2})=\langle De_2, {\vec v}\rangle=-\omega_{12}e_1$

仿照曲面运动方程
$$D_\vec v \begin{bmatrix} {{\bf e}_1} \\ {\bf e}_2\\ {\bf e}_3\\ \end{bmatrix} = \begin{bmatrix}0 & \omega_{12} & 0 \\-\omega_{12} & 0 &0 \\0 & 0 & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf e}_1 \\ {\bf e}_2\\ {\bf e}_3 \\ \end{bmatrix}$$

有了上述公式后续的计算就可以进行了。

参考文献：
1.顾险峰，计算共形几何讲义，高等教育出版社，2008
2.陈省身，微分几何，世界图书出版公司，2006
3.陈维桓，微分几何，北京大学出版社，2006