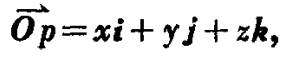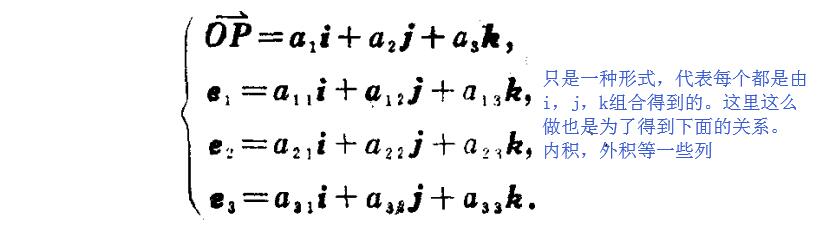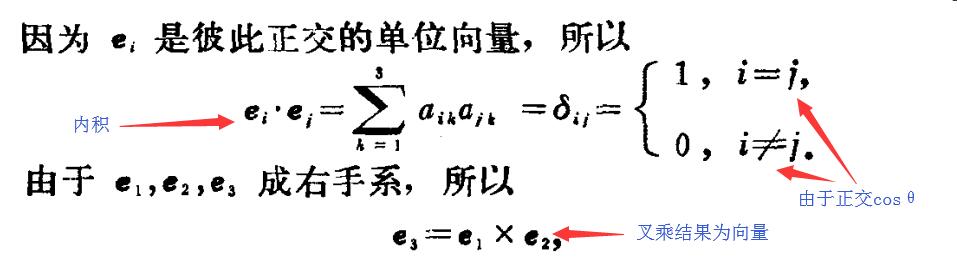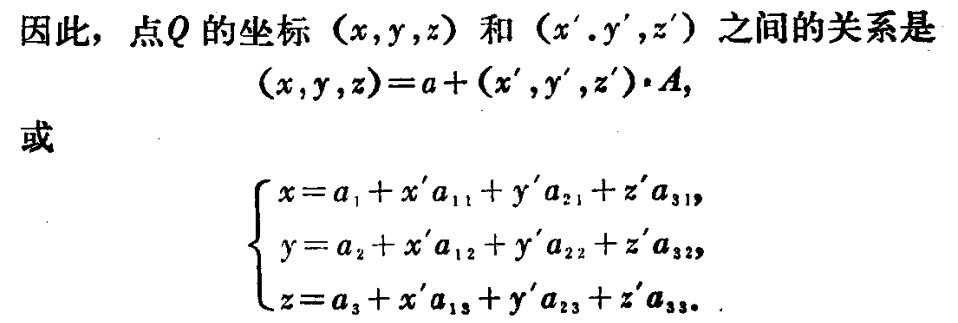1.参数方程
所谓参数方程其实和普通方程类似,都是自变量和因变量的关系。而更为直观地理解是,参数方程是普通方程的延伸,例如:在参数方程中很多时候用到了时间变量‘t’,进而用时间变量‘t’作为变参数去替换我们的x,y。在一元函数中不明显,在二元参数中,我们可以直接用参数‘t’来对原自变量x和y进行替换,至于为什么要替换,需要继续往下看。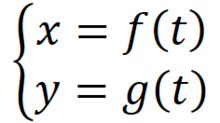
2.坐标和标架
原作解释为建立“形”与“数”之间的桥梁,这种解释非常到位。设想一下如果没有坐标的引入,也就是你从来没有学过什么是坐标,我们所求解的方程我们能看到的只有一堆数,而整个函数的“形状”我们是没有概念的,这个抽象出来的“形状”大概也是在坐标出现以后才诞生的。
3.向量复习
好吧,这里也记录一下,线性代数自己是考过满分的…
向量:大小和方向。
内积:数值,a·b=|a||b|cosθ。(矩阵形式就是对应点相乘再相加,这里对应点的时候涉及到转置,转置就是为了让两个之前都是横向量的变成一个前为横向量后为列向量的乘积。)
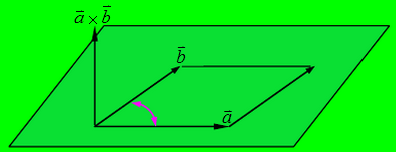
外积:向量,右手定则判断方向。axb,大小为|a||b|sinθ,方向为垂直于a,b所构成的平面。右手定则,四指从a到b,大拇指为外积后向量方向。
很多情况下我们可以看到i,j,k的出现,这些分别是坐标系x,y,z的单位向量,因此在matlab编程时涉及到了x,y,希望不要再为为啥y是for j=1:100而纠结了。
4.标架
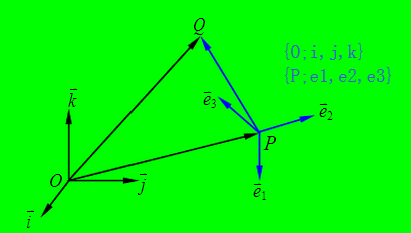
i,j,k分别为x轴,y轴,z轴的正向单位向量,O是坐标原点。笛卡尔坐标(x,y,z)可以用{O;i,j,k}来表示,其中{O;i,j,k}称为三维空间E3右手单位正交标架,简称正交标架。在空间中任取一个点p。我们成向量Op为关于坐标原点O的向径。向径唯一表示为:
这里设了一下一般(不一定与x,y,z重合)的正交标架的集合,{P;e1,e2,e3},位置关系如下
上面还没提到,那个混合积是有正负之分的,看夹角是锐角还是钝角。axb,与c同侧为正,异侧为负。
还有就是可以看出A是行列式为1的正交矩阵,正交的定义式a*a的转置结果为单位矩阵e,也就是a的转置=a的逆。
5.建立两个正交标架的关系
这里写了这么一大堆主要是为了说明确实可以这么转化。
这里最后写出定理:三维空间E3中的刚体运动是把一个正交标架变为另一个正交标架。从E3到自身的变换能保持空间两点的距离不变。也就是对于线性变换只要求变化矩阵A为正交矩阵。等距变化把一个单位正交标架变为另一个单位正交标架,可能会出现左手系变为右手系。
6.仿射标架-由三个不共面的单位向量组成,不一定正交。{P;e1,e2,e3}。