一、树的基本概念
-
树的基本概念
树是n个结点的有限集合T。当n=0时,称为空树;当n>0时,该集合满足如下条件:
①其中必有一个称为根(root)的结点,它没有直接前驱,但有0个或多个直接后继。
②其余n-1个结点可以划分成m(m>=0)互不相交的有限集T1,T2,T3,...Tm,其中Ti又是一棵树,称为根的子树。每棵子树的根节点有且仅有一个直接前驱,但有0个或多个直接后继。
(树是以递归的形式定义的)
下图为一棵树的逻辑结构图示,类似一棵倒长的树:
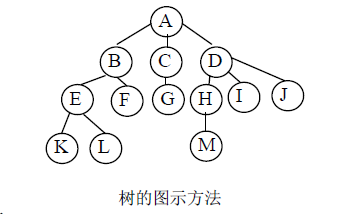
-
树的图解表示法:
-
倒置树结构,(树形表示法),如上图所示。
例如家族关系的表示,A有3个孩子,B、C、D;B有两个孩子E、F ;D有三个孩子H、I、J等。
-
文氏图表示法(嵌套集合表示法),如下图所示。
例如某个国家A,分成3个省B、C、D;B省包括F、E市;E市包括K、L县等。
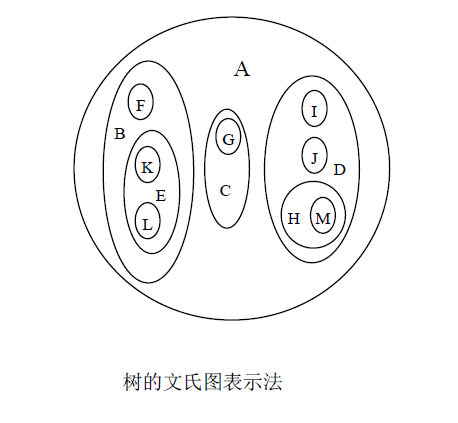
-
广义表形式(嵌套括号表示法),(A(B(E(K,L),F),C(G),D(H(M),I,J)))。
例如一本书A分为B、C、D三章,B章又分为E、F两节,E节又分为K、L两段,等等。
-
凹入表示法,用位置的缩进表示其层次,实际上程序的锯齿形结构就是这种结构。
如图:例如书的目录表的编排格式。

-
-
树相关的术语

- 结点:节点包括一个数据元素及若干指向其他结点的分支信息。
- 结点的度:节点所拥有子树的个数称为节点的度。
- 叶节点:度为0的节点,即无后继的结点,叶结点也称为终端节点。
- 分支节点:度不为0的节点,分支节点又称非终端节点。一棵树中排除叶结点外的所有节点都是分支节点。
- 祖先节点:从根节点到该节点所经分支上的所有节点。
- 子孙节点:以某节点为根节点的子树中所有节点
- 双亲节点:树中某节点有孩子节点,则这个节点称为它孩子节点的双亲节点,双亲节点也成为前驱节点,如:上图中 结点A 是B、C的双亲。
- 孩子节点:树中一个节点的子树的根节点称为该节点的孩子节点,孩子节点也称为后继节点,如上图,结点B、C是A的孩子
- 兄弟节点:具有相同双亲节点的节点称为兄弟节点,如:图中的H、I、J互为兄弟。
- 堂兄弟结点:双亲在同一层,但并非同一个,的结点互为堂兄弟,如:上图中结点E、G、H互为堂兄弟。
- 树的度:树中所有节点的度的最大值成为该树的度。
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,其他节点层次是双亲节点层次加1,以此类推;
- 树的深度(高度):树中所有节点的层次的最大值称为该树的深度。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
- 前辈:层号比该结点小的结点,都称为该节点的前辈。在上图中,结点A、B、C、D都可称为结点E的前辈。
- 后辈:层号比该结点大的结点,都称为该结点的后辈。在上图中,结点K、L、M都可称为结点E的后辈。
-
树的ADT定义
树的抽象数据类型定义:
ADT Tree
{
数据对象D:
一个集合,该集合中的所有元素具有相同的特性。
结构关系R:
若D为空集,则为空树。若D中仅含有一个数据元素,则R为空集,否 则R={H},H是如下的二元关系:① 在D中存在惟一的称为根的数据元素root,它在关系H下没有前驱。
② 除root以外,D中每个结点在关系H下都有且仅有一个前驱。
基本操作:
-
InitTree (Tree): 将Tree初始化为一棵空树。
-
DestoryTree (Tree):销毁树 Tree。
-
CreateTree (Tree):创建树 Tree。
-
TreeEmpty (Tree): 若Tree为空,则返回TRUE,否则返回FALSE。
-
Root (Tree):返回树Tree的根。
-
Parent (Tree,x):树Tree存在,x是Tree中的某个结点。若x为非根结点,则返回它的双亲,否则返回“空”。
-
FirstChild (Tree,x):树Tree存在,x是Tree中的某个结点。若x为非叶子结点, 则返回它的第一个孩子结点,否则返回“空”。
-
NextSibling (Tree,x): 树Tree存在,x是Tree中的某个结点。若x不是其双亲的最后一个孩子结点,则返回x后面的下一个兄弟结点,否则返回“空”。
-
InsertChild (Tree,p,Child):树Tree存在,p指向Tree中某个结点,非空树Child 与Tree不相交。将Child插入Tree中,做p所指向结点的子树。
-
DeleteChild (Tree,p,i):树 Tree 存在,p 指向 Tree 中某个结点1<=i<=d, d 为P所指向结点的度。删除Tree中p所指向结点的第i棵子树。
-
TraverseTree (Tree, Visit ()):树 Tree 存在,Visit ()是对结点进行访问的函数。按照某种次序对树Tree的每个结点调用Visit ()函数访问一次且最多一次。 若Visit ()失败,则操作失败。
}
-