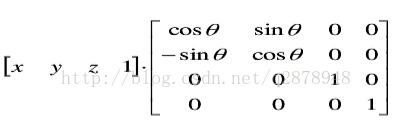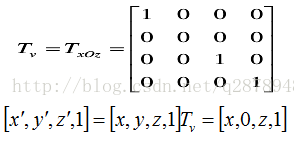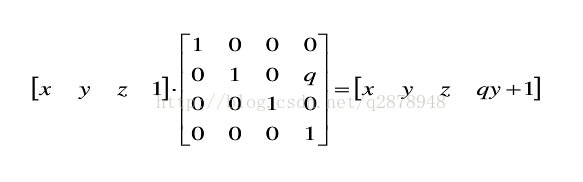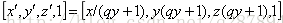本模块内容绝大部分是在慕课上看中国农业大学网客时的笔记,因此算作转载,在此鸣谢赵明、李振波两位老师,感谢他们录制该门课程供大家学习!
在使用计算机处理图像时,我们不可避免对图形的位置、大小、形状等进行改变。如何进行图形变换因而尤为重要。本篇将介绍在计算机中如何进行二维、三维图形的平移、旋转、放缩、投影、错切等变换。
二维三维图形变换
向量、矩阵与图形处理
在讲具体的处理方法之前,首先要介绍一下向量、矩阵等线性代数知识在计算机中的重要地位。
对于计算机来说,用数组储存、操作数据是很方便的,比如跟循环语句非常“合拍”,代码简洁可读性高等等。可见,使用数组在计算机中处理数据是非常方便的。例如,使用矩阵乘法对数据进行处理只需要一个for循环的嵌套即可,简单明了,而无需将每组数据的具体算式写下来,省时省力。
为了方便介绍,下面放几个概念。
向量的仿射组合和凸组合
仿射组合指同维度进行线性组合的向量,其系数之和sum(ai)=1;
凸组合指在仿射组合的前提下,还满足任意系数ai>=0
图形变换的基本原理
在图形变换中,我们需要知道什么是“不变”的,通过“不变”去求变化后的图形。因此,我们应知道:
- 图形边的长度变化,但其连边规则没有变化
- 定点的位置变化,但定点之间的拓扑关系没有变化
由此我们可以得出,图形变化的本质就是按照一定规则改变其顶点坐标,然后重新按照原拓扑关系将定点连接起来。
仿射变换(Affine Transformation 或 Affine Map)
仿射变换是一种从而为到二维的坐标线性变换,它具有两条重要性质,即:
- 平直性,直线变换后仍是直线
- 平行性,平行关系不因变换而改变,且直线上点的顺序关系不变
其变化过程满足:
齐次坐标
齐次坐标的思路是希望用比原数据高一维的变换矩阵来表示顶点的变换方程,比如用三维矩阵表示二维坐标系下的图形变换,用四维矩阵表示三维坐标系中图形的变换等。用具体的数据写出来,以二维坐标下的点为例,就是将点(x,y)写成(x,y,1),然后乘以一个三维矩阵实现具体的变换过程,从而得到变换后的坐标。
齐次坐标经处理之后,再用反投影将它表示回原来的二维/三维坐标系下
我们当然可以通过对每个顶点写出具体的算式,封装成变换函数这样,这样做一则契合计算机处理数据的模式,可以将平移、旋转、放缩、错切等变换写成较为统一的形式;二则可以区分点与向量。在数学中,仍以二维为例,点与向量的表示都为(x,y),如果没有任何标记,区分它们是件麻烦事。但在齐次坐标中,点的表示是(x,y,1),而向量则是(x,y,0),这样的话,根据变换矩阵的不同,像对向量的平移这种操作是不会改变向量值的,因而不会错误地对向量进行坐标点的操作。可能看到这里会有点迷,因为具体的变换矩阵没有给出,但是等明白具体二维空间中如何进行点的平移后,就会晓得到底怎么回事了。
二维图形变换

所有的仿射变换都是通过改变上式中三维矩阵的参数进行的。为了方便,我们将其进行如下分区:
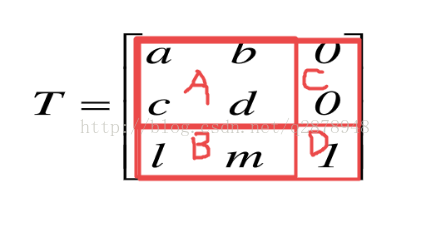
平移变换
B区参数控制平移变换中的平移距离大小。原理如下:
坐标的平移写成表达式,即x*=x+l,y*=y+m,用矩阵表示即为
比例放缩
比例放缩时,我们可以改变A区中的a,d参数而实现。特别地,当x与y坐标放大倍数相同时,我们一般会通过对D区参数的设置,令坐标在反投影时进行整体的比例放缩。S>1,图形缩小,0<S<1放大,S<0时发生关于原点对称的等比变换。原理如下:
坐标的比例放缩表达式:x*=ax,y*=by,表示成矩阵:
反投影时整体放缩的原理:
对称变换
A区参数a,d设置为其相反数可实现关于x轴,y轴的对称变换,而对任意直线对称,我们可以通过适当的平移旋转,将问题转化为关于x,y轴的对称变换。以关于x轴的对称变换原理如下:
旋转变换
旋转变换也是通过设置A区参数实现的。这里的旋转指的是绕原点逆时针旋转,绕任意点的旋转可通过旋转前后平移图形将其转换成绕原点的旋转而实现。
根据三角函数特性,坐标初始位置与原点连线后,与x轴正方向成α角,绕原点逆时针旋转θ角,该变换可以写成如下表达式:
根据极坐标与直角坐标线关系,x,y初值可表示成x=rcosα,y=rsinα,因此将该式代入上面并转换成矩阵表示就是:
错切变换
这个变换可能不是那么耳熟。有时处理图形时,为模拟弹性物体的形变,就要用到它了。错切变换由A区的b,c两个参数控制,下图是错切变换的两个简单实现:
实际上,任何错切变换都可以由若干x方向或y方向的简单错切变换组合而成
以x正方向错切为例,其原理:
x*=x+cy,y*=y,矩阵形式为
对于齐次坐标的一些说明
为什么二维变换不用二维矩阵?
答:我们的旋转、放缩、对称、错切都可以只在A区进行,二维is enough,但是,二维矩阵是无法实现平移变换的,不信你试试就知。因此,为了统一形式,就使用齐次坐标啦
C区是干什么用的?
答:没用。但是,没用仅对二维坐标的齐次坐标来说是没用的。对三维坐标的齐次坐标来说,C区被用来控制透视投影。
复合变换
即是把几个变换矩阵乘在一起,用来表示按照特定步骤进行的一系列变换。需注意的是,特定步骤这四个字,即是说矩阵的乘法不满足交换律,瞎鸡儿乱换会导致奇怪的结果。
坐标系之间的变换是复合变换中的一个例子,当我们需要将原坐标系上的点表示在新坐标系上,需要对坐标系进行变换。该变换可通过平移与旋转,使两个坐标系重合,然后拿出从新坐标系到原坐标系的变换矩阵,就可以通过将原坐标系上的点与这个矩阵相乘得到新坐标系上该点的坐标表示。
多边形的变换
明白了上面的东西,这个问题就变得简单了,只需把原来的(x,y,1)向量改为若干向量组成的矩阵然后乘变换矩阵就行了,其实质还是各顶点的坐标变换。
三维图形变换
三维图形变换的原理与二维类似,均是通过引入齐次坐标对其进行操作。其中的平移,比例变换,对称变换只需将二维坐标齐次坐标的变换矩阵加一维变为4阶矩阵就行;旋转变换看绕哪个坐标轴旋转,就令该坐标所对应的A区参数不变,另外两个坐标对应的A区参数像二维图形变换那样写成三角函数。如绕Z轴旋转,有
因此,下面主要介绍下三维物体的投影变换
平行投影(以三视图为例)
投影变换中最简单的是三视图。其原理是把三维图形的某一坐标置为0,从而使图形落在某坐标平面上(如xOz平面),然后通过旋转和平移将三张投影图放到同一个坐标平面上,就成了三视图。向xOz平面投影的变换矩阵如下
透视投影
透视投影与平行投影的主要区别是其视点在有限远处,用的是中心投影法生成图像,投影的大小与物体到投影中心的距离成反比,这种效果很接近人的视觉系统,因而使物体看上去更接近人眼看到的图像,即更加真实。控制下图的C区参数即可
一点透视
即存在一个透视点(一般让它在坐标轴上),该点处所有平行于该坐标轴的线都交于这一点,这就是一点透视。体现在矩阵中,就是:
q置为非零,p=r=0,然后就可以实现y轴上的一点透视,这里1/q就是那个灭点
齐次化后有
且y趋向无限时,x与z趋向于0,y趋向于1/q
多点透视
类似一点透视,只需控制pqr中非零参数的个数即可。如三点透视,三个灭点分别在1/p,1/q,1/r处
透视投影步骤:
- 将三维物体平移到适当位置
- 透视变换
- 向坐标平面(如xOy)进行正投影变换,方便绘制(二点三点透视需要在平移后旋转一下)
下面是一个单位立方体的一点透视投影变换,视距d=-2.5,位于z轴上。计算步骤如下: