引言
关于支持向量可以参考机器学习入门——支持向量机和李宏毅机器学习——支持向量机。
关于结构化学习的知识建议先阅读下李宏毅机器学习——结构化学习(二)。
本文主要介绍结构化支持向量机的理论知识。
在李宏毅机器学习——结构化学习(二)中我们说,我们要找到合适的框把目标给框出来。今天我们假设无法找到一个这样的框,但是能找到一个近似的,这个问题要怎么解呢。

下文会介绍这个问题的解法。
先看下本文的结构。

可分的情况
我们已经在李宏毅机器学习——结构化学习(二)中讨论了可分(Separable case)的情况。
在这里我们引入了margin。

现在有两份数据,一个用圈圈表示,另一个用星星表示。红色的代表是正确的结果。
所谓可分的意思是存在一个向量 ,如果我们把所有的点都对 做内积,会发现我们能让红点(正确的点)内积结果比同份数据蓝色点内积结果都大一个值,记为 。

比如红色圈圈比所有蓝色圈圈的内积值都大一个
,红色星星也一样。
如果用数学描述就是这样:
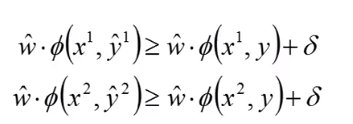
如果是可分的话,我们就可以用下面的算法来找到我们要的参数
。

接下来证明下我们能找到这个向量
。
先看下结论,在可分的情况下,我们最多只要更新
次就能找到
。
是最大 距离的最大值。在同份数据中,把所有的点都代入 可以得到一个距离,任何两点距离了最大的值就是 。
所以这个算法需要迭代的次数与 的空间是无关的,即无论 有多少,只要 确定,迭代次数就确定。
证明如下:
在每次发现错误点的时候就会更新。
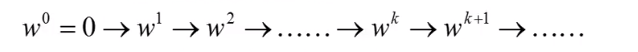
把 的更新过程写出来,我们先看 与 的关系。
我们知道,它们一定有这样的关系:
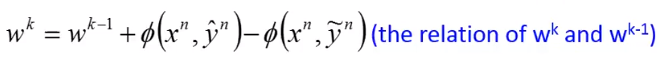
某个正确结果形成的 减去某个错误的 形成的 。
我们考虑的是可分的情况,先假设存在一个 使得

正确结果的 与 的内积比非正确结果的内积都要大一个 。
不失一般性,假设 ,假如我们找到了一个 ,它可以让我们的数据可分,那我们对这个 做归一化,把它的长度变成1的话,它一样还是可以让我们的数据可分。
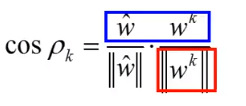
我们看下 与 之间的关系,如果我们计算这两个向量的夹角,这个夹角记为 ,我们会发现当 越来越大的时候,夹角越来越小。
我们可以计算 (夹角越小, 值越大)

在
之间,当
越来与小,
的值越来越大。
而
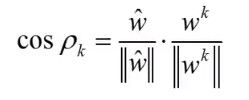
接下来看下 的值。
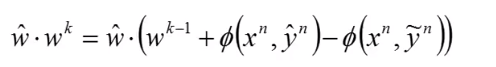
我们把右边的括号展开会发现
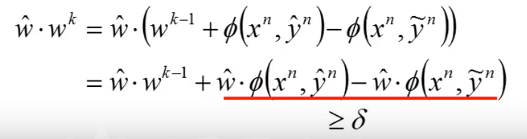
红线标出的这项一定大于等于一个
。这是来自我们的定义,现在
可以让我们的数据可分的,那不管找到一个怎样的
,它与
的内积一定比
与
的内积还小一个
。
所以红线的两项相减得到的结果是大于等于一个 的。
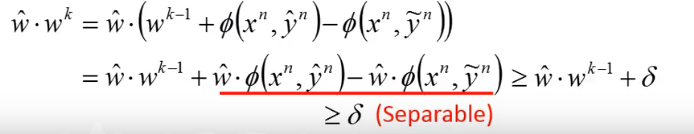
所以我们可以说 。
因为初始 。
。
所以 可以说
而
所以
同理
也就是看 的分子的话,它是不断增加的。
接下来我们再算下分母的 ,因为我们已经假定 。
如果我们发现 没有很快的增加,而这两向量的内积又增加的话,我们就可以知道 和 是越来越接近的(随着 的增加)。
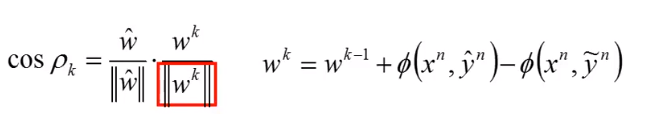
还是用这个 的表达式
当成一项,剩下的当成另一项,把平方展开得到:
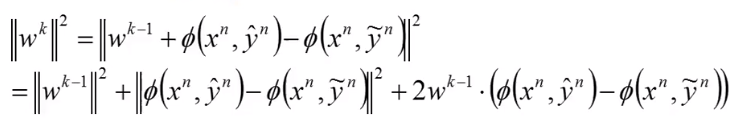
展开完后,首先红线标出的式子是一个长度,它一定大于0:
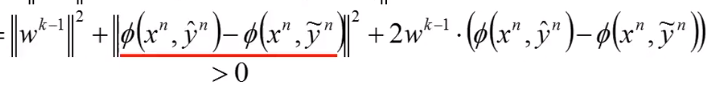
那右边的这项应该是什么样的值呢
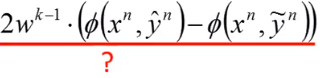
上面这项是小于0的,在预测错误的情况下, 的方向和更新方向的夹角是大于90度的,所以小于0。
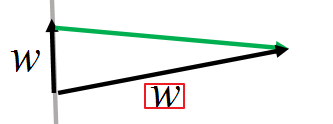
以上篇文章中更新 的图为例,更新方向向量是绿色的,预测错误的 是向上的那个,它们的夹角是大于90度的。

我们假设任何两个数据点的距离是小于
的。
所以
于是我们可以得到
长度的上界。
我们知道:
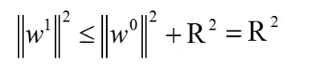
而
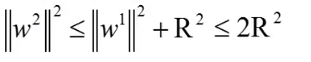
以此类推
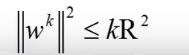
我们现在得到的结论是:
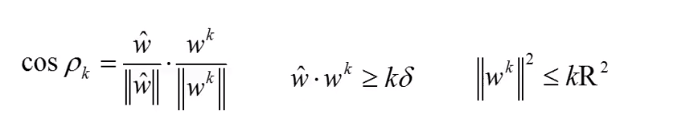
也就是说内积不断增加,而
的长度并没有增加的很快:
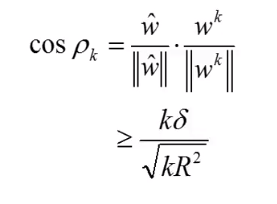
上式为什么是 呢,因为 取最大值,作为分母的话,就是使得整个式子最小,而分子又是取的最小值,所以上式是 。
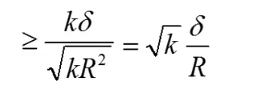
随着
不断增加,这个
的值可能会增加,我们知道
函数的值最大只能是
。
它的上边界就是
。也就是:
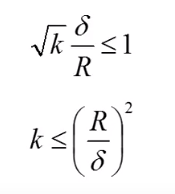
证明完毕。
从这个式子我们可以发现什么呢

如果 越大,那么这个式子的结果越小,也就是训练的越快。这很合理,如果红色的点与蓝色的点分得越开,我们训练的就越快。
但是在实际情况中我们很难找到正确和错误的结果是可分的。常见的都是不可分的情况,接下来我们就一起看下这种情况。
不可分的情况
在不可分的情况中,还是会有一些权值 比其他的要好。
假设没有任何一个向量可以让正确答案和错误答案被分开。但是在这些向量里面,
我们还是可以区分出好坏的。
假设我们有一个向量 ,它把正确答案排在第二。

有另外一个向量 ,它把正确答案排在最后一名。

虽然这两个向量都无法让正确答案的分数高过错误的,但是显然
是更好的。
那我们如何用式子来描述这种情况呢
我们可以定义一个损失 来评估 有多差,然后选择使得损失 最小的 。
的定义可以是全部的
里面,可以让最大
的值,减去正确的
所形成的值
。

从图上可以看出,就是第一名的值减去正确的结果的值,这是很直观的。
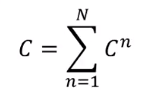
对每份数据都有一个 ,累加起来就得到了 。
我们来想下这个值有可能是负数吗,如果正确的红色框框排在第一名的话,那就变成自己减去自己,最小就是0了。
接下来如何找到一个 去使 最小呢

其实我们用梯度下降就好了,虽然这个 里面含有 。在maxout网络中我们已经看到过类似的解法:

虽然里面有个
,还是可以计算对
的梯度的。

当
不同的时候,选出来的
是不一样的。
可以把
所形成的空间想象成如下:

这个空间其实是被 切分成好几块的,比如 形成的 区域是下面涂蓝色的部分:

当 的值落在蓝色区域内,得到来的 是 。
在每个区域里面的函数是可以容易的算出来的,比如在蓝色区域的式子就可以写成这样:
其他区域也是一样的:

在每个区域里面都是可以微分的。

接下来就可以用梯度下降法来找到使
最小的

假设更新 次,做随机梯度下降。

首先要知道落在哪个区域里面(上面应该是
,
只是一个最大值,加上
才会返回一个
),然后我们算出来是在
的区域里面。
所以算梯度就简单了

然后我们就可以更新

如果把学习率
设成
,那我们做的就是structured perceptron。
就是下图这个算法:

考虑错误
我们刚才的损失函数,对所有错的情况都是一视同仁的。

但事实上并非如此,因为输出有很多种可能,在这些可能情况里面,有一些和真实的输出是很接近的。
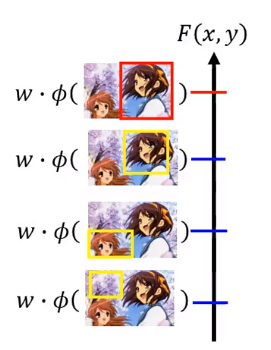
比如正确的是红框,但是你的系统框出的是第二名的那个,其实它也是框在了练功春日上面,也是可以接收的。但是其他的错误框框就无法接受了。
所以不同的错误之间还是有差别的。我们应该把这件事情考虑进去。
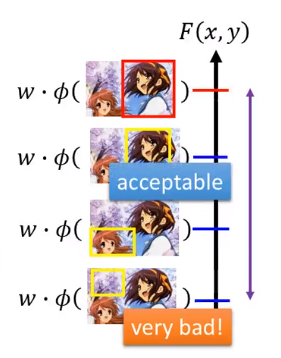
比如说,框在樱花树上是很差的,不能接受的,但是第二名那个是可以接受的。我们希望框在樱花树上的分数很低,而第二名的分数要能和正确的结果分数接近。
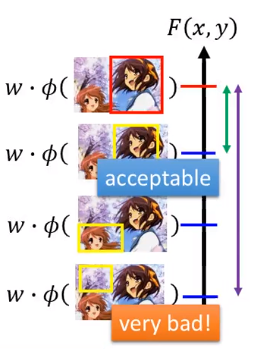
如果你今天的权重能做到,使得结果能按照框框的好坏来排序,那么训练的结果是比较安全的。假如你的测试数据和训练数据有一些差距的话,虽然你得到的第一名不是正确的,但是至少能保证分数比较高的和正确的差距不是很大。
那如果把这件事情考虑到损失函数中去呢

正确的框框是红色的,这里有两个错误的框框。当错误的框框和正确的框框很像时,我们希望第二名那个错误的框框分数与正确框框的分数差距是比较小的;而错误很离谱的第三名那个框框和正确的框框分数差距是较大的。
现在的问题是如何衡量框框的好坏。其实这是与任务有关的,在不同的任务中你要想办法去定义它。
我们用
表示正确的框框和其他框框之间的差距。
至于这个
的式子需要你自己去定义,我们假设下面的讨论中定义如下:

代表
这个框框的面积。如果某个框框和正确的框框相交的面积越大的话,并且它们面积的并集也不是很大,我们就可以得到一个比较小的差距。
那有了 以后,我们需要修改损失函数。
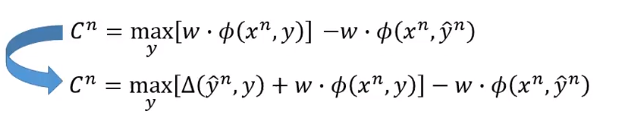
现在评判的方法是用 的分数 再加上 ,然后再减去 正确结果的分数
我们会看看哪个 ,它不止是分数大, 也大,我们才会觉得它是真正的第一名。然后我们会拿这样的 来减去 的分数。
可以想象成,如果今天有个
的
值很大,我就希望它和正确答案的分数差距越大越好。

反之如果今天有个框框,它和正确的框框其实很像的话,那就算它们的分数没有拉开也没关系。

那看下 在什么状况下会得到0,当正确的 所得到的分数,不仅是比其他的 还要到,而且都要大过一个损失函数所形成的 值的时候,那你的 会是最小的。

这个
所形成的差距就是margin。如果
是一个很不好的框框,那么它和正确答案之间的margin就会很大;反之是个可以接受的框框,那么它和正确答案之间的margin就要比较小。
我的理解是,这个 相当于是一个惩罚项,它惩罚那些 值很大的框。
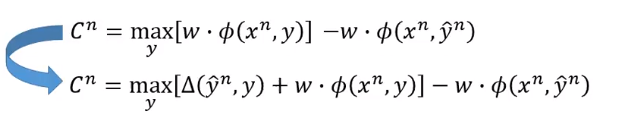
现在加上了 的这是式子如何用梯度下降去优化它呢
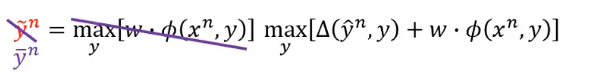
现在找的是让
加上
最大,找出来的
记作
。
梯度的计算也变了
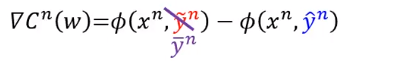
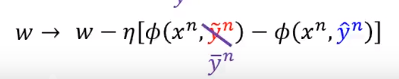
下面这个损失函数其实有另外一个观点来解释。
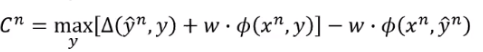
这个观点认为这个损失函数是训练数据上的误差的上界。
当你在最小化这个损失函数的时候,你是在最小化训练数据误差的上界。
最小化上界并不一定代表说误差会变小,但是是有可能会跟着变小的。
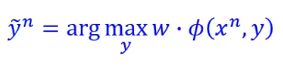
假设我们让上面这个内积最大的
,当做我们系统的输出。
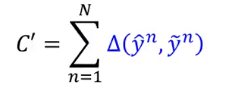
那我们希望最小化的是
,我们希望能找到一个
,让
与
之间的差距越小越好。
但是最小化 这件事情并没有那么容易,因为 可以是任何的对象; 可以是任何的函数。如果 比那些不可微分的函数更复杂,比如是阶梯状的,那么梯度下降法就无能为力了。 可以想象是对 做了一点改变,但是对 一点影响都没有。
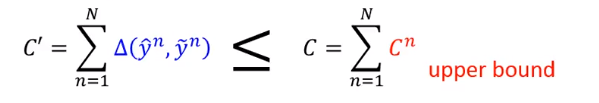
不过还好有我们刚才可以用来做损失函数
,它是
的上界,我们希望通过最小化
来达到最小化
的效果。
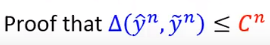
接下来证明 是 的上界。
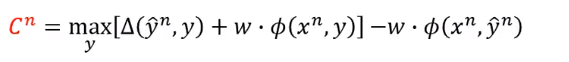
首先看下面这项是大于等于0的。
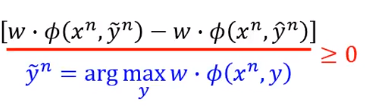
因为 是可以让 最大的 。
所以不管减去什么,一定是大于等于0的。
所以下式是成立的:
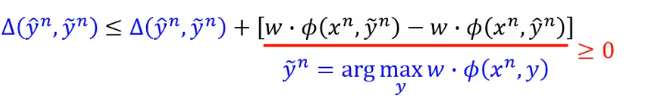
接下来换下右边这项括号里的内容:
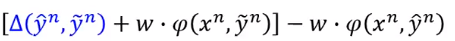
然后我们说它是小于含
的那项的
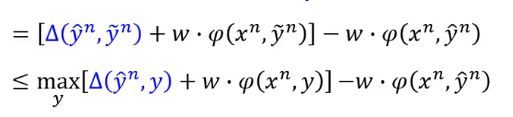
本来是计算
的
加上
的内积,现在变成了找一个
,它使得
加上内积最大。
既然这个
是
加上内积最大的那个
,它一定大过
。
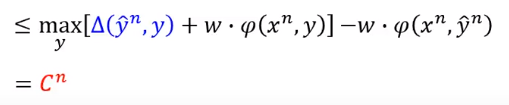
而包含
的这一项就是
。

证明完毕。
其实还有别的方法可以让
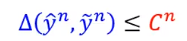
成立。
刚才说的是这个:
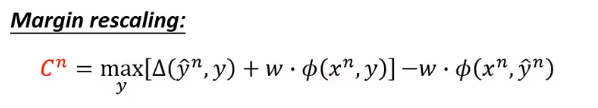
还有下面这种方法:
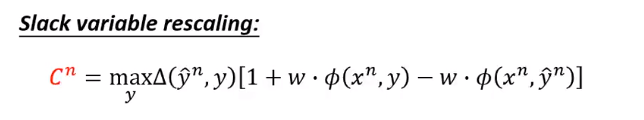
正则项
接下来再加上正则项。
训练数据和测试数据可能有不同的分布, 如果和0比较接近的话,就可以最小化这种不匹配的影响。
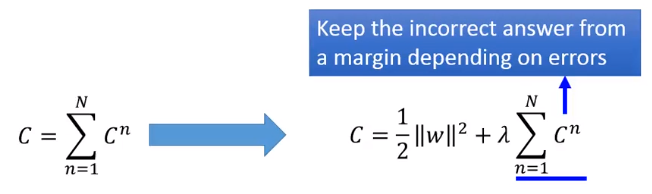
在原来的损失函数中加上 。蓝色下划线这一项是要让错误的 和正确的 之间差一个margin。

前面绿色下划线这一项就是正则项,它希望
接近0。这两项中间会有一个
,来调整这两项的差距。
那右边新的这一项如何做优化呢

优化过程如上。
接下来看看为什么今天讲的这个东西叫结构化支持向量机。
结构化支持向量机
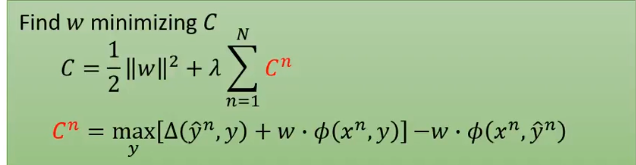
最后我们用的损失函数是这样的。我们可以稍微修改下这个式子。
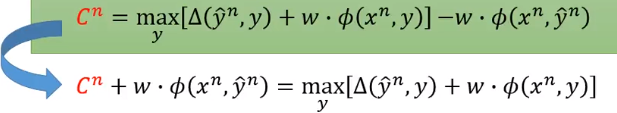
首先把右边的负号项移到左边。

把上面那项改成对所有的
,都有
大于等于
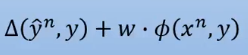
它们是一样的吗

我们今天要最小化
,那我们就说这一项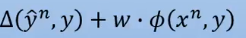
就等于
就好了。如果这一项比
大的话,就不是最小化的值。
(这里其实没有看懂,李老师讲的SVM不好理解啊)。
接下来把 移到右边
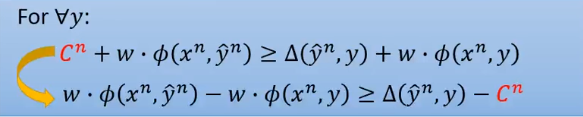
现在就变成这样

习惯上这里会把
换成

这个
称为松弛变量(Slack variable)。
在下面这个等式中,定好 后, 的值并没有直接决定,所以我们要改下描述。

现在要解的问题就变成了蓝框框出的问题:

当
时
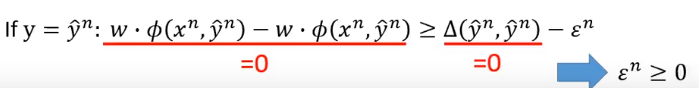
得到
。
所以可以重新描述下上面蓝框中的不等式。

如果听不懂的话,李老师说我们可以换个说法。

我们希望正确的框得到分数和错误的框得到分数中间差了个margin。如果它们的差越大,那么margin就要越大。
反之如果它们的差越小,那么margin就应该越小。
我们把红框和黄框的 当做它们之间应该有的差,如果它们越相近,那么margin就应该越小。
所以我们可以列出一个限制条件,说我们今天要找到的 应该满足以下条件。

因为我们有非常多个黄框,所以不等式也有非常多个。所有不等于
的
都会有一个不等式。
但是有一个问题是你可能找不到一个 让上面的不等式都满足。
所以我们把margin改的小一点,把margin都减去一个

为了把margin变小,这个
要是大于等于0的。

因为margin变小了,也就说要找的
的限制被放宽了。所以叫
为松弛变量。
当然限制不能放得太宽,可以想象说今天 是无穷大,那么所有的margin都变成负值,那么随便找到一个 都会让这些不等式被满足的话,这个就不是我们要的东西。
我们希望放宽的幅度必须是最小的,也就是说我们希望 的值能越小越好。

假设我们今天有两笔数据, 和 。对 来说,我们希望正确的减掉错误的要大于它们之间的 减掉 。对所有的 除了 以外,这些不等式都成立。

接下来有另外一笔数据 ,我们希望正确的减掉错误的一样大于 减掉 。
在满足这些不等式的前提下,我们希望这些 的和是最小的。
这样得到的式子就和刚才推导出来的是一样:

这个东西和SVM的关系是什么呢,它和SVM的式子其实是大同小异的。它们都是二次规划问题。
现在唯一的问题是限制条件太多了,接下来的问题是,在限制这么多的情况下应该要怎么办。且听下节分解。
分割平面法
现在的问题是,我们有一个参数空间,由 和 所形成。

参数空间上面的颜色代表需要最小化的 值:
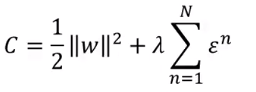

在没有限制的情况下,青色星星这一点是最小值。但是我们有大量的限制条件。

这些限制告诉我们,在这个空间里面只有中间那个灰色区域是符合我们所有的限制的。

我们要在灰色区域中找最小值,我们得到的结果就是上图青色星星那一点。限制的问题是如何找出这个灰色区域。
虽然这里的限制很多,但是大部分的限制都是冗余的。

比如说我们看这两条红色的限制,我们只要有这两条红色的限制,就能决定大部分灰色区域的形状。这样下面绿色的这条限制,其实是不会对结果有影响的。

所以我们可以优化下限制条件表达式,不需要穷举所有的
了。我们只需要从有影响的限制条件集合中去取。
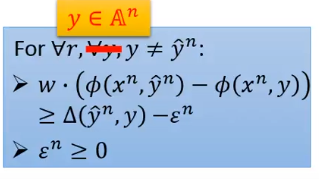
这个小部分的有影响的限制条件集叫工作集(working set),这里用
表示。
如果有能找出这样的工作集的话,在优化的时候我们只要考虑 里面的 。
现在的问题是如何找到这个工作集。我们通过迭代的方法来找,每次找到一个元素加到工作集里面。
一开始为每个样本初始化一个空工作集,然后根据这个工作集去解下面的问题:

我们考虑工作集里面的
,假设我们根据这个工作集解出一个
后,我们再用这个
去重新检查下,增加新的元素到工作集。此时工作集就不一样了。然后我们再用这个工作集去重新解上面的QP问题。
这样又可以得到不一样的 ,又可以找到新的成员添加到工作集。就这样一直循环。
我们用图示的方式来解释下这个过程是如何运作的。
- 先假设初始化样本 的工作集为 ,表示它是空集合,也就是没有任何限制;
- 假设我们在没有限制的情况下,得到的结果是蓝色的点。

- 找出这个蓝色的点后,我们需要看看有哪些限制是没有被满足的。比如下图这些红色的线都没有被满足

- 虽然有很多没有被满足的限制,但是我们只选择没有满足的最严重的那个。假设我们找到的是下图红线那个,并记这个限制为

- 我们就把这条限制加到工作集里面,现在工作集就有一个成员了。
- 根据我们现在工作集唯一的成员,它告诉我们说,最小的值是下面蓝色星星

- 接下来我们以蓝色星星作为结果,看还有哪些限制没有被满足。此时还有很多,比如新的红线就没有被满足

- 再把这条没有被满足的限制(就是上图没有经过蓝色星星的那条红线)加到工作集中。我们就根据现有的两条限制,得到一个新的值:

- 接下来要继续检查还有哪些限制没有被满足,比如说下面这条新的线就没有被满足。

- 再把这条新线加到工作集中,现在工作集中有3条线了,我们就根据这3条线,得到一个新的最小值。

- 于是就找到我们要的解,就结束整个算法
上面有个问题就是如何寻找没有满足的最严重的那个限制。

我们先来看下限制的表达式,当一个限制被违反(violate)的时候,给定
,就是说
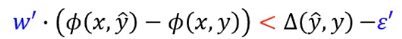
但是不满足(违反)的限制可能有很多个,我们要定义一个违反的程度:
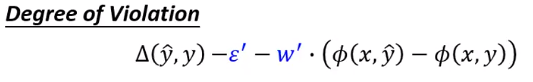
就是不等式右边这一项减去左边,它大的越多就越违反。
我们还可以简化下这个式子,对所有的
来说,
是一个固定的值,它与
没有关系,而
也不影响我们计算。因此可以简化为:

最后违反程度最严重的
就是可以让上式的值最大的
:
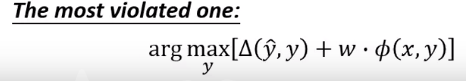
我们现在来看下这个分隔平面法的样子:

这里用
表示当前找出的违反程度最严重的限制。知道我们无法找出一个新的
放入工作集时,整个算法就结束了。
用结构化SVM来做多分类和二分类
多分类SVM
假设有
个类别,有
个权重,它们组成一个权重向量。

就可以写成
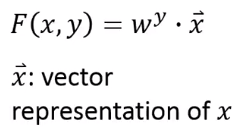
这个
就是我们要去分类的数据,用向量表示。
如果我们用结构化SVM的是,一般
是长这样的:
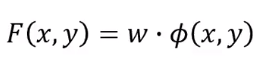
那和下面这个公式是同一个吗
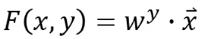
其实它们是同一个。我们可以把
用列向量的形式表示,
写成这样:

在
,
放的位置与
的取值有关,假设这里
,我们把
放到这个位置。
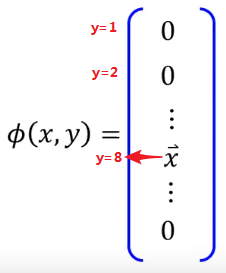
因此这两个式子是可以一样的。

那推断类别的时候怎么做呢,就是穷举所有可能的
,看哪个的
的取值最大。因为类别是有限的,所以这里的穷举很容易。
解下来就做一下训练。此时的限制条件是有限的。所以也用不着分隔平面法。

那有多少个限制呢,假设有
份训练数据,每份训练数据都有
个不正确的
。因此整个限制的数量就是
。
根据上面
的形式,我们可以把
乘进去:
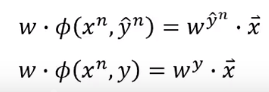
得到上面两项,然后代入限制条件公式中:

那这里的
是什么呢,这个其实可以自己定义。可以说如果我们预测的类别和真实类别不一样就是1,一样就是0。
但是可以考虑另外一种问题,就是某种类型当成另一个类别是比较严重的,而当成其他某种类别是不严重的。
比如说
有狗、猫、公交车和小汽车。
然后我们就可以自己定义,本来类别是狗,我们预测的是猫,相差就不是很严重;而本来是狗,预测的是公交车,相差程度就很大。
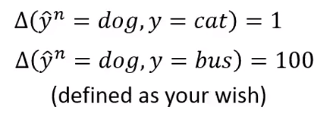
这样在训练的时候,我们的模型就会尽量避免把狗识别成公交车。
二分类SVM
二分类其实就是多分类中的
而已。

本来我们的限制是写成这样的,但是因为我们只有两个类别。我们就可以把正确答案是类别1,弄错成类别2与正确答案是类别2,弄错成类别1的
不一样。

我们这里假设只要弄错
。今天我们
,你会发现只有两种情形:
- 要么它属于类别1
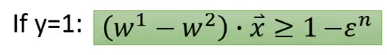
- 要么它属于类别2
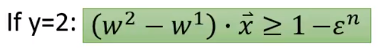
我们可以假设 而 ,代入上面就可以得到。

