2019斯坦福CS224n深度学习自然语言处理笔记（3）——分类模型与神经网络

课程视频链接：《 深度学习与自然语言处理（3）》
前两章算是引言，主要介绍了什么是自然语言处理，以及自然语言处理中最基础的工作——如果和表示词的意思的相关工作。接下来，主要介绍一下分类模型和神经网络，并以命名实体识别举例说明神经网络的运行过程。最后简要介绍一下矩阵运算。

1. 什么是分类？

为了给没有基础的同学介绍一下背景，这里首先简要介绍一下分类。所谓的分类就是给定输入X，通过分类模型后，获得输出y，其中y是一个离散的值（可能有2个值，也可能有10个值），有多少值就是多少个类别。这个过程就是分类。

其过程实现在机器学习中，一般使用softmax（多分类）和logist（二分类）。

1.1 logist（二分类）

一般的，如果一个模型是二分类模型时，可以使用逻辑斯蒂回归Logsit进行二分类，唯一需要注意的是，我们使用逻辑斯蒂回归时，给出的结果是概率（0-1之间的数），需要我们最后做转换后，才能进行二分类。

这里我们不详细解说，具体的可看《逻辑斯蒂回归》。

1.2 softmax（多分类）

对于softmax之前没有太多的介绍，这里详细讲述一番。softmax函数是用来处理多分类的，可以说，它是logist的一般形式。但是和逻辑斯蒂回归又有些许不同。

1.2.1 softmax函数

我们首先给出softmax函数的样子：
$P(Y|X)=\frac{e^{W_yX}}{\sum^C_{c=1}e^{W_cX}}$
值得注意的是，这里的W有C个，其中C为类型的数量，也就是说，它相当于训练了多个二分类的模型，但是该如何在同一个模型中融合呢？softmax函数的融合办法是，让所有的类别预测的概率取对数后归一，这样会使得概率越大的类型的概率趋近于1，其他的类别概率趋向于0。

1.2.2 独热编码

在具体的操作中，我们一般把多分类的类别使用独热（one-hot）编码，在训练预料中，类别标签中只有1个类别为1，其余为零，分别表示该类型的概率。而在预测的时候，则会有一个较大的类别趋近于1，其他的都是趋近于0的。以三分类为例，真实值的类别为2。

类型名	类别1	类别2	类别3
真实值	0	1	0
预测值	0.05	0.9	0.05

1.2.3 交叉熵

这样，我们在训练模型时，仍然采用最大化正确概率的思想，这里使用交叉熵作为损失（Loss）函数来实现。
交叉熵的公式如下：
$H(p,q)=-\sum^C_{c=1}p(c)logq(c)$
其中，p( c )表示该类型的真实概率，q表示该类型的模型概率，我们的目标就是想让p和q的概率分布一致。

从softmax的公式代入即可获得：
$Loss=H=-\sum^N_{n=1}p(n)logq(n)=-\sum^N_{n=1}y_nlog\frac{e^{w_nX}}{\sum_{c=1}^Ce^{w_cX}}$

由于 $y_c$中只有1个为1，其余为0，则此Loss函数退化为:
$Loss=y_nlog\frac{e^{w_nX}}{\sum_{c=1}^Ce^{w_cX}}$
其中n为概率为1的那个。

1.2.4 反向传播

然后在训练时，其反向传播方法仍然使用梯度下降法，即：
$w_n^{new}=w_n^{old}+\alpha\frac{\partial Loss}{\partial w_n}$
其中 $\alpha$为学习率，那么为啥要带个 $w_n$呢？我们知道Loss里有C个w，我们每次只更新目标类别的w即可。

更多有关softmax的可以参考《softmax求导训练过程》和《softmax回归介绍》。

2.神经网络模型

神经网络模型来源于生物学中对于神经元的模拟，生物学中神经元结构如下图：

神经网络模型中的神经元形式如下：

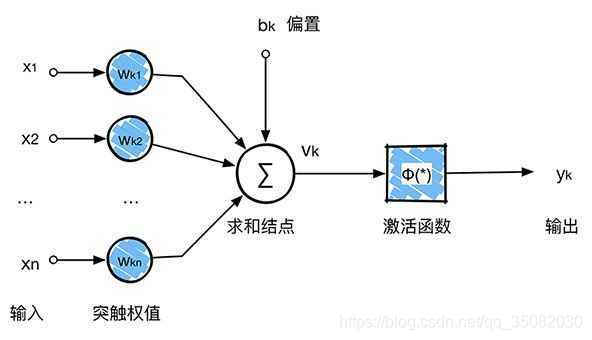
看起来是不是很像，也仅仅是很像了，具体的神经元的运行机制目前还并不清楚。因此，神经网络模型中的单个神经元的形式化表示如下，这里将偏置也并入 $x_0$中。：
$Y=f(\sum w_ix_i)$

2.1 神经网络模型与逻辑斯蒂回归有什么不同？

上节所说的神经元看似和逻辑斯蒂回归比较像，完全可以被模拟：
$h_{w,b}=f(wx+b)$
$f(z)=\frac{1}{1+e^{-z}}$
那么，神经网络模型与逻辑斯蒂回归有什么不同？

相比较传统的逻辑斯蒂回归，最基础的神经网络就已经具有两个方面的进步，第一个进步是多个神经元（cell）可以认为是多个逻辑斯蒂回归同时运行，每个神经元都可以得到一个划分界面。第二个进步则是多层化，多个神经元的层叠就可以获得更细致的划分。第三个进步是拥有激活函数可以使得整个模型呈现非线性。

第一个进步可以说是可以从不同角度对同一事物进行特征捕捉，所谓横看成岭侧成峰，但是像我们双眼一样，使用不同角度才能够看到事物的真正面貌。这是普通神经网络的第一个进步。第二个进步则是可以使得判定条件更丰富，即每多一层，就可以在该层次上进一步划分类型。第三个进步则是使用了激活函数，使得函数可以区分非线性数据，就像曾经说的，它可以使得数据划分界限变得弯曲，从而能够更好的拟合数据类型的分布。

第一个进步的图像化表示为如下图所示，每多一个神经元，就可以多一道分割线：

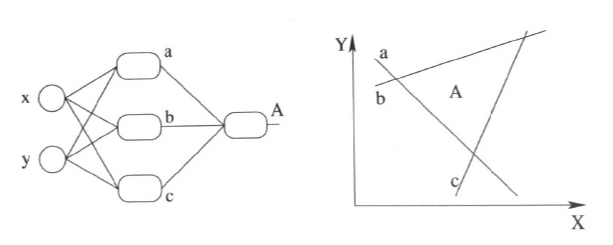
第二个进步还是上图所示，只不过多层的结果可以使得判定层次化，例如A的作用其实就是在已划分的7个界面上重新定义每块区域上的类型。若再多一层，可以继续对于已划分的区域进一步划分。

第三个进步则是使得划分平面变为曲线，如下图所示，这样，对于数据的拟合更加切实际，而且也能解决线性不可分等问题。

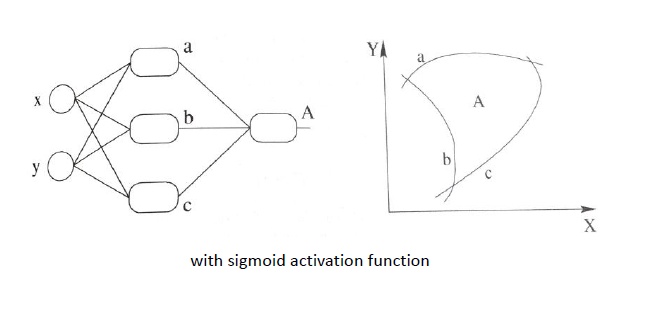
更多关于此节内容的可以参见《激活函数的作用》以及《神经网络解决异或问题》等。

3. 命名实体识别（NER）

由于英文中不需要进行分词，因此直接使用命名实体识别进行神经网络模型举例，这里列举出原PPT中的例子（由于网上其他例子均不直观）。

命名实体识别的任务就是在给出的一个文本中，找到实体并区分其实体是人名（PER）、地名（LOC）、组织名（ORG）等。看起来是不是挺简单的。

命名实体具有以下作用：

1. 追踪某一特别的实体的文章（比如包含“四川凉山”的文章，肯定都是和四川凉山火灾大致相关的文章，在这里向牺牲的英雄致敬！）
2. 用于问答，比如问火灾是在哪里发生的？回答凉山。
3. 构建实体之间的关系，比如小说里各个角色之间的关系等。
4. 其他各种槽填充任务（多轮对话的任务中可以使用）

命名实体识别的方法有很多，包括基于规则方法、基于特征匹配方法，和基于神经网络的方法，具体的可以参见《命名实体识别解决方法》。这里我们介绍最为简单的一种方法，根据窗口的词向量进行中心词是否是实体，其模型如下：

这样问题就转换为，给定5个单词，判断中心单词是什么类型即可。像上一章中讲的一样，使用词向量作为输入，然后使用softmax进行多分类即可。接下来将要介绍如何使用梯度下降法进行训练。

3.1 梯度下降（手动）

这里使用手算梯度下降，来清楚了解具体是如何运算的，下一步则是自动的反向传播。

首先，若有一个输入，一个输出：
$f(x)=x^3$
$\frac{df}{dx}=3x^2$

若有若干个输入，但是只有一个输出:
$f(\bold x)=f(x_1,x_2,...,x_n)$
$\frac{\partial f}{\partial \bold x}=[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...,\frac{\partial f}{\partial x_n}]$

若有若n个输入，m个输出：
$\bold f(\bold x)=[f_1(x_1,x_2,...,x_n),f_2(x_1,x_2,...,x_n),...,f_m(x_1,x_2,...,x_n)]$
$\frac{\partial \bold f}{\partial \bold x}=\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}$
这里可以知道 $(\frac{\partial \bold f}{\partial \bold x})_{ij}=\frac{\partial f_i}{\partial x_j}$

这样，我们就可以考虑链式法则了。
对于简单的求导，多个求导即可：
$z=3y$
$y=x^2$
$\frac{\mathrm{d}z}{\mathrm{d}x}=\frac{\mathrm{d}z}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm{d}x}=6x$
对于多个输入的求导，使用多个雅克比矩阵即可，这里x的维度是m* 1，W的维度是n* m：
$\bold h=f(\bold z)$
$\bold z=\bold W\bold x+\bold b$
$\frac{\partial \bold h}{\partial \bold x}=\frac{\partial \bold h}{\partial \bold z}\frac{\partial \bold z}{\partial \bold x}$

那么雅克比矩阵计算方法是什么呢？我们以一个例子来说明。
$\bold h=f (\bold z)$
$h_i=f (z_i)$
$(\frac{\partial \bold h}{\partial \bold z})_{ij}=\frac{\partial h_i}{\partial z_j}=\frac{\partial f(z_i)}{\partial z_j}$
可得，若i=j则为 $f'(z)$,否则为0。
这样就可得
$\frac{\partial \bold h}{\partial \bold z}=\begin{bmatrix} f'(z_1) & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & f'(z_n) \end{bmatrix}=diag(f'(z))$

至于其他部分的雅克比矩阵求导如下：
$\frac{\partial \bold z}{\partial \bold x}=\frac{\partial \bold W\bold x +\bold b}{\partial \bold x}=\bold W$
$\frac{\partial \bold z}{\partial \bold b}=\bold I(单位矩阵)$
$\frac{\partial \bold s}{\partial \bold u}=\frac{\partial \bold u^T\bold h}{\partial \bold u}=\bold h^T$

现在还是回到我们最初的神经网络，以最简单的 $\frac{\partial s}{\partial \bold b}$尝试求解。
原有的公式为：
$s=\bold u^T \bold h$
$\bold h=f(\bold z)$
$\bold z=\bold W \bold x+\bold b$

则所求的 $\frac{\partial s}{\partial \bold b}$为，这里 $u^T$维度为1*n, $diag(f'(z))$的维度是n *n：
$\frac{\partial s}{\partial \bold b}=\frac{\partial s}{\partial \bold h}\frac{\partial \bold h}{\partial \bold z}\frac{\partial \bold z}{\partial \bold b}$
$=\bold u^T diag(f'(z)) \bold I$
$=\bold u^T\circ f'(z)(这个不用看)$

同样的,这里的W是n*m维。
$\frac{\partial s}{\partial \bold W}=\frac{\partial s}{\partial \bold h}\frac{\partial \bold h}{\partial \bold z}\frac{\partial \bold z}{\partial \bold W}$

可以看到有两个部分是一样的,其大小为:
$\frac{\partial s}{\partial \bold h}\frac{\partial \bold h}{\partial \bold z}=\delta$

如果是nm的雅克比矩阵，则计算如下,应该是一个n*m的矩阵：
$\frac{\partial s}{\partial \bold W}=\begin{bmatrix} \frac{\partial s}{\partial W_{11}} & \cdots & \frac{\partial s}{\partial W_{1m}} \\ \vdots & \ddots & \vdots \\ \frac{\partial s}{\partial W_{n1}} & \cdots & \frac{\partial s}{\partial W_{nm}} \end{bmatrix}$
最终：
$\frac{\partial s}{\partial \bold W}=\delta^T\frac{\partial z}{\partial \bold W}=\delta^T \bold x^T$

这里硬核较多，需要仔细阅读才能够理解。