第一篇 强化学习基础（下 ）——基于模型的动态规划算法

---

本分类专栏博客系列是学习《深入浅出强化学习原理入门》的学习总结。
书籍链接：链接：https://pan.baidu.com/s/1p0qQ68pzTb7_GK4Brcm4sw 提取码：opjy

---

---

---

基于模型的动态规划算法

1. 强化学习的分类概述

强化学习的⽬标是找到最优策略 $π$使得累积回报的期望最⼤。所谓策略是指状态到动作的映射 $π：s→a$，⽤ $τ$ 表⽰从状态 $s$ 到最终状态的⼀个序列 $τ：s_t ，s_{t+1} …，s_T$ ，则累积回报 $R （τ）$是个随机变量，随机变量⽆法进⾏优化，⽆法作为⽬标函数，我们采⽤随机变量的期望作为⽬标函数，即 $∫R(τ)p_π(τ) dτ$作为⽬标函数。⽤公式 $\mathop {\max }\limits_\pi \int {R(\tau ){p_\pi }(\tau )d\tau }$来表⽰强化学习的⽬标： 。强化学习的最终⽬标是找到最优策略为 $π^* ：s→u^*$ ，我们看⼀下这个表达式的直观含义。

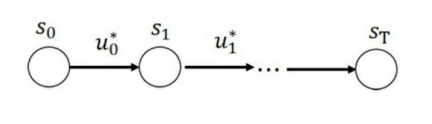
如上图所⽰是序贯决策⽰意图，最优策略的⽬标是找到决策序列 $u_0^* \to u_1^* \to ... \to u_T^*$ ，因 此从⼴义上来讲，强化学习可以归结为序贯决策问题。即找到⼀个决策序列，使得⽬标函数最优。

累积回报的含义是评价策略完成任务的总回报，所以⽬标函数等 价于任务。强化学习的直观⽬标是找到最优策略，⽬的是更好地完成任 务。

在上⼀节，我们已经将强化学习纳⼊到⻢尔科夫决策过程MDP的框架之内。⻢尔科夫决策过程可以利⽤元组 $（S，A，P，r，γ）$来描述，根据 转移概率 $P$是否已知，可以分为基于模型的动态规划⽅法和基于⽆模型的强化学习⽅法，如图3.2所⽰。两种类别都包括策略迭代算法，值迭代算法 和策略搜索算法。不同的是，在⽆模型的强化学习⽅法中，每类算法⼜分为online和offline两种。online和offline的具体含义，我们会在下⼀章中详细介绍。

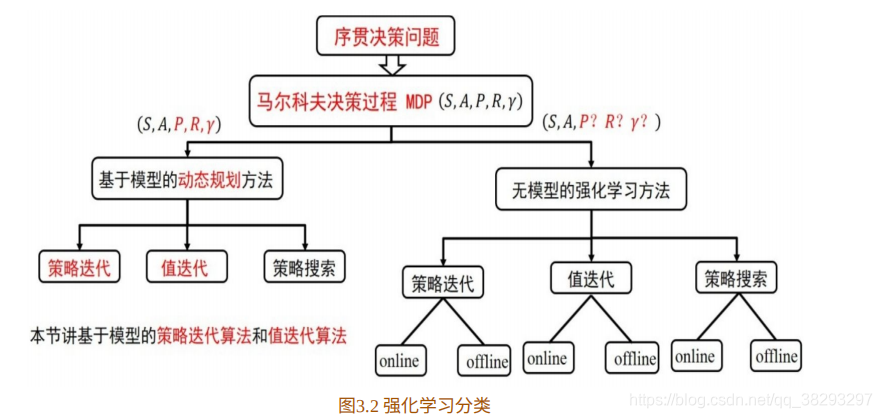
2. 基于模型的动态规划方法理论

基于模型的强化学习可以利⽤动态规划的思想来解决。顾名思义，动态规划中的“动态”蕴含着序列和状态的变化；“规划”蕴含着优化，如线性优化，⼆次优化或者⾮线性优化。

利⽤动态规划可以解决的问题需要满⾜两个条件：⼀是整个优化问题可以分解为多个⼦优化问题；⼆是⼦优化问题的解可以被存储和重复利⽤。

前⾯已经讲过，强化学习可以利⽤⻢尔科夫决策过程来描述，价值函数分为状态值函数和状态-行为值函数，关于 $v_\pi(s)$和 $q_\pi(s,a)$的贝尔曼方程如下：

其描述了当前状态值函数和其后续状态值函数之间的关系，即状态值函数（动作值函数）等于瞬时回报的期望加上下一状态的（折扣）状态值函数（动作值函数）的期望。

扫描二维码关注公众号，回复： 10455655 查看本文章

强化学习的目标是找到一个最优策略，使得回报最大。准确的说是使值函数最大，包括状态值函数和动作值函数，分别记为 $v_*(s)$和 $q_*(s,a)$

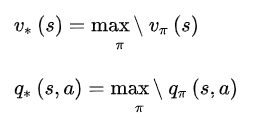
对于任意一个MDPs，总是存在一个最优的策略 $\pi_*$，在使用这个策略时就能取得最优值函数，即 $v_{\pi_*}(s)=v_*(s)$和 $q_{\pi_*}(s,a)=q_*(s,a)$，利⽤⻉尔曼最优性原理得到⻉尔曼最优化⽅程

从⽅程（3.1）中可以看到，⻢尔科夫决策问题符合使⽤动态规划的两个条件，因此可以利⽤动态规划解决⻢尔科夫决策过程的问题。

2.1 值函数的求解

⻉尔曼⽅程（3.1）指出，动态规划的核⼼是找到最优值函数。那么， 第⼀个问题是：给定⼀个策略 $π$，如何计算在策略 $π$下的值函数？其实上章已经讲过，此处再重复⼀遍，如图3.3所⽰：

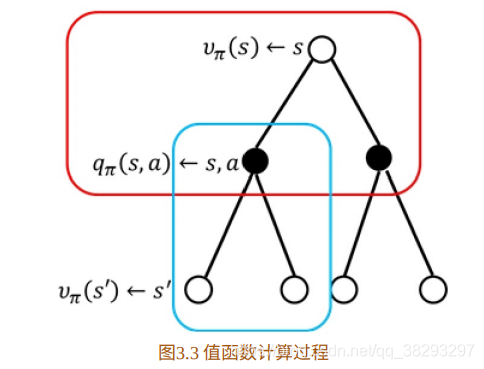
图中上部⼤⽅框内的计算公式为：

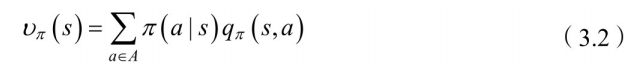
该⽅程表⽰，在状态 $s$处的值函数等于采⽤策略 $π$时，所有状态-⾏为值 函数的总和。下⾯⼩⽅框的计算公式为状态-⾏为值函数的计算：

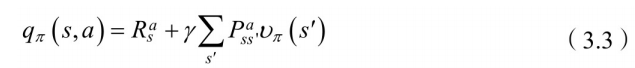
该⽅程表⽰，在状态 $s$采⽤动作 $a$的状态值函数等于回报加上后续状态值函数。

将⽅程（3.3）代⼊⽅程（3.2）便得到状态值函数的计算公式：

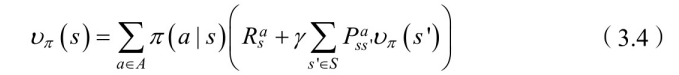
状态 $s$ 处的值函数 $v_π(s)$，可以利⽤后继状态的值函数 $v_π(s′)$ 来表 ⽰。可是有⼈会说，后继状态的值函数 $v_π(s′)$ 也是未知的，那么怎么计算当前状态的值函数，这不是⾃⼰抬⾃⼰吗？如图3.4所⽰。没错，这正是bootstrapping算法（⾃举算法）

如何求解（3.4）的⽅程？⾸先，我们从数学的⾓度去解释⽅程 （3.4）。对于模型已知的强化学习算法，⽅程（3.4）中的 $P_{ss'}^a,\gamma ,R_s^a$都是已知数， $π(a|s)$为要评估的策略是指定的，也是已知值。⽅程（3.4） 中唯⼀的未知数是值函数，从这个⾓度理解⽅程（3.4）可知，⽅程（3.4） 是关于值函数的线性⽅程组，其未知数的个数为状态的总数，⽤ $|S|$来表⽰。此处，我们使⽤⾼斯-赛德尔迭代算法进⾏求解。即：

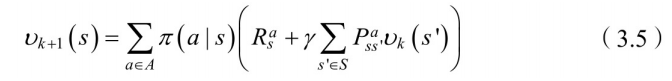
⾼斯-赛德尔迭代法的讲解请参看 3.2 节。建议读者先去学习和了解⾼ 斯-赛德尔迭代法再回来继续学习。

2.2 策略迭代算法

策略评估算法和策略改善算法合起来便组成了策略迭代算法。

2.2.1 策略评估

需要注意的是，每次迭代都需要对状态集进⾏⼀次遍历（扫描）以便评估每个状态的值函数。

接下来，我们举个策略评估的例⼦。

如图3.6所⽰为⽹格世界，其状态空间为 $S=\{1，2，…，14\}$，动作空间 为 $A=\{东，南，⻄，北\}$，回报函数为 $r=-1$，需要评估的策略为均匀随机策略：

$\pi (东| \cdot ) = 0.25,\pi (南| \cdot ) = 0.25,\pi (西| \cdot ) = 0.25,\pi (北| \cdot ) = 0.25$

图3.7为值函数迭代过程中值函数的变化。

为了进⼀步说明，我们举个 具体的例⼦，如从 $K=1$ 到 $K=2$ 时，状态 $1$ 处的值函数计算过程。

由公式 ${v_{k + 1}}(s) = \sum\limits_{a \in A} {\pi (a|s)\left( {R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{v_k}(s')} } \right)}$得到：

${v_2}(1) = 0.25*( - 1 - 1) + 0.25*( - 1 - 1) + 0.25*( - 1 - 1) + 0.25*( - 1 + 0) = 0.25* - 7 = - 1.75$
(PS：以上计算过程个人觉得有问题，东南没问题，西北应该均为 $(-1+0)$，最后因该是 $-1.5$)

计算值函数的⽬的是利⽤值函数找到最优策略。第⼆个要解决的问题 是：如何利⽤值函数进⾏策略改善，从⽽得到最优策略？

2.2.2 策略改善

⼀个很⾃然的⽅法是当已知当前策略的值函数时，在每个状态采⽤贪婪策略对当前策略进⾏改善，即

${\pi _{l + 1}}(s) \in \mathop {\arg \max }\limits_a {q_{{\pi _l}}}(s,a)$

如图3.8给出了贪婪策略⽰意图。图中虚线为最优策略选择。

如图3.9所⽰为⽅格世界贪婪策略的⽰意图。我们仍然以状态1为例得 到改善的贪婪策略：

⾄此，我们已经给出了策略评估算法和策略改善算法。万事已具备， 将策略评估算法和策略改善算法合起来便组成了策略迭代算法，如图3.10 所⽰。

策略迭代算法包括策略评估和策略改善两个步骤。在策略评估中，给定策略，通过数值迭代算法不断计算该策略下每个状态的值函数，利⽤该值函数和贪婪策略得到新的策略。如此循环下去，最终得到最优策略。这是⼀个策略收敛的过程。

如图3.11所⽰为值函数收敛过程，通过策略评估和策略改善得到最优值函数。

2.3 值函数迭代算法

从策略迭代的伪代码我们看到，进⾏策略改善之前需要得到收敛的值函数。值函数的收敛往往需要很多次迭代，现在的问题是进⾏策略改善之前⼀定要等到策略值函数收敛吗？

对于这个问题，我们还是先看⼀个例⼦。

如图3.12所⽰，策略评估迭 代10次和迭代⽆穷次所得到的贪婪策略是⼀样的。因此，对于上⾯的问 题，我们的回答是不⼀定等到策略评估算法完全收敛。如果我们在评估⼀次之后就进⾏策略改善，则称为值函数迭代算法。

值函数迭代算法（如图3.13所⽰）的伪代码为

需要注意的是在每次迭代过程中，需要对状态空间进⾏⼀次扫描，同 时在每个状态对动作空间进⾏扫描以便得到贪婪的策略。

（PS:关于max的那一块，原文中应该是少了一个括号，参考下图）

值函数迭代是动态规划算法最⼀般的计算框架，也就是说与策略迭代不同的是值迭代是根据状态期望值选择动作，而策略迭代是先估计状态值然后修改策略。

我们接下来阐述最优控制理论与值函数迭代之间的联系。解决最优控制的问题往往有三种思路：变分法原理、庞特⾥亚⾦最⼤值原理和动态规划的⽅法。三种⽅法各有优缺点。

2.4 最优控制理论与值函数迭代之间的联系

基于变分法的⽅法是最早的⽅法，其局限性是⽆法求解带有约束的优化问题。基于庞特⾥亚⾦最⼤值原理的⽅法在变分法基础上进⾏发展，可以解决带约束的优化问题。相⽐于这两种经典的⽅法，动态规划的⽅法相对独⽴，主要是利⽤⻉尔曼最优性原理。

3. 动态规划中的数学基础讲解

利⽤（3.4）计算策略已知的状态值函数时，⽅程（3.4）为⼀个线性⽅ 程组。因此策略的评估就变成了线性⽅程组的求解。线性⽅程组的数值求 解包括直接法（如⾼斯消元法，矩阵三⾓分解法，平⽅根法、追赶法等） 和迭代解法。策略评估中采⽤线性⽅程组的迭代解法。

3.1 线性方程组的迭代解法

所谓迭代解法是根据 $AX=b$ 这个线性方程组设计⼀个迭代公式，任取初试值 $X^{(0)}$，将其代⼊到设计的迭代公式中，得到 $X^{(1)}$，再将 $X^{(1)}$代⼊迭代公式中得 到 $X^{(2)}$，如此循环最终得到收敛的 $X$。

那么，如何设计迭代公式？

3.2 雅克⽐（Jacobi）迭代法

雅克⽐迭代法假设系数矩阵的对⾓元素 ${a_{ii}} \ne 0$ 。从线性方程组 $AX=b$ 的第 $i$个⽅程分离出 $x_i$，以此构造迭代⽅程：

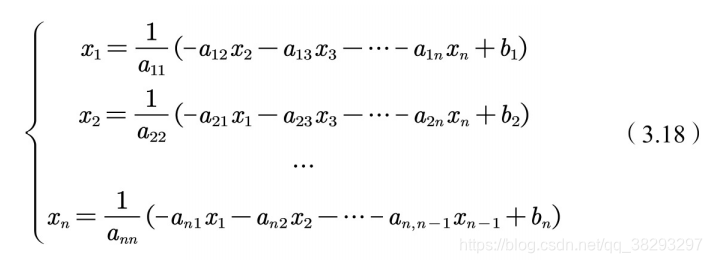
⽅程（3.18）写成矩阵的形式为

$X = - {D^{ - 1}}(L + U)X + {D^{ - 1}}b$

若记 $B = {D^{ - 1}}(L + U),d = {D^{ - 1}}b$，则迭代公式为 $X=BX+d$，在进⾏迭代计算时，（3.18）式变为，

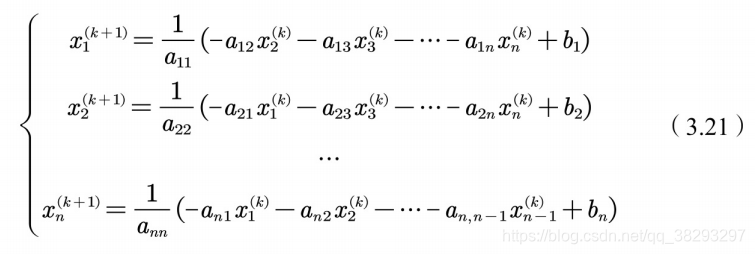
利⽤迭代公式（3.20）求解线性⽅程组（3.17）的⽅法称为雅克⽐迭代 法。矩阵B称为迭代矩阵。

雅克⽐迭代法解线性⽅程很快，还能不能更快？答案是肯定的。我们 可以观察（3.21），不难发现第 $k+1$ 次迭代计算分量 $x_i^{(k + 1)}$时，分量 $x_1^{(k + 1)},x_2^{(k + 1)},...,x_{i - 1}^{(k + 1)}$ 都已经求出来了，但是在计算 $x_i^{(k + 1)}$ 时，雅克⽐迭代⽅法没有利⽤这些新计算出来的值。如果这些新计算出来的值能够被利⽤，计算速度肯定会提⾼，这就是⾼斯-赛德尔迭代法。

3.3 高斯-塞德尔迭代法

当求得新的分量之后，⻢上⽤来计算的迭代算法称为⾼斯-赛德尔迭代法。对于线性⽅程组，对应于雅克⽐迭代过程（3.21）的⾼斯-赛德尔迭代过程为

⽤矩阵的形式可表⽰为 $(D + L){X^{(k + 1)}} = - U{X^{(k)}} + b$

若记 $G = - {(D + L)^{ - 1}}U,{d_1} = {(D + L)^{ - 1}}b$，则上式子写成迭代⽅程为

${X^{(k + 1)}} = G{X^{(k)}} + {d_1}$

4. 最优控制理论与强化学习比较

当模型已知时，强化学习问题可转化为最优控制问题。本节我们给出 最优控制的计算⽅法。⼀般⽽⾔，最优控制的数值计算⽅法分为间接法和 直接法。其分类如图3.18所⽰。

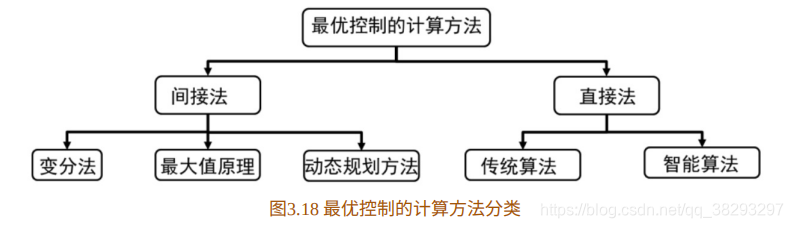
最优控制问题的数学形式化，可由⽅程（3.6）和（3.8）给出。为了表 述⽅便，我们在这⾥重复写下最优控制的数学形式化：

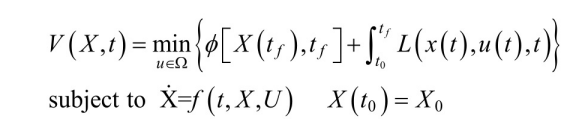
4.1 间接法

所谓间接法，是指⾸先利⽤变分法、最⼤值原理或者动态规划⽅法得 到求解最优问题的⼀组微分⽅程（如本章3.1节利⽤动态规划的⽅法得到了 ⼀组偏微分⽅程），之后，利⽤数值求解⽅法求出此微分⽅程组的解，此 解即为原最优问题的解。如本⽂介绍的微分动态规划的⽅法就属于间接 法。

4.2 直接法

直接法与间接法不同，它不需要⾸先利⽤最优控制理论（如变分原 理，最⼤值原理或动态规划⽅法）得到⼀组微分⽅程，⽽是直接在可⾏控 制集中搜索，找到最优的解。直接⽅法也分为两类，⼀类是将状态变量和 控制变量参数化，将最优控制问题转化为参数优化问题；第⼆类是引⼊函 数空间中的内积与泛函的梯度，将静态的优化⽅法推⼴到函数空间中。

在直接法中，最常⽤的是伪谱的⽅法。伪谱的⽅法是指在正交配置点 处将连续最优控制问题离散化，通过全局差值多项式逼近状态量和输⼊控 制量，直接将最优控制问题转化为⾮线性规划问题，再利⽤⾮线性规划问 题的各种优化⽅法求解。常⽤的伪谱⽅法有Gauss（⾼斯）伪谱法、 Legendre（勒让德）伪谱法、Radau（拉道）伪谱法和Chebyshev（切⽐雪 夫）伪谱法。

最优控制⽅法在那些模型已知的序贯决策问题中已经取得了很好的结 果。若是你⾯对的问题可以⽤精确的模型来描述，便可直接采⽤最优控制 的⽅法。⾄于采⽤最优控制的哪种⽅法，可根据具体问题选⽤。

最优控制经过⼏⼗年的发展，已有很多优秀的成果。在模型未知的强 化学习算法中，这些优秀的成果可直接拿来应⽤。如何应⽤？在基于模型 的强化学习算法中，智能体会先利⽤交互数据拟合⼀个模型，有了模型， 我们就可以利⽤最优控制的计算⽅法计算当前最优解，产⽣当前的最优控 制率。智能体会利⽤当前的最优控制率与环境交互，进⼀步优化⾏为。