最大矩形（单调栈 || 动态规划）

问题描述

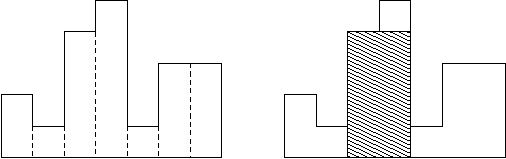
给一个直方图，求直方图中的最大矩形的面积。例如，下面这个图片中直方图的高度从左到右分别是2, 1, 4, 5, 1, 3, 3, 他们的宽都是1，其中最大的矩形是阴影部分。

Input

输入包含多组数据。每组数据用一个整数n来表示直方图中小矩形的个数，你可以假定1 <= n <= 100000. 然后接下来n个整数h1, …, hn, 满足 0 <= hi <= 1000000000. 这些数字表示直方图中从左到右每个小矩形的高度，每个小矩形的宽度为1。 测试数据以0结尾。

Output

对于每组测试数据输出一行一个整数表示答案。

Sample input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample output

8
4000

思考

首先分析一下题目，题目要求得到最大矩形的面积，这个地方类似于木桶原理，一个木桶的容积取决于最短木板，这个矩形的面积也取决于最矮的那个矩形。设当前点高度为 $a[i]$，对于这个点，包含他的最大矩形，是从这个点开始向右找到第一个比他小的节点（设为第 $j$个），向左找到第一个比他小的节点（设为第 $k$个），由于当前点 $i$所在的矩形是区间 $[k+1,j-1]$之间最矮的一个矩形，所以包含这个点的最大矩形面积就是 $((j-1)-(k+1)+1)*a[i]$。

那现在关键在于如何对于每一个节点，向右找到第一个比他小的节点，向左找到第一个比他小的节点。

暴力搜索就别想了，时间复杂度太大，没法做。

从以上分析来看，这个题可以用单调栈来做，也可以使用dp来做。

解题思路–单调栈做法

单调栈介绍

单调栈，故名思义，是一个具有单调属性的栈。单调栈分为单调递增栈（如1 2 3 4）、单调递减栈（如4 3 2 1）、单调非增栈（如4 3 3 1）、单调非减栈（如1 2 2 4）。单调性是从栈底到栈顶还是从栈顶到栈底没有一个明确的规定，我们这里定义为从栈底到栈顶（也就是说，上面这个序列 [1 2 3 4]，4是栈顶元素）。

对于一个数组a[]，单调递增栈的规则如下：

1. 如果 $a[i]>$栈顶元素，则入栈。
2. 如果 $a[i]<=$栈顶元素，将不满足条件的元素弹出， $a[i]$入栈。

比如，我们让 [3 1 2 4 3] 入单调递增栈，步骤如下：

1. 当前元素为3，栈内为空，3入栈。当前栈为 [3] 。（假设栈右边是栈顶）
2. 当前元素为1，栈顶 3>1 ，不满足条件，3弹出，栈内为空，1入栈。当前栈为 [1] 。
3. 当前元素为2，栈顶 1<2 ，满足条件，2入栈。当前栈为 [1 2]。
4. 当前元素为4，栈顶 2<4，满足条件，4入栈。当前栈为 [1 2 4] 。
5. 当前元素为3，栈顶 4>3，不满足，4出栈。新栈顶 2<3 ，满足条件，3入栈。当前栈为 [1 2 3] 。

伪代码如下：

INITIALIZE stack
FOR each element u DO
	WHILE stack.size() > 0 and stack.top() <= u DO
		stack.pop()
	END
	stack.push(u)
END	

单调栈在此题中的应用

我们要求的是当前节点 $i$，向右找比它小的第一个元素，向左找比它小的第一个元素。这样两个元素之间（不包含这两个元素）所有的高度都 $>=a[i]$。

我们采用单调非减栈。对于当前节点 $i$，我们有以下两种情况：

1. 栈顶元素 $>a[i]$，不满足条件的出栈，当前节点入栈。
2. 栈顶元素 $<=a[i]$，节点入栈。

如果是情况1，则对于弹出的所有元素，它们向右找到比它们小的第一个元素都是 $a[i]$（不然也不会弹出）。
如果到了情况2，栈内有元素，那么栈顶元素必定 $<=a[i]$，我们将当前元素的左边第一个比它小的元素定义为栈顶元素。

问题来了，为什么相等还能定义为比它小？这个样子求出的左端点的确有的元素不对，但是，看看下面这个例子：

对于数组 [1 2 2 1] ，此时，第一个2，定义的左端点+1是 $a[2]$，第二个2的左端点+1是 $a[3]$。这样丝毫不影响最终的结果，因为右端点-1都是 $a[3]$，那么第一个2计算的面积 $(3-2+1)*2=4$，一定大于第二个2计算的 $(3-3+1)*2=2$。

当然，你也可以定义两个栈，一个单调非减栈来计算右端点，一个单调非增栈来计算左端点。那样计算出左右端点都没错。这篇博客用的两个栈：传送门

还有一个很细节的地方（我真是太聪明了），将 $a[0]$和 $a[n+1]$都设置为INT_MIN，这样，便于求左端点，同时保证最终栈内没有数组中的元素了。

完整代码–单调栈

//#pragma GCC optimize(2)//比赛禁止使用！
//#pragma G++ optimize(2)
//#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <climits>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;

const int maxn=100000+10;
long long n,a[maxn],L[maxn],R[maxn],st[maxn];
//st数组是单调非减栈，记录的是元素下标，L[i]为第i个元素左边第一个比他小的元素的下标+1，R[i]是第i个元素右边第一个比他小的元素的下标-1
void incstack()
{
    int left=1,right=0;//因为这个样子刚刚好right-left+1=0
    a[0]=INT_MIN;//左端点设置为最小值，便于L数组的查找
    a[n+1]=INT_MIN;//最后一个元素设置为最小值，保证最后栈为空
    for (int i=0; i<=n+1; i++)//注意这里i的取值
    {
        while(left<=right && a[st[right]]>a[i])//单调非减栈
        {
            R[st[right]]=i-1;
            right--;
        }
        st[++right]=i;//入栈，此时栈为单调非减栈
        if(left<=right)//栈不为空，说明此时栈里面里面的下一个元素就是<=它的元素(永远不可能空，因为第一个元素设置为最小值)
        {
            L[st[right]]=st[right-1]+1;//比栈顶元素小(或等于)的是里面的一个元素
        }
    }
}
long long solve()
{
    long long maxx=INT_MIN;
    for (int i=1; i<=n; i++)
    {
        if(((R[i]-L[i]+1)*a[i])>maxx)
            maxx=(R[i]-L[i]+1)*a[i];
    }
    return maxx;
}
long long getlong_long()
{
    long long x=0,s=1;
    char ch=' ';
    while(ch<'0' || ch>'9')
    {
        ch=getchar();
        if(ch=='-') s=-1;
    }
    while(ch>='0' && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*s;
}
int main()
{
    while(n=getlong_long())
    {
        memset(a,0,sizeof(a));
        memset(L,0,sizeof(L));
        memset(R,0,sizeof(R));
        memset(st,0,sizeof(st));

        for (int i=1; i<=n; i++)
            a[i]=getlong_long();

        incstack();//单调非减栈

        long long  ans=solve();

        cout<<ans<<endl;
    }
    return 0;
}

解题思路–动态规划

这个题也可以用dp来做，对于当前点 $a[i]$，定义左边的第一个比它小的元素下标+1存储在 $L[i]$中，右边第一个比它小的元素下标-1存储在 $R[i]$中。也就是说，从 $L[i]$~ $R[i]$之间节点的高度都 $>=a[i]$。

我们先从左到右遍历，如果当前点 $a[i]>a[i-1]$，那么 $L[i]=i-1+1=i$。如果当前点 $a[i]<=a[i-1]$，那么 $L[i]$最少能到 $L[i-1]$。因为从下标 $L[i-1]$到 $i-1$的所有高度都 $>=a[i-1]$。然后我们再用 $a[i]$和 $a[L[i-1]-1]$来比较，依次类推。

从右向左遍历类似。

完整代码–动态规划

//#pragma GCC optimize(2)//比赛禁止使用！
//#pragma G++ optimize(2)
//#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <climits>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;

const int maxn=100000+10;
long long n,a[maxn],L[maxn],R[maxn];

long long getlong_long()
{
    long long x=0,s=1;
    char ch=' ';
    while(ch<'0' || ch>'9')
    {
        ch=getchar();
        if(ch=='-') s=-1;
    }
    while(ch>='0' && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*s;
}
long long solve()
{
    long long maxx=INT_MIN;
    for (int i=1; i<=n; i++)
    {
        if(((R[i]-L[i]+1)*a[i])>maxx)
            maxx=(R[i]-L[i]+1)*a[i];
    }
    return maxx;
}
void dp()
{
    for (int i=1; i<=n; i++)
    {
        int temp=i-1;
        while(a[i]<=a[temp] && temp>=1)
            temp=L[temp]-1;
        L[i]=temp+1;//找到了节点temp，使得a[i]>a[temp]
    }
    for (int i=n; i>=1; i--)
    {
        int temp=i+1;
        while(a[i]<=a[temp] && temp<=n)
            temp=R[temp]+1;
        R[i]=temp-1;//找到了节点temp，使得a[i]>a[temp]
    }
}
int main()
{
    while(n=getlong_long())
    {
        memset(a,0,sizeof(a));
        memset(L,0,sizeof(L));
        memset(R,0,sizeof(R));

        for (int i=1; i<=n; i++)
            a[i]=getlong_long();

        dp();

        long long ans=solve();

        cout<<ans<<endl;
    }
    return 0;
}